4810

	Снова		разделяем переменные		du =	q ( x) dx	и, интегрируя, находим
						v0 (x)
	u = ∫	q ( x)dx
				+ C , где C – произвольная постоянная.
			v (x)
			0
		Подставляя найденные u(x)			и v = v0 ( x)		в функцию (1.14), получаем

		∫	q( x)dx
	решение уравнения (1.13) в виде y =			+
			v0 (x)

C×v0 (x).

Найдем для примера общее решение уравнения

y′ - 2 y = x e2 x

(1.18)

В нем по условию p ( x) = −2 ,

q(x) = xe2 x . Подставив в уравнение y = u × v и

y

′

′

′

u

′

× v + u × v

′

- 2u v = xe

2 x

,

= u

× v + u × v , получим

или

u′ × v + u × (v′ - 2 v) = xe2 x .

(1.19)

В

качестве

функции

v

возьмем одно

решение

v = v0 ( x) уравнения

v′ - 2v = 0 при значении C = 0 . Перепишем его в виде dv = 2v , разделим dx

переменные

dv

= 2dx

и, интегрируя

∫

dv

= 2∫ dx , находим

ln

v

= 2x +C .

v

v

При C = 0 получим

v = v = e2 x .

(1.20)

0

′

2 x

= xe

2 x

du

= x .

Подставим функцию (1.20) в (1.19), получим u e

или

dx

Снова разделяя переменные du = x dx и интегрируя

∫ du = ∫ x dx ,

находим

u =

x2

+ C ,

(1.21)

2

где C – произвольная постоянная.

Подставляя найденные функции (1.20) и (1.21)

в

равенство y = u × v ,

получим общее решение данного уравнения (1.18)

x

2

y =

+ C × e2 x .

2

11

§ 2. Линейные однородные дифференциальные уравнения

второго порядка

Начнём с задачи из механики. Рассмотрим прямолинейное движение материальной точки массы m по оси Ox . Отклонение точки от положения равновесия будем определять функцией x = x(t) . Пусть движение происходит под действием трёх сил: силы, притягивающей точку к началу координат и имеющей проекцию на ось Ox , равную -ax,a > 0 , силы сопротивления среды, которую считаем пропорциональной первой степени скорости -bxɺ,b ³ 0 и возмущающей силы, направленной по оси Ox и

равной F (t) в момент времени t .

Применяя второй закон Ньютона к движущейся массе, получим

mxɺɺ= -bxɺ - ax + F (t) .

Разделим обе части	уравнения			на m и после введения новых
обозначений b / m = 2h ³ 0 ,	a / m = k 2 и F (t) / m = f (t) приведем его к виду
	ɺɺ	ɺ	2	x = f (t) .	(2.1)
	x	+ 2hx + k

Полученное уравнение относится к классу так называемых

линейных дифференциальных уравнений второго порядка, имеющих

вид

y′′ + a1 ( x) y′ + a0 ( x) y = f ( x) .	(2.2)
′	′′
В них неизвестная функция y(x) и ее производные y (x),	y (x)
входят линейно. В качестве коэффициентов уравнения a0 ( x), a1 ( x)	и f ( x)
могут рассматриваться любые функции, непрерывные в интервале	(a, b) .

При этих условиях существует единственное решение уравнения (2.2),

удовлетворяющее заданным начальным условиям

′	, x0 (a, b) .
y(x0 ) = y0 , y (x0 ) = y1
Если правая часть уравнения (2.2) равна нулю:
	y′′ + a1 ( x) y′ + a0 ( x) y = 0 ,	(2.3)

12

то оно называется однородным, в противном случае (если f ( x) ¹ 0 ) –

неоднородным.

Уравнение вида (2.2) служит математической моделью

разнообразных колебательных физических процессов, то есть процессов,

которые характеризуются определенной повторяемостью во времени.

Колебательные процессы широко распространены в природе и технике,

например, качания маятника часов, переменный электрический ток и т.д.

При колебательном движении маятника или груза на пружине изменяется координата центра масс, в случае переменного тока колеблются напряжение и сила тока. Физическая природа колебаний может быть разной, однако они описываются сходными характеристиками и уравнениями одинакового типа. Математические модели, сводящиеся к линейному дифференциальному уравнению второго порядка с постоянными коэффициентами, называют линейным осциллятором.

Методика решений рассматриваемых уравнений базируется на

следующем утверждении.			Если	y1 (x) и	y2 ( x) –	два	каких-либо
непропорциональных		друг	другу	решения	уравнения		(2.3), т.е.
y2 ( x) ¹ λ y1 ( x) ,	то	общее		решение	yoo ( x)	однородного

дифференциального уравнения второго порядка имеет вид

	yoo ( x) = C1 y1 ( x) + C2 y2 ( x) ,
где C1 ,С2 – произвольные постоянные.		Следовательно,	два любых
непропорциональных	решения	однородного	линейного

дифференциального уравнения второго порядка формируют его общее решение. Однако нет общего метода отыскания функций y1 (x) и y2 ( x) . Их легко найти в случае, когда коэффициенты уравнения (2.3) являются числами. Обозначим их a0 и a1 :

		y′′ + a1 y′ + a0 y = 0 .		(2.4)
Такое	уравнение	называется	линейным	однородным
дифференциальным уравнением второго			порядка	с постоянными

13

коэффициентами. Его решения ищут в виде функций y = eλ x . Рассмотрим,

например, уравнение

		y′′ − 3 y′ + 2 y = 0 .
Подставив	в	него функцию	y = eλ x , а также		ее	производные
y′ = (eλx )′ = λ eλx	и	y′′ = (λ eλ x )′ = λ 2 eλ x , получим		eλ x (λ 2 − 3λ + 2) = 0 .
Поскольку eλx ¹ 0,		функция y = eλ x	будет решением,		если	λ – корень
квадратного уравнения
		λ 2 − 3λ + 2 = 0 ,

которое называют характеристическим уравнением соответствующего

дифференциального уравнения. Его корни							λ1 = 1		и	λ2 = 2 , поэтому
непропорциональные функции	y		= e x		и	y	2	= e2 x	формируют		общее
	1
решение этого уравнения	y	oo		= C	e x + C			e2 x .	В	общем	виде
				1			2

характеристическое уравнение дифференциального уравнения (2.4) имеет вид

λ 2 + a	λ + a	0	= 0 .	(2.5)
1

Если

a 2

/ 4 − a

0

> 0 ,

то

уравнение (2.5)

имеет два

различных

1

действительных корня

λ1 и λ2 , которые определяются формулой

λ

= −

a

±

a

2

− a .

1

1

1,2

2

4

0

При

этом

непропорциональные

решения

уравнения

y = eλ1 x

и

1

y

2

= eλ 2 x формируют общее решение уравнения (2.4) в виде

y

oo

( x) = C

eλ1 x + C

2

eλ 2 x .

1

Рассмотрим дифференциальное

уравнение

y′′ − 4 y′ + 4 y = 0 . Его

характеристическое уравнение имеет два одинаковых корня λ1 = λ2 = 2 (в

таком случае говорят, что λ1 – корень кратности два). Одно из решений в этом случае нам известно: y1 = e2 x . Непосредственной подстановкой в

14

уравнение можно убедиться, что функция y2 = xe2 x также будет решением

этого уравнения. Поскольку полученные функции непропорциональны,

общее решение

дифференциального

уравнения

получается

в

виде

y

oo

= C

e

2x + C

2

xe2 x .

1

В

целом

можно сказать, что если

выполняется

условие

a

2

/ 4 − a

= 0 ,

то

характеристическое

уравнение

(2.5)

имеет

кратный

1

0

корень

λ = −a1 / 2 ,

а

общее

решение

yoo (x)

однородного

дифференциального

уравнения

второго

порядка

имеет

вид

y

oo

= C

e

λ x + C

2

xe

λ x = (C

1

+ C

2

x)e−a1 x / 2 .

1

Если же характеристическое уравнение (2.5) имеет комплексные

корни λ

1,2

= α ± β i , то можно убедиться, что функции y

= eα x

cos β x и

1

y2 = eα x sin β x

образуют пару непропорциональных решений уравнения

(2.4), а его общее решение имеет вид

yoo ( x) = eα x (C1 cos β x + C2 sin β x) .

	Такая ситуация возникает, если a 2 / 4 − a < 0 , при этом α							= −a / 2 ,
					1	0		1
β =
	a	− a 2	/ 4 .
0		1
	Рассмотрим, например, дифференциальное						уравнение y′′ + 4 y = 0 .
Его характеристическое уравнение					λ 2 + 4 = 0	имеет комплексные корни
λ1,2 = ±2i ,			а общее решение,		тем самым, приобретает вид
yoo ( x) = C1 cos 2 x + C2 sin 2 x . Для					уравнения		y′′ + 2 y′ + 5 y = 0	также

составим характеристическое уравнение: λ 2 + 2λ + 5 = 0 . Его комплексные

корни λ1,2 = −1 ± 2i позволяют записать общее решение

дифференциального уравнения в виде yoo ( x) = e− x (C1 cos 2 x + C2 sin 2 x) .

Вернёмся теперь к механическим колебаниям. Отсутствию

возмущающей силы соответствует уравнение (2.1), в котором				f (t) = 0 :
ɺɺ	ɺ	2	x = 0 .	(2.6)
x	+ 2hx + k

15

Такое уравнение называется уравнением свободных колебаний.

Характеристическое уравнение в этом случае имеет вид

							λ 2 + 2hλ + k 2 = 0 .	(2.7)
Свободные			колебания				в среде без сопротивления описываются
уравнением	ɺɺ	+ k		2	x = 0 .	В этом случае характеристическое уравнение
	x
λ 2 + k 2 = 0	имеет		мнимые				корни λ = ±ik , ему соответствует	общее

решение

xoo = C1 cos kt + C2 sin kt.

Удобно привести записанное решение к другой форме, введя новые обозначения. Умножив и разделив на С12 + С22 , получим

					C1					C2
2		2
xoo = C1								coskt +
		+ C2			C2	+ C2				C2	+ C2		sin kt	.
					1	2				1	2

Если положить

C1

= sinϕ,

C2

= cosϕ ,

C 2

+ C 2

= A,

+ C 2

+ C 2

1

2

C 2

C2

1

2

1

2

то общее решение приобретает вид

xoo = A(sinϕcoskt + cosϕsinkt) = Asin(kt +ϕ).

Оно описывает движение, которое называют гармоническим колебанием. Его график имеет вид:

положенияравновесия

время

отклонение от

16

Величину A называют амплитудой колебания, аргумент kt + ϕ —

фазой колебания, величину ϕ - начальной фазой колебания. Величина k

представляет собой частоту колебания. Напомним, что k = 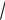a / m . Период колебания T = 2π / k = 2π 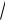m / a и частота k зависят только от массы

системы и силы, притягивающей точку к началу координат. В задаче о движении тела, подвешенного на пружине, это означает зависимость от

жесткости пружины.
	Свободные колебания в среде с сопротивлением описываются
уравнением		(2.6).		Если	h2 − k 2 > 0 (h > k ) ,	то	характеристическое
уравнение		(2.7)		имеет	два различных	действительных корня
λ	= −h ±
		h2 − k 2		. В модели движения груза		на	пружинке указанное
1,2
условие означает,				что сила сопротивления среды		больше силы упругости

пружины. Общее решение дифференциального уравнения в этом случае

xoo (t) = C1e(− h+ h2 −k 2 ) t + C2e( − h− h2 −k 2 )t описывает апериодическое движение.

Поскольку корни характеристического уравнения отрицательны, то с

ростом t координата x = x(t) стремится к нулю.

Характеристическое уравнение (2.7) имеет кратный корень λ = −h ,

если h2 = k 2 , то есть h = k . Для задачи о движении груза на пружине это

означает, что сила сопротивления и сила упругости пружины

«уравновешены» в смысле указанного равенства. Общее решение

приобретает вид x		oo	(t) = (C	1	+ C	2	t)e− ht	. При малых значениях	t	основную
«роль» играет первый множитель, линейный относительно									t ,	а затем с
увеличением	t		материальная точка будет стремиться к положению
равновесия.
Если же	h2 − k 2 < 0				(то есть			h < k - упругая сила		пружины

превосходит силу сопротивления среды в задаче о грузе на пружине), то характеристическое уравнение (2.7) имеет комплексные корни

λ	= −h ± k 2 − h2 i .
1,2

17

Общее решение
xoo (t) = e− ht (C1 cos k 2 − h2 t + C2 sin k 2 − h2 t) = Ae−ht sin(								k 2 − h2 t + ϕ )
описывает	затухающие		гармонические			колебания		с	периодом
T = 2π / k 2 − h2 ,		частотой	k 2 − h2 и амплитудой				Ae− ht ,	убывающей с
увеличением	t . Вид графика решения:
отклонение									время
Проанализировав полученные результаты, можно сказать, что
наличие сопротивления (h > 0)				видоизменяет характер колебаний: пока
сопротивление		сравнительно		невелико		(h < k ) ,	движения		остаются
периодическими, затухая с увеличением					t , при большом сопротивлении
среды (h ³ k ) движения становятся апериодическими.

18

yчн ( x)

§3. Линейные неоднородные дифференциальные уравнения

второго порядка с постоянными коэффициентами

Методика решения неоднородных линейных дифференциальных

уравнений базируется на теореме о том, что общее решение yoн ( x)

неоднородного линейного уравнения равно сумме общего решения yoo ( x)

соответствующего ему однородного уравнения и какого-либо частного

решения неоднородного уравнения, то есть

yoн ( x) = yoo ( x) + yчн ( x) . Поскольку алгоритм нахождения общего решения однородных уравнений был изложен, остается рассмотреть способ

получения второго слагаемого - частного решения yчн ( x) .
Будем		рассматривать			правую		часть	f ( x) уравнения	(2.2) в
специальном виде
f ( x) = Q ( x)eα x cos β x					или		f ( x) = Q ( x)eα x sin β x ,
	n							n
где Q ( x) = q	n	xn + q	n−1	xn−1 + …+ q x + q			– заданный многочлен степени n .
n					1	0
Назовем параметром таких функций комплексное число γ = α + iβ .
Прежде чем решать неоднородное уравнение со специальной правой
частью, нужно сравнить параметр						γ = α + iβ		функции из правой части с

корнями характеристического уравнения, соответствующего однородному уравнению. Для описания этого совпадения введем число k . Если

параметр γ	не совпадает ни с одним из корней характеристического
уравнения,	то считаем k = 0 . При совпадении γ с корнем

характеристического уравнения считаем k равным кратности совпавшего корня в характеристическом уравнении (для уравнений второго порядка кратность может принимать значения 1 или 2 ).

Далее в зависимости от степени n многочлена и конкретного значения параметра γ функции в правой части неоднородного уравнения,

можно записать вид, который имеет частное решение yчн ( x) .

19

			Начнем с рассмотрения		функции f ( x) = Q ( x)eα x			(параметр γ
						n
имеет			действительное	значение, поскольку		β = 0).	В	этом случае
y	чн	( x) = xk P ( x)eα x , то		есть	частное решение	ищут	в	виде функции
			n

специального вида с тем же параметром и той же степени, что и в правой

части, умножая	ее на	xk . При этом,		как отмечалось, возможны			три
варианта: k = 0 ,	k = 1	или	k = 2. Конкретные		числовые значения
коэффициентов	многочлена		P ( x) = p xn + p			xn−1 + …+ p x + p
			n	n	n−1	1	0

необходимо определять, подставляя в исходное уравнение функцию, в

виде которой записано частное решение.

Рассмотрим, например, неоднородное уравнение

y′′ − 3 y′ + 2 y = 4 xe3 x .

Функция в его правой части

f ( x) = 4 xe3 x

имеет степень n =1 и параметр

γ = 3, не совпадающий с корнями

λ1 = 1 и λ2 = 2 характеристического

уравнения,

то есть

k = 0 .

Поэтому частное решение такого уравнения

имеет вид

y

чн

( x) = x0 P ( x)e3 x

= ( p x

+ p )e3 x . Для определения числового

1

1

0

значения коэффициентов

p0

и

p1 найдем

производные функции

указанного

вида

(( p1 x + p0 )e

3 x

′

= p1e

3 x

+ (3 p1 x + 3 p0 )e

3 x

,

)

(( p1 x + p0 )e

3 x ′′

3 x

+ (9 p1 x + 9 p0 )e

3 x

и подставим в уравнение:

)

= 6 p1e

(6 p

+ 9 p x +

9 p

− 3 p − 9 p x

− 9 p

+ 2 p x

+ 2 p )e3 x = 4 xe3 x .

1

1

0

1

1

0

1

0

Полученное после сокращений равенство 3 p1 + 2 p1 x + 2 p0 = 4 x обратится

в тождество, если приравнять коэффициенты при соответствующих

степенях переменной x в его обеих частях: 2 p1 = 4 и 3 p1 + 2 p0 = 0 . Тем

самым,			p0 = −3			и	p1 = 2 дают нужные значения коэффициентов для
частного решения: y							чн	( x) = (2 x − 3)e3 x . С учетом найденного ранее общего
решения						однородного			уравнения,	получаем
y	oн	( x) = C		e x + C	2	e2 x	+ (2 x − 3)e3 x .
			1

20