5132

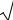
Теорема. Если				функция			z = f (x, y) дифференцируема в			точке
M (х0 , у0 ) , то есть имеет вид (1), то она непрерывна в этой точке и
									∂z	∂z
имеет в ней частные производные по каждому аргументу									¶x	и ¶y ,
причем ¶z			= А, ∂z			= В.
¶x		M	∂y			M
В силу теоремы, равенство (1) можно записать в виде
			Dz = ∂z × Dx + ∂z × Dy + α × Dx + β × Dy .							(2)
						¶x	¶y
			4. Дифференцирование сложных функций
Пусть задана функция z = f (x, y) , где переменные x и y ,										в свою
очередь,			являются			функциями		независимой	переменной
t : x = x(t), y = y(t)				Тогда функция				z = f [x(t), y(t)] будет сложной

функцией независимой переменной t , а переменные x и y будут для нее

промежуточными переменными.

Теорема. Если функции x = x(t) и y = y(t) дифференцируемы в

точке t , а функция z = f (x, y) дифференцируема в точке M (x(t); y(t)),

то сложная функция z = f [x(t), y(t)] также дифференцируема в точке

t , причем

dz

=

∂z ×

dx

+ ∂z ×

dy

.

(1)

dt

dt

dt

¶x

¶y

dz

, где z = cos

x

,

x = 2t + t 2 , y =

Пример. Найти

t .

dt

y

Решение. Найдем сначала

∂z ,

∂z ,

dx

,

dy

:

¶x

¶y

dt

dt

10

∂z

= (-sin

x 1

∂z

= (-sin

x

x

)

¶x

y ) × y

,

¶y

y ) × (- y 2

,

	dx	= 2 + 2t ,	dy	=	1		.
	dt		dt 2 t
Тогда, согласно формуле (1), имеем

	- sin
=

		2t + t 2
=	- sin
			t

dz

=

∂z ×

dx

+

∂z ×

dy

=

dt

¶x

dt

¶y

dt

x

1

x

x

1

×

× (2

+ 2t) +

- sin

×

-

×

=

2

y

y y

y

2 t

1

2t + t 2

2t + t 2

1

×

× (2 +

2t) +

- sin

×

-

×

=

t

t

t

2 t

2t + t 2

1

(1 +1,5t ).

=

- sin

×

×

t

t

5. Дифференцирование неявных функций
Пусть уравнение
F (x, y, z) = 0	(1)

определяет z = f (x, y) как некоторую дифференцируемую функцию двух переменных.

Найдем частные производные				∂z	и		∂z	неявной функции			z ,
				¶х			¶y
заданной уравнением (1). Для этого,				подставив в уравнение						вместо	z
функцию f (x, y) , получим тождество					F (x, y, f (x, y)) ≡ 0 .					Частные
производные по x и по y функции,				тождественно равной нулю, также
равны нулю:
	∂		F (x, y, f (x, y)) =	∂F +		∂F ×		∂z = 0 ,
	¶x			¶x			¶z	¶x
	∂			∂F	+	∂F		∂z
	¶y F (x, y, f (x, y)) =			¶y			¶z ×	¶y = 0	.

11

Откуда

¶z

= -

Fx/

¶z

= -

Fy/

/

¹ 0 ).

¶х

и

¶y

( Fz

(2)

Fz/

Fz/

Пример. Найти

∂z ,

∂z , где

e z

+ z - x 2 y +1 = 0 .

¶x

¶y

Решение. Здесь F (x, y, z) = e z + z - x 2 y +1,

F /

= -2xy

, F /

= -x 2 , F / = e z +1.

x

y

z

Тогда по формуле (2) имеем:

∂z =

2xy

,

¶z =

x 2

.

¶x e z +1

¶y e z +1

6. Касательная плоскость и нормаль к поверхности

Пусть функция

z = f (x, y) ,

дифференцируемая в точке (х0 , у0 ) ,

задает в пространстве

поверхность

S .

Пересечем

эту

поверхность

плоскостями

х = х0 и

у = у0

(см. рис. 6).

Плоскость

х = х0 пересекает

поверхность

S

по

некоторой

линии

z0 ( y) , уравнение которой

получается подстановкой в выражение исходной функции

z = f (x, y)

вместо x числа

х0 .

Точка М0 (х0 , у0 , f (x0 , y0 ))принадлежит кривой

z0 ( y) .

Рис. 6

12

В силу	дифференцируемости функции z = f (x, y)	в точке М0
функция	z0 ( y) также является дифференцируемой в	точке	у = у0 .
Следовательно, в этой точке плоскости х = х0 к кривой		z0 ( y)	может

быть проведена касательная l1 . Проводя аналогичные рассуждения для

сечения у = у0 , построим касательную l2 к кривой z0 (x) в точке

х = х0 . Прямые l1 и l2 определяют плоскость α , которая называется

касательной плоскостью к поверхности S в точке М0 .

Прямая, проходящая через точку М0 (х0 , у0 , z0 ) и перпендикулярная

касательной плоскости, построенной в этой точке поверхности,

называется нормалью к поверхности в точке М0 (х0 , у0 , z0 ) .

Теорема. Если функция z = f (x, y) дифференцируема в точке

(х0 , у0 ) , то касательная плоскость к поверхности, заданной уравнением z = f (x, y) , в точке М0 (х0 , у0 , z0 ) определяется уравнением

z - z0

= f x/ (x0 , y0 ) × (x - x0 ) + f y/ (x0 , y0 ) × ( y - y0 ) ,

(1)

а нормаль к этой поверхности в заданной точке имеет уравнение

x − x0

=

y − y0

=

z − z0

.

(2)

f x/ (x0 , y0 )

f y/ (x0 , y0 )

−1

Если

поверхность

задана

неявно

уравнением F (x, y, z) = 0

и

функция F (x, y, z) дифференцируема

в

точке М0 (х0 , у0 , z0 ) ,

то

касательная

плоскость

к этой

поверхности

в точке

М0 (х0 , у0 , z0 )

определяется уравнением

F /

× (x - x

0

) + F /

× ( y - y

0

) + F

/

× (z - z

0

) = 0,

(3)

x

M 0

y

M 0

z

M 0

а нормаль к этой поверхности в заданной точке имеет уравнение

13

x − x0

y − y0

z − z0

F /

=

F /

=

F /

.

(4)

x

M 0

y

M 0

z

M 0

Замечание. Формулы касательной плоскости и нормали к поверхности получены для обыкновенных, то есть не особых точек поверхности. Точка М0 поверхности называется особой, если в этой точке все частные производные равны нулю или хотя бы одна из них не существует. Такие точки мы не рассматриваем.

Пример. Составить уравнение касательной плоскости и нормали к поверхности: а) z = x 2 + y 2 в точке М0 (1,−1, 2) , б) x2 − 4 y2 + 2z2 = 6 в

точке М0 (2, 2, 3) .

Решение. а) Поверхность задана явно, поэтому воспользуемся формулами (1), (2). Здесь

f x/ = 2x , f x/ (1,-1,2) = 2 ×1 = 2,

f y/ = 2 y , f y/ (1,-1,2) = 2 × (-1) = -2 .

Тогда искомое уравнение касательной плоскости имеет вид:

z- 2 = 2 × (x -1) + (-2) × ( y - (-1)) или 2x − 2 y − z − 2 = 0

иуравнение нормали:

x −1			y + 1			z − 2
		=			=		.
2			- 2			-1

б) Поверхность задана неявно, поэтому воспользуемся формулами

(3), (4). Здесь

F (x, y, z) = x 2 - 4 y 2 + 2z 2 - 6 ,

Fx/ = 2x , Fx/ (2,2,3) = 2 × 2 = 4 ,

Fy/ = -8 y , Fy/ (2,2,3) = -8 × 2 = -16 ,

Fz/ = 4z , Fz/ (2,2,3) = 4 × 3 = 12 .

Тогда искомое уравнение касательной плоскости имеет вид:

14

4 × (x - 2) + (-16) × ( y - 2) +12 × (z - 3) = 0

или

x − 4 y + 3z − 3 = 0

и уравнение нормали: x − 2 = y − 2 = z − 3 .

4 -16 12

7. Полный дифференциал функции двух переменных и его геометрический смысл

Дифференциалом dz дифференцируемой в точке (х0 , у0 )

функции	z = f (x, y)	называется главная				линейная, относительно
приращений независимых переменных					x	и	y ,	часть	полного
приращения этой функции в точке (х0 , у0 ) , то есть
		dz =	∂z		∂z
			¶х × Dх +		¶y × Dу				(1)
						.
Если	положить	z = х,	то	dz = dx = 1× Dх + 0 × Dу = Dx ,					то есть
dx = Dx .	Аналогично,	полагая		z = у ,	получим,		что	dу = Dу.	Таким

образом, дифференциалы независимых переменных совпадают с приращениями этих переменных, то есть

∂z	∂z
dz = ¶х × dх +	¶y × dу	(2)
	.
Геометрический смысл дифференциала: если полное приращение
функции z представляет геометрически приращение		AC аппликаты

поверхности z = f (x, y) , то дифференциал функции dz есть приращение

AB аппликаты касательной плоскости к поверхности z = f (x, y)	в
данной точке, когда переменные x и y получают приращения x и	y
(см. рис.7).

15

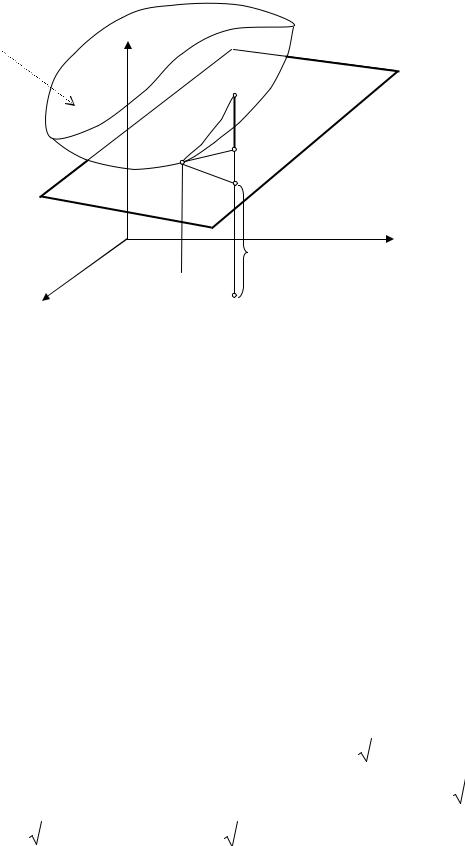
z = f ( x, y)

M ( x, y, z)

M	N ( x, y, Z )
	0
	P( x, y, z	0 )	MP = z
			NP = dz

z0

(x 0 , y 0 )

( x, y)

Рис. 7

Напомним, что если функция z = f ( x, y) дифференцируема в точке

(х0 , у0 ) , то ее полное приращение в этой точке может быть представлено в виде

Dz =

∂z

(x , y

) × Dx +

∂z

(x , y

) × Dy + α (Dх, Dу) × Dx + β (Dx, Dy) × Dy

(3)

0

0

¶x

0

¶y

0

Из соотношений (2) и (3) следует, что при достаточно малых |

x | и

|

y |

имеет место приближенное равенство

z ≈ dz . Отсюда получаем

формулу для приближенных вычислений:

f (x

+ Dх, y

+ Dу) » f (x , y ) + f /

(x , y ) ×Dx + f / (x , y ) ×Dy

(4)

0

0

0

0

x

0

0

y

0 0

Пример. Вычислить приближенно ln(1,98 -

).

1,01

f (x, y) = ln(x −

).

Решение.

Рассмотрим

функцию

y

Тогда

ln(1,98 −

) = ln((x0 +

x) −

),

x0 = 2,

x = −0,02, .

1,01

y0 +

y

где

y0

= 1,

Dy = 0,01. Воспользуемся формулой (4),

предварительно найдя

f /

и

f

/

:

x

y

16

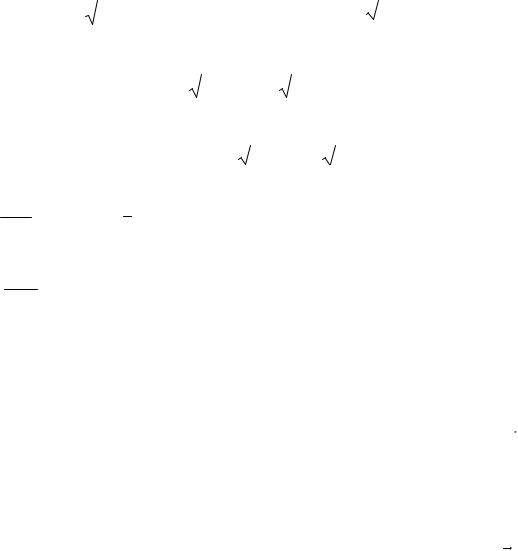
f x/	=	1			,		f x/ ( x0 , y0							) = f x/ (2,1) =															1							= 1 ,
		x −																										2 -
																																		1
			y
			/					1												1
					f y	=		x -		y				×	-					×							,
															2								y
/						/								1									1
f y	(x0 , y0 ) = f y						(2,1)		=										×		-												= -0,5 .
														-									2 ×
															1
									2																			1

Следовательно,

ln(1,98 − 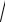1,01) ≈ ln(2 - 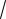1)+ 1× (-0,02) + (-0,5) × 0,01 = -0,025 .

Для сравнения: используя микрокалькулятор, находим:

ln(1,98 - 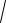1,01) » -0,025305051.

8. Производная по направлению. Градиент

Пусть в области D , в которой определена функция z = f (x, y) , в

некоторой внутренней точке M 0 (x0 , y0 ) задано направление вектором l

(см. рис. 8). Нас интересует поведение функции при движении точки

M (x, y)		в этом направлении. Пусть t расстояние между точками M 0 и
M , а	e			единичный вектор заданного направления l .
		= cosα i + sin α j –
Тогда		координаты	точки		M (x, y)	равны:	x = x0 + t cosα ,
y = y0	+ t sin α . Если точка			M	стремится к точке		M 0 по заданному

направлению, то t → 0.

17

y
	l

M (x, y )

D

e

α

M0 ( x0 , y0 )

x

Рис. 8

Производной функции

z = f (x, y)

в точке M 0 (x0 , y0 ) в заданном

направлении l называется предел

lim

f (x

0

+ t cosα , y

0

+ t sin α )− f (x

0,

y

0

)

=

df

.

t

t→0

d l

∂ z

∂ z

В частности,

частные производные

∂ x ;

это производные по

∂ y

положительному направлению координатных осей Ox и Oy

соответственно. Оказывается, что для функции, имеющей непрерывные частные производные, производная по направлению выражается через частные производные в данной точке. Чтобы это доказать, нам необходимо научиться находить частные производные сложных функций.

	Производная			∂ z	характеризует скорость			изменения функции в
				∂ l
	направлении l .
	Теорема. Если функция						z = f (x, y) дифференцируема		в точке
	(х0 , у0 ) , то производная					∂ z	по направлению	l = {cos α ,	sin α } в
						∂ l
	точке (х0 , у0 ) определяется формулой
		∂z	( x0 , y0 ) =	f x/ ( x0 , y0 ) × cos α + f y/ ( x0 , y0 ) × sin α ,					(1)
		¶l

18

где e = {cos α , sin α} – единичный вектор заданного направления l .

Замечание.

Если направление l задано вектором a = {a1 , a2 } , то

производная

∂z

функции

z = f (x, y)

по направлению l может быть

¶l

подсчитана по формуле

∂z

/

a1

/

a

2

( x0 , y0 ) = f x

( x0 , y0 ) ×

+

f y ( x0

, y0 ) ×

.

(2)

a12 + a22

a12

+ a22

¶l

Пример. Найти производную от функции

z = 3x4 − xy + y3

в точке

М(1,2) в направлении, составляющим с осью Ox угол в 600 .

Решение. Направление задано углом наклона к оси Ox , поэтому воспользуемся формулой (1).

f x/ =12x3 - y ,	f x/ (x0 , y0 ) = f x/ (1,2) = 12 ×13 - 2 = 10 ,
f y/ = − x + 3 y 2 ,	f y/ ( x0 , y0 ) = f y/ (1,2) = -1 + 3 × 2 2 = 11 ,
∂z (1,2) = 10 × cos 60	+11× sin 60 = 10 × 0,5 +11× 0,5		= 5 + 5,5
		3		3.
¶l

Пример. Найти производную от функции z = ln( x 2 + 2 y) в точке

М(1;2) по направлению вектора a = 3i − 4 j .

Решение. Направление задано координатами вектора a , поэтому воспользуемся формулой (2).

f x/ =			2x				f x/ ( x0 , y0 )
						,
			x2 + 2 y
f y/ =			2		,		f y/ ( x 0 , y 0 )
	x	2	+
				2 y

= f x/ (1,2) =					2 ×1		= 0,4 ,
			12		+ 2 × 2
=	/	(1,2 )	=		2			= 0 , 4
	f y								,
						12 + 2 × 2

∂ z	(1,2 ) = 0 ,4 ×		3		+ 0 ,4 ×			− 4		= - 0 ,08 .
¶ a
			3 2 + ( - 4 ) 2					+ ( - 4 ) 2
				3 2

Рассмотрим понятие градиента функции z = f (x, y) .

19