8066

∙изгибающие моменты от моментной нагрузки будут положительными, если сосредоточенные моменты М действуют по часовой стрелке при размещении начала координат на левом конце балки;

∙при размещении начала координат на правом конце балки сосредоточенный момент М необходимо вводить в уравнение со знаком «плюс», если он действует против часовой стрелки.

8.Универсальное уравнение углов поворота сечений балки получается из уравнения (1.14) путём его дифференцирования: EJxθ(z) = EJxv′ (z).

1.2.3 Примеры решения балок методом начальных параметров.

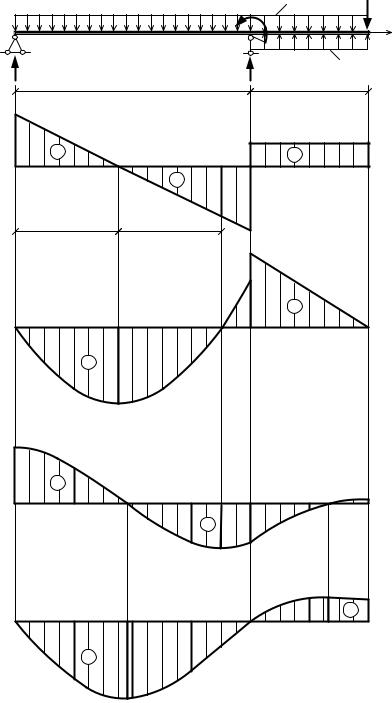
Пример 1. Для балки определить углы поворота сечений и прогибы методом начальных параметров.

Начало координат помещаем на левом конце балки, ось у направим вниз (рис. 1.12).

Начальные параметры: vo = vA = 0, θo = θA ≠ 0, Mo = 0, Qo = 70 кН.

Универсальное уравнение прогибов балки:

EJx v (z) = EJx		z3		z4		(z - 4)4		(z - 4)2		(z - 4)3
	θo z - 70		- 40		+ 40		- 20		+ 120		.
		6		24
					24		2		6

Примечание: при различных значениях Z значения в круглых скобках всегда неотрицательные числа, в противном случае отрицательное слагаемое в рассматриваемом выражении не учитывается – оно равно нулю.

Условия закрепления балки.	При z = 0				vA = vo = 0.
При z = 4 м v(4) = vВ = 0:
	43		44
EJx v (4) = EJxθo ×4 - 70		- 40			= 0. Отсюда находим EJxθo = 80,00.
	6		24

Уравнение прогибов балки окончательно примет вид:

EJxv (z) = 80,0 z - (35 / 3) z3 + (5 / 3) z4 - (5 / 3)(z - 4)4 + 10(z - 4)2 - 20(z - 4)3 .

Дифференцируя уравнение прогибов, получим уравнение углов поворота:

EJxθ (z) = 80, 0 - 35 z2 + (20 / 3) z3 - (20 / 3)(z - 4)3 + 20 (z - 4) - 60 (z - 4)2 .

Вычисляем углы поворота и прогибы в сечениях балки.

z(м)	0	1	2	3	4	5	6
EJxθ(z)	80,00	51,67	-6,67	-55,00	-53,33	-8,33	6,67
EJxv(z)	0	70.00	93.33	60.00	0	-28.33	-26.66

	q=40кН/м	М=20кНм	q	F=30кН
				z
RA=70кН			RB=120кН	q
	4 м
			2 м
70,00	эп.Qy (кН)
+		30,00	+	30,00
		-
1,75 м		1,75 м
			90.00
	эп.Мх (кНм)		60,00
		40,00
			-
+
	61,25
80,00
51,67	эп. EJx
+	6,67		8,33	6,67
		-
		55,00	53,33
	эп. EJxV		28,33	26,66
				-
+
		60,00
70,00
	93,33
		Рис. 1.12

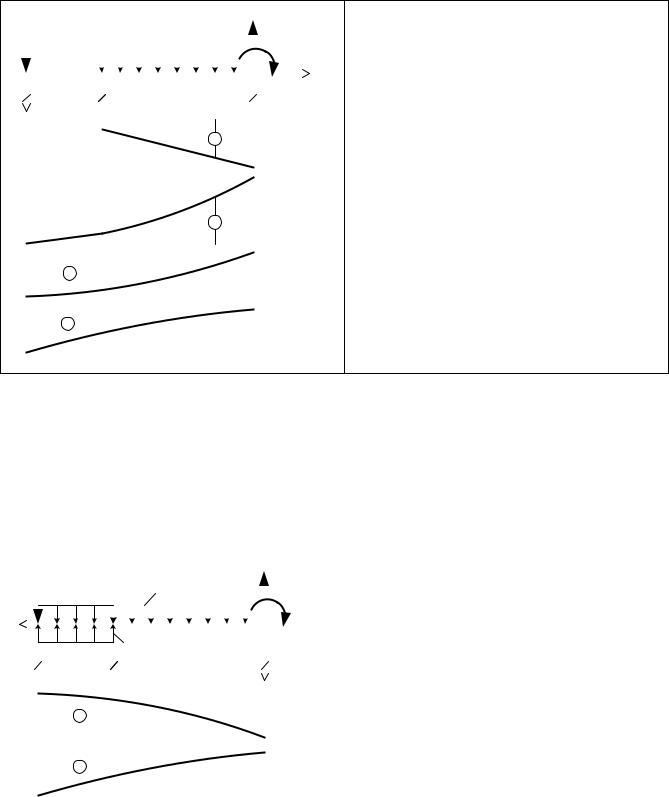
Пример 2. Определить углы поворота сечений и прогибы консоли.

I.Начало координат помещаем на левом конце консоли (рис. 1.13). Ось у направляем вниз.

RB = 30 кН

		F = 6 кН													q = 12					кН/м								МB = 42 кНм
																													z
				1 м													2 м
6		y																										эп.Qy (кН)
																							-
	6																											30
	6																						-					42
																												эп.Мх (кНм)
43						-																						эп EJx
						40
						+																						эп.EJxv
94							52

Рис. 1.13

Начальные параметры балки:

vo ¹ 0 , θo ¹ 0 , Mo = 0 , Qo = - 6 кН.

Универсальное уравнение прогибов балки:

	EJxv (z) = EJxvo		z3		(z − 1)4
		+ EJxθo z − − 6		− 12		=
			6
					24

= EJxvo + EJxθo z + z3 + 0,5(z − 1)4 .

Уравнение углов поворота сечений балки:

EJxθ (z) = EJxθo + 3z2 + 2(z − 1)3 .

Условия закрепления балки.

При z = 3м: EJxθ(3) = θ(3) = θB = 0, EJxθo + 3٠32 + 2 (3-1)3 = 0.

Отсюда находим: EJxθo = - 43.

При z = 3м: EJxv(3) = v(3) = vB = 0,

EJxvo – 43 ٠3 + 33 + 0,5 (3-1)4 = 0.

Отсюда находим: EJxvo = 94.

Окончательно универсальные уравнения углов поворота и прогибов балки имеют следующий вид:

EJxθ(z) = - 43 + 3z2 + 2(z-1)3 . EJxv(z) = 94 – 43z + z 3 + 0,5(z-1)4 .

Эпюры перемещений показаны на рис. 1.13.

II. Начало координат помещаем на правом конце консоли (рис. 1.14). Ось у направляем вниз.

RB = 30 кН

Начальные параметры балки:

F = 6 кН

q = 12 кН/м

МB = 42 кНм

vo = 0 , θo = 0 ,

Mo = - 42кНм ,

Qo = 30кН.

Универсальное уравнение прогибов балки:

z

(z − 2)4

z2

z3

z4

q

EJxv (z) = − − 42

+ 30

− 12

+

12

=

1 м

2 м

2

6

24

24

y

= 21z2 − 5z3 + 0,5z4 − 0,5(z − 2)4 .

43

40

+

эп EJx

Уравнение углов поворота балки:

EJxθ (z) = 42 z − 15z2 + 2z3 − 2(z − 2)3 .

Угол поворота и прогиб левого конца кон-

+

эп.EJxv

соли при z = 3 м:

94

52

EJxθ(3) = 42٠3 – 15 ٠32 + 2٠33

-2٠(3-2)3

= 43.

Рис. 1.14

EJxv(3) =

= 21٠32 – 5 ٠33 + 0,5٠34 - 0,5٠(3-2)4 = 94.

Эпюры перемещений показаны на рис. 1.14.

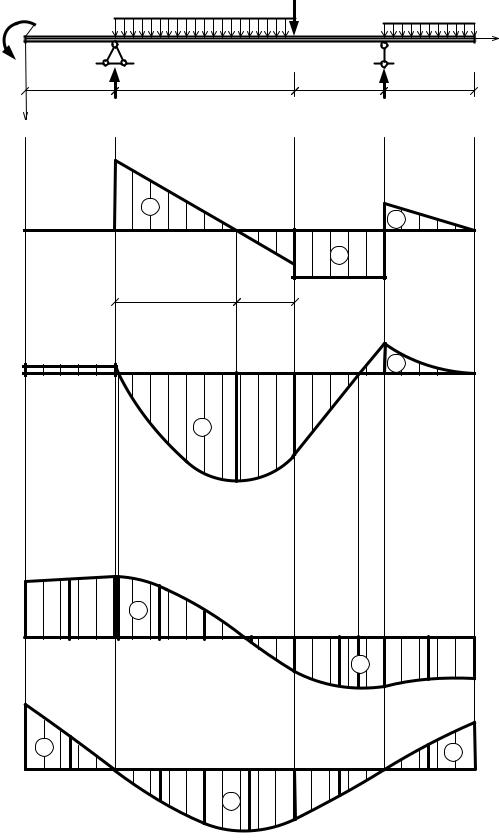
Пример 3. Подобрать сечение балки (рис.1.15) из прокатного двутавра Расчётные характеристики балки: [ σ ] = 160 МПа, [ τ ] = 100 МПа, Е = 2·105 МПа.

Допускаемый прогиб балки в пролёте: [ f ] = l / 200.

1. Строим эпюры Qy, Mx и определяем номер двутавра из условий прочности.

	M		8200кНсм
Wx ³	x	=		= 512,5 см3 .
	[σ ]		16 кН / см2

Из таблицы 1. Сталь горячекатанная. Балки двутавровые (ГОСТ 8239-72*), находим следующий номер профиля:

двутавр №30а: Wx = 518 см3, Jx = 7780 см4, Sx = 292 см3, d = 0,65 см.

Выполняем проверку балки на срез:

τ =	Qy Sx	=	65кН ×292см3	= 3,75	кН	= 37,5МПа < [τ ] = 100МПа.
			7780см4 × 0,65см		см2
	Jx d

Жёсткость балки при изгибе равна: EJx = 2×104 × 7780 кНсм2 = 15560 кНм2.

2. Определяем перемещения балки.

Начало координат помещаем на левом конце балки. Ось у направляем вниз. Начальные параметры балки: vo = ?, θо = ?, Mo = - 6 кНм, Qo = 0.

Универсальное уравнение прогибов заданной балки имеет вид:

		6z		2		6	(z −	2 3			2	(z −	2 4		2	(z −	6 4			1	(z −	6 3		6	(z −
				2		5		)			4		)		4		)			2		)		7
EJ x v = EJ x v o + EJ x θ o z −	−				+		6			−		2		+		2			−		6		+		6
												4				4

8 3

)

18 4

2(z − )

−2

4

.

Неизвестные начальные параметры определяем из условий закрепления балки:

при z = 2 м: vA = 0,	EJvo	+ EJθo	×2 + 6	22			= 0.
			2
при z = 8 м: vB = 0,	EJvo	+ EJθo	×8 + 6		82			- 65	(8 - 2)3	+ 24	(8 - 2)4	- 24	(8 - 6)4	+ 12	(8 - 6)3	= 0
			2				6			24		24		6

Решая систему уравнений, находим неизвестные начальные параметры, которые будут рав-

ны: EJхθo = 144, EJхvo = - 300.

Углы поворота и прогибы определяются следующими выражениями:

EJv(z) = - 300 + 144z + 3z2 - 65/ 6(z - 2)3 + (z - 2)4 - (z - 6)4 + 2(z - 6)3 - 67 / 6(z - 8)3 +1/2(z - 8)4

	1		6	6	2	2	2	4	2	3		4	6	3	6	6	2	6	2	8	2		2	8 3
EJθ (z) = 4 +			z −	5 /	(z −	)	+	(z −	)		−	(z −	)	+	(z −	)	−	7 /	(z −	)	+		(z −	) .
	4
	2. Вычисляем углы поворота и прогибы в сечениях балки и строим эпюры θ и v.
z (м)		0		1		2		3				4			5		6		7				8		9	10
θ		0,0093	0,0096		0,0100			0,0086			0,0045				-		-		-				-		-	-
(рад)														0,0007		0,0054			0,0080				0,0078		0,0069	0,0068
v (мм)		-19,28	-9,83			0		9,59				16,28		18,22			15,08		8,15				0		-7,29	-14,14

Проверка балки на жёсткость в пролёте: v = 18,22 мм < [ f ] = 6000 мм/300 = 20 мм.

Следовательно, условиям прочности и жёсткости удовлетворяет балка, выполненная из прокатного двутавра №30а.

М=6кНм				q1=24кН/м				F=12кН		q2=12кН/м
											z
	2 м			4 м				2 м		2 м
у			RA=65кН						RB=67кН
	65,00				эп.Qy (кН)
			+					24,00	+
						31,00		-
									43,00
			2,7083 м			1,2917 м
			эп.Мх (кНм)							24,00
6,00									-
				+
							62,00
					82,02
0,00925	0,00964	0,01003			эп.	рад)
			+	0,00450		0,00067	0,00540	0,00800	0,00784	0,00694	0,00681
			0,00858
								-
19,28
					эп.V (мм)					14,14
	9,83
										7,29
-
										-
			9,59		+			8,15
				16,28			15,08
					18,22
					Рис. 1.15

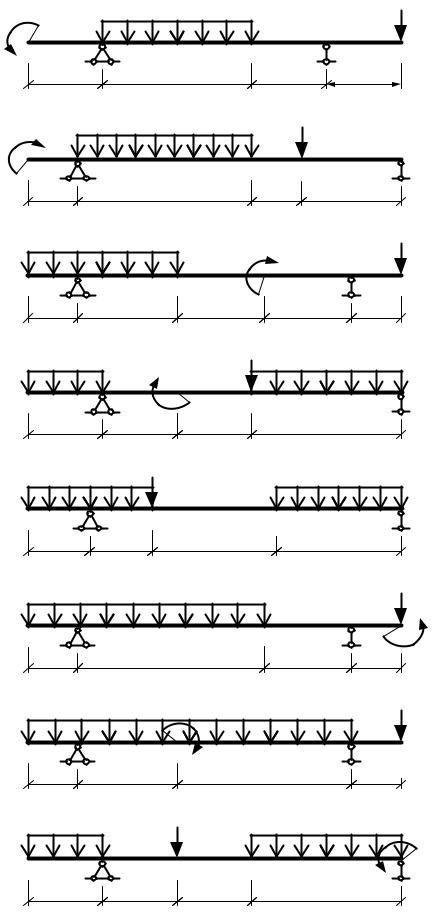
На рис. 1.16 приведены задачи для самостоятельного решения методом начальных параметров. Подобрать сечение стальной балки из прокатного двутавра.

Расчётные характеристики балок: [ σ ] = 160 МПа, [ τ ] = 100 МПа, Е = 2٠105 МПа. Допускаемый прогиб в пролёте балок [ f ] = l / 200, где l – длина пролёта балки.

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

Рис. 1.16

2.Напряженно-деформированное состояние в точке.

2.1Напряженное состояние в точке тела

Значения нормальных и касательных напряжений на произвольных площадках, проходя-

щих через какую-либо точку тела, зависят от положения этих площадок.

Совокупность нормальных и касательных напряжений, действующих на различных пло-

щадках, проходящих через заданную точку, называется напряженным состоянием в этой

точке.

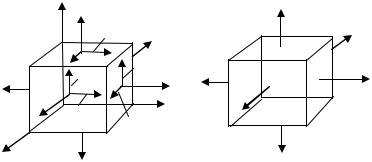
В курсе теории упругости доказано, что в окрестности любой точки можно провести три взаимно перпендикулярные площадки, на которых касательные напряжения будут отсутст-

вовать. Такие площадки называются главными. Нормальные напряжения на главных пло-

щадках принимают экстремальные значения, называются главными напряжениями и обозна-

чаются: σ1, σ2, σ3. Здесь σ1 – наибольшее (в алгебраическом смысле) главное напряжение, σ3 –

наименьшее, а σ2 – промежуточное, т.е. σ1 ≥ σ2 ≥ σ3.

	а)		Y	sY				б)	σ 2	σ 3
					tXY
						sZ
			tZY
						tYX	σ 1			σ 1
sX				tYZ
							sX
		sZ		tXZ					σ 3
						tZX	Х
										s1	¹ 0
Z				sY			s1 ³ s2 ³ s3		σ 2	s2	¹ 0
										s3 ¹ 0
							Рис. 2.1

На рис. 2.1а показаны три взаимно перпендикулярные произвольные площадки, на гранях которых действуют нормальные и касательные напряжения. Нормальные напряжения показаны растягивающими, т.е. положительными. Касательные напряжения (на каждой гра-

ни по два) показаны с двумя индексами: первый индекс указывает параллельно какой оси ко-

ординат действует, а второй – на грани с какой нормалью. В общем случае напряженное со-

стояние в точке описывается тензором напряжений (2.1):

	σX			τXY		τXZ
Tσ =								(2.1)
		τYX		σY		τYZ .
		τ	ZX	τ	ZY	σ
							Z

На рис. 1б показан параллелепипед с бесконечно малыми размерами сторон, грани которого являются главными площадками, так как на них отсутствуют касательные напря-

жения. В зависимости от наличия отличных от нуля главных напряжений на главных пло-

щадках различают три вида напряженных состояний:

	а)	σ 2 ¹ 0					б)
				σ 1 ¹ 0		σ 1			σ 1
σ 1
									s1	¹ 0
				s3 = 0					s2	= 0
		σ 2 ¹ 0							s3	= 0
		Другие возможные комбинации
		При ПНС				При ЛНС
	s1	¹ 0; s3 ¹ 0; s2 = 0;				s3 ¹ 0; s1 = s2		= 0
	s2 ¹ 0; s3 ¹ 0; s1 = 0

Рис. 2.2

1.Если все три главных напряжения отличны от нуля, то имеет место в данной точке

объемное или пространственное напряженное состояние (ОНС) (рис. 2.1б).

2.В том случае, когда два главных напряжения отличны от нуля, а одно равно нулю –

имеет место плоское напряженное состояние (ПНС) (рис.2.2а).

3.Если только одно главное напряжение отлично от нуля, а два других равны нулю,

имеет место одноосное (линейное) напряженное состояние (ЛНС) (рис. 2.2б).

Наиболее простым и наглядным случаем одноосного (линейного) напряженного со-

стояния является центральное растяжение– сжатие стержней.

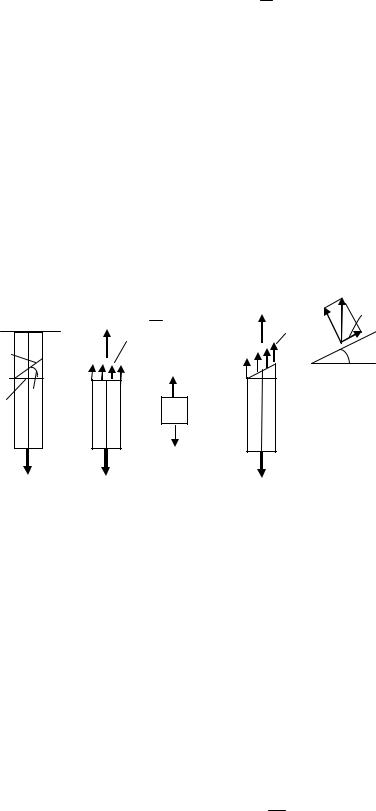
Проведем наклонное сечение n–n 1 под некоторым углом α к поперечному сечению

(рис. 2.3а) и определим действующие в этом сечении напряжения. Площадь наклонного сече-

ния Аα по линии n–n 1 будет больше поперечного сечения А (по линии n–n 2):

Aα = A . cosα

Тогда полное напряжение на наклонной площадке будет равно:

pα =	N	=		F		=	F	×cosα = σ× cosα .	(2.2)
				A
	Aα						A

cosα

Разложив полное напряжение на наклонной площадке по направлениям нормали к площадке и касательной, получим нормальное и касательное напряжения на наклонной площадке

(рис. 2.3г):

σα = pα × cosα = σ× cosα × cosα = σ× cos2α ,				(2.3)
τα	= pα ×sinα = σ× sinα× cosα =	σ	× sin2α .	(2.4)
	2

Из формулы (2.4) следует, что нормальные напряжения σα достигают максимального значе-

ния при α = 0, т.е. в поперечном сечении: σα=0 = σmax = σ1 = F . Поэтому расчет прочности рас-

A

тянутого или сжатого бруса производится по нормальным напряжениям в его поперечных сечениях.

Из формулы (2.5) следует, что касательные напряжения имеют наибольшие и наименьшие значения при α = ±45º:

τ		= τ		= ±	σ	.	(2.5)
	O		max
α=±45				2
			min

Площадки, на которых действуют максимальные и минимальные касательные напряжения

τmax , называются площадками сдвига.

min

а)		б)		в)		г)		pα
							σα
			σ = N		N=F			τα
		N				pα
				A
A α	n1			σ1		n1		α
n
	n2	n	n2		n	n2
α
A
				σ1
F		F				F
				Рис. 2.3

2.2 Обобщенный закон Гука

Установим зависимость относительной линейной деформации от нормальных напряже-

ний в случае объемного напряженного состояния.

Определим относительную продольную деформацию выделенного элемента

(см. рис. 2.1б) в направлении главного напряжения σ1, отдельно рассматривая влияние каж-

дого из главных напряжений и складывая результаты в соответствии с принципом независи-

мости действия сил:

ε1 = ε11 + ε12 + ε13 .

(2.6)

Под действием напряжения σ1 элемент в направлении этого напряжения на основании за-

кона Гука получит относительное удлинение, равное ε11 = σ1 . Аналогично определятся от-

Е

носительные деформации по направлениям двух других главных напряжений:

ε22	=	σ2	; ε	33	=	σ3	.
		Е				Е