9021

80

Рис. 1

Так как векторы p и M 0 M коллинеарны, то их координаты пропорциональны

x x0		y y0		z z0	.	(1)
m		n
				p

Полученное уравнение называется каноническим уравнением плоскости.

2. Параметрическое уравнение прямой

В уравнении (1) введем обозначение

x x0

y y0

z z0

t,

где t

называется

n

p

m

параметром ( t ), тогда

x x0

t

x x

mt

x x

mt

0

0

m

y y0

t

y y

nt

y y

nt

0

0

n

z z0

t

z z

pt

z z

pt

0

0

p

Отсюда получаем:

x x0

m t

y0

n t

y

(2)

z0

p t

z

Это так называемые параметрические уравнения прямой.

3. Уравнение прямой, проходящей через две заданные точки

Пусть прямая l проходит через две точки M1 (x1 , y1 , z1 ) и M 2 (x2 , y2 , z2 ) . Нетрудно понять, что вектор M1M 2 x2 x1; y2 y1 , z2 z1 можно считать направляющим вектором данной прямой. Отсюда, используя уравнение (1),

получим уравнение прямой, проходящей через две заданные точки.

81

x x1		y y1		z z1		(3)
x2 x1		y2 y1		z	2 z1

4. Уравнение прямой как линии пересечения двух непараллельных

плоскостей имеют вид

A1 x B1 y C1z D1	0	(4)
A2 x B2 y C2 z D2	0

Каждое из уравнений этой системы определяет плоскость.

П2

П1

l

Рис. 2

Угол между прямыми в пространстве.

Пусть заданы две прямые l1 и l2 своими каноническими уравнениями:

x x0

y y0

z z0

,

x x0

y y0

z z0

.

m1

n1

p1

m2

n2

p2

Если

m1

n1

p1

, что

означает коллинеарность направляющих

m2

n2

p2

l

и l

векторов

p

и

p

2

,

то

прямые

2

параллельны и угол между ними

1

1

полагают равным нулю. Параллельные прямые, очевидно, принадлежат одной плоскости.

Под углом между пересекающимися прямыми будем понимать угол

между их направляющими векторами p1	и	p2	, если он острый, и угол
в противном случае. Следовательно

82

						p		p												m m					n n							p p
cos	cos					1				2											1			2				1			2		1	2				(4)
						p1				p2								2				2					2					2	2		2
																	m1			n1			p1							m2			n2		p2
Прямые, не лежащие в одной плоскости, называются скрещивающимися
прямыми. Определим понятие угла																		между скрещивающимися прямыми. Под
углом между двумя прямыми l																		и l			2	будем понимать наименьший из углов
											1
между пересекающимися прямыми																		L			и		L			, им параллельными (см. рис. 1).
																			1					2
																							L
																									2
	p1																																			p2
								l																				L
								1																				1
																																	l2
	p2

p1

Рис. 1

В частности, условие перпендикулярности двух прямых имеет вид

l1 || l2 m1 m2 n1 n2 p1 p2 0.

Задания для самостоятельной работы:

1. Написать уравнения прямой, проходящей через точку A4;3;0

параллельно вектору u 1;1;1.

x3 y2 z 3 x1 y 2 z 1

2. Построить прямые и .

1 2 1 5 2 1

	y 3		y 2		x 4
3. Построить прямые: 1)		; 2)		; 3)		.
	z 3		z x 1		z y

4. Составить канонические уравнения прямых, проходящих через точку

		83
M2;0; 3 параллельно:
			x1 y 2 z 1
1) вектору	a 2; 3;5	прямой				;	3) оси	OX	;
	; 2)
			5 2 1

4)оси OY .

5.Составить канонические уравнения прямых, проходящих через две данные точки:

1)	1; 2;1 и	3;1; 1 ;	2) 3; 1;0 и	1;0; 3 ;
3)	2; 1; 3 и	2; 15 ;	4) 4;4;4 и	4;4; 2

6.Составить параметрические уравнения прямых, проходящих через две данные точки:

1)	3; 1;2 и		2;1;1 ;		2) 1;1; 2 и		3; 1;0 ;
3)	2; 1; 3 и		2; 15 ;		4) 2; 1; 1 и		2;1;1 .
7. Через точки		M 6;6;5		и	M 12;6;1	проведена прямая.
			1		2

Определить точки пересечения этой прямой с координатными плоскостями.

8. Даны вершины треугольника A3;6; 7, B 5;2;3, C4; 7; 2.

Составить параметрические уравнения его медианы, проведенной из

вершины C .

9. Проверить, будут ли данные прямые параллельны:

x 2 y 1 z

x

y 1 z

1)

и

;

3 2 1

1

2 3

x 2t 5

x 2 y z 1

y t 2

2)

и

2 3 4 .

z t 7

x 3 y 2 z

10. Найти острый угол

между прямыми:

и

1

1 2

x2 y3 z 5

.

1 1 2

84
	x 3t 2		x 2t 1
11. Найти тупой угол между прямыми	y 0	и	y 0 .
	z t 3		z t 3

x 2 y 1 z

x

y

z

12. Определить угол между прямыми:

и

.

3

2 1

1 1 1

x 2 y z 1

x3 y1 z 7

13. Даны прямые

2

3 4

и

l

4 2. При каком

значении l они перпендикулярны?

14. Найти расстояние

между параллельными прямыми

x2 y1 z 3

x1 y1 z 1

и

.

1

1

2

2

2 2

§ 3. Прямая и плоскость в пространстве

Пусть плоскость задана уравнением П : Ax By Cz D 0 ,

а

прямая

уравнением l :

x x0

y y0

z z0

.

m

n

p

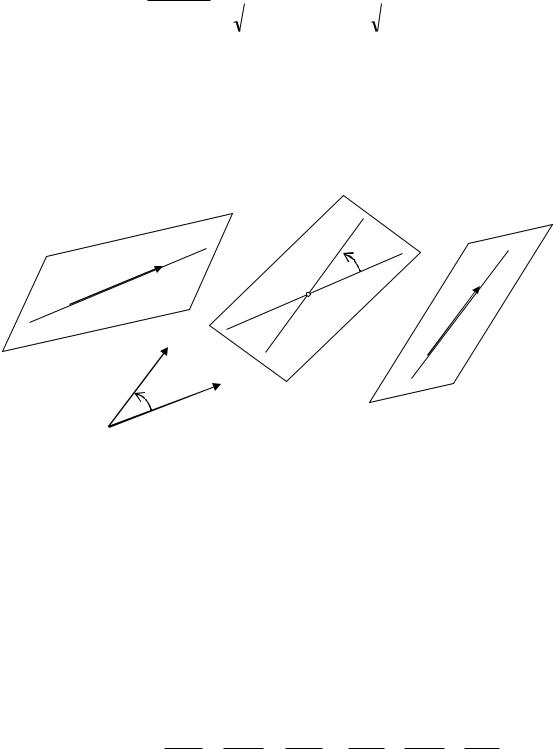
Углом между прямой и плоскостью называется наименьший положительный

угол	между проекцией l прямой l на плоскость П и прямой l (см.
рис.1).

n		l	l	n
	p
		l

l

p

Рис. 1

85

Вычисление угла

можно свести к вычислению угла

между

l

направляющим вектором

p m, n, p прямой

и нормальным к плоскости

p

В случае острого угла 0

имеем

вектором n A, B,C .

2

sin cos

n

p

.

n

p

В случае тупого угла

2

, так как

2

(см. рис. 1),

получим

sin sin( 2 ) cos .

Таким образом, для вычисления угла между прямой и плоскостью получаем формулу

	sin | cos |			| mA nB pC |				.	(1)
			A2	B2 C 2		m2 n2 p2

В частности, условие перпендикулярности и условие параллельности прямой и плоскости имеют вид

l П	A		B		C	;	l || П Am Bn Cp 0.
	m		n
					p
В последнем случае, если дополнительно выполняется равенство
Ax0 By0 Cz0 D 0,		которое означает, что точка M0 ( x0 , y0 , z0 ) прямой l

принадлежит плоскости П, то прямая лежит в этой плоскости.

Таким образом, принадлежность прямой, заданной каноническим уравнением, плоскости, определяется выполнением условий

Am Bn Cp 0

Ax0 By0 Cz0 D 0

Задания для самостоятельной работы:

1. Составить уравнения прямой, проходящей через точку M2; 3; 5 перпендикулярно плоскости 6x 3y 5z 20.

2.Составить уравнение плоскости, проходящей через точку M1; 1; 1

x3 y1z 2

перпендикулярно прямой .

2 3 4

86

	x 3t 2
			4x 3y 6z 50
	3. Доказать, что прямая y 4t 1	параллельна плоскости
			.
	z 4t 5

x1 y 4 z 3

4. Показать,

что прямая

параллельна плоскости

2

1

5

2x y z 0

x1 y1z 3

2 1 3 - лежит в этой плоскости.

,

а прямая

x1 y2 z 3

5. При каком значении m прямая параллельна плоскости

3 m 2

x 3y 6z 70?

6. Написать уравнение плоскости, проходящей через прямую

x 2 y 3z 1

и точку 3; 4; 0 .

1 2 1

7.

Написать уравнение плоскости,

проходящей через параллельные прямые

x 3 y z 1 x 1 y 1 z

и

.

2 1 2

2

1 2

8. Найти точку пересечения:

x 2t 1

3x 2y z 3

1) прямой

y t 2 с плоскостью

;

z 1 t

x y 1 z 1

x 2y 3z 290

2) прямой

с плоскостью

;

2 1

1

9.

Прямая проходит через точки

A 0;0;4 и

B 2;2;0 . Найти точку

пересечения этой прямой с плоскостью x y z 0 и угол между ними.

10.

Найти проекцию точки

M5;2; 1

на плоскость

2x y 3z 230

.

x 3t

M2; 1;3 на прямую

11.

Найти проекцию точки

y 5t 7 .

z 2t 2

12. Найти точку

P , симметричную точке Q1;3; 4 относительно плоскости

3x y 2z 0.

87

Литература

1.Письменный Д.Т. Конспект лекций по высшей математике: Ч. 1.- М.:

Айрис-пресс, 2008. – 288с.

2.Данко П.Е. Высшая математика в упражнениях и задачах: Ч. 1. - М.: ООО

«Издательский дом «Оникс 21 век», ООО «Издательство «Мир и образование», 2003. – 304с.

3.Минорский В.П. Сборник задач по высшей математике. – М. Изд. ф-мат.

лит-ры: 2004. – 336 с.

4.Лунгу К.Н., Письменный Д.Т., Федин С.Н., Шевченко Ю.А. Сборник задач по высшей математике. 1 курс.- 3-е изд., испр. и доп.-М.:Айрис – пресс, 2003.- 576с.

5.Шипачёв В.С. Задачник по высшей математике. М.: Высш. Шк., 2003.-

304с.

88

Содержание

Элементы линейной алгебры

§1. Матрицы и определители…………………………………………….. 3

§2. Системы линейных уравнений. Метод Крамера

решения систем линейных уравнений…………………………………….		6
Элементы векторной алгебры
§ 1. Векторы и линейные операции над ними..…………………………..		9
§ 2. Проекция вектора на ось ………………………………………………		14
§ 3. Координаты вектора и их свойства ……………………………………		18
§ 4. Деление отрезка в заданном отношении …………………………….		24
§ 5. Скалярное произведение векторов…………………………….…….		25
Элементы аналитической геометрии на плоскости
§ 1. Прямая на плоскости…………………………………………..........		29
§ 2.	Линии второго порядка на плоскости…………………………….	47
Элементы аналитической геометрии в пространстве…………………		72
§ 1.	Плоскость в пространстве………………………………………….	72
§ 2.	Прямая в пространстве…………………………………………….	80
§ 3.	Прямая и плоскость в пространстве………………………………..	85
Литература……………………………………………………………......		89

89