10303

U1(x, y) −U0 (x, y) = ∫ P(x, y)dx + Q(x, y)dy = const,

M0M1

аэто говорит о том, что функции U1(x, y) и U0(x, y) отличаются друг от

друга на постоянную величину (также как любые две первообразные для одной и той же функции).

Для вычисления значений функции U0(x, y) можно опять воспользо-

ваться независимостью криволинейного интеграла от пути интегрирования. Пусть точка M(x, y) лежит в области D. Предположим, что ломаная M 0 M 1M (для которойM 0 M 1 параллельна оси OX , аM 1M параллельна оси OY ) целиком лежит в области D. В этом случае точка M1 имеет координаты ( x, y0 ) . При этом вдоль отрезка M 0 M 1 нет изменения переменной y и потому dy = 0 , а вдоль отрезка M1M нет изменения переменной x и потому dx = 0. В таком случае будем иметь

U0 (x, y) = ∫ P(x, y)dx + Q(x, y)dy = ∫ P(x, y)dx + Q(x, y)dy+

	M0M1M	M0M1
	x	y
+ ∫ P(x, y)dx + Q(x, y)dy = ∫ P(x, y0 )dx + ∫Q(x, y)dy.
M1M	x0	y0

И, следовательно, искомая потенциальная функция может вычисляться по формуле

x	y
U0 (x, y) = ∫P(x, y0 )dx + ∫Q(x, y)dy .		(56.7)
x0	y0

Если ломаная М0М1М не лежит целиком в областиD, то можно построить ступенчатую ломаную, звенья которой будут параллельны осям координат и которая целиком лежит в областиD. Тогда значение функцииU0(x, y)

будет равно сумме интегралов по соответствующим переменным по каждому звену этой ломаной.

Следствие. Из приведенных выше рассуждений становится понятным, что, если для поля F(x, y) = {P(x, y), Q(x, y)} существует потенциальная функция U(x,y) , то для любых двух точек A(x1,y1) и B(x2,y2) , лежащих в области D выполняется равенство

∫ P(x,y)dx+Q(x,y)dy=U(B)−U(A)=U(x2,y2)−U(x1,y1) . (56.8)

AB

122

Оно означает, что работа по перемещению материального тела из одной точки пространства в другую равна разности значений потенциальной функции в конечной и начальной точках перемещения.

Пусть дано силовое поле

		x				y
F(x, y) = P(x, y) i+ Q(x, y) j =			,				.
		2 + y2				+ y2
				x	2
x

Покажем, что это поле потенциальное, найдем потенциальную функцию и определим работу по перемещению материального объекта из точки

A(2, 1) в точку B(3, 4) .

Находим	P′	(x, y) = −	2xy	и Q′	(x, y) = −	2xy	.
	y		(x2 + y2)2	x		(x2 + y2)2

Так как эти производные совпадают, то данное поле действительно является потенциальным. Для нахождения потенциальной функции воспользуемся формулой (3.7), взяв в качестве точки M0(x0,y0) точку M0(1,1) . Итак,

			x x			y	y
		U0(x,y)= ∫				dx+∫		dy=
			1 x2 +1			1 x2 +y2				.
1	(ln(x2	+1)−ln2)+1	(ln(x2		+ y2)−ln(x2			+1))= 1	(ln(x2	+ y2)−ln2).
2		2						2

Потенциальная функция определяется с точностью до постоянной величины. Поэтому в качестве потенциальной функции данного силового поля

можно взять и функцию U(x, y) = 1 ln(x2 + y2 ). Работу W по перемеще-

2

нию материального объекта из точки A(2, 1) в точку B(3, 4) определяем теперь как разность потенциалов в этих точках т.е.

W =U(B)−U(A)=U(3,4)−U(2,1)= 1ln25−1ln5= 1ln5.

2 2 2

56.2. Случай пространственного силового поля. Для пространственного силового поля

F(x, y, z) = {P(x, y, z), Q(x, y, z), R(x, y, z)}	(56.9)

аналог теоремы, сформулированной в пункте 55.1, звучит следующим образом.

123

Теорема. Если функции P(x, y, z), Q(x, y, z), R(x, y, z)и частные производные Py′(x, y,z),Pz′(x, y,z),Q′x (x, y,z),Qz′(x, y,z),R′x (x, y,z),R′y (x, y,z)

непрерывны в односвязной пространственной области D, то следующие утверждения эквивалентны:

1) Если замкнутый контур L , целиком лежит в области D, то

∫ P(x, y, z)dx + Q(x, y, z)dy + R(x, y, z)dz = 0.

L

2) Для любых двух точек A и B, целиком лежащих в области D, криволинейный интеграл

∫ P ( x, y, z )dx + Q ( x, y, z )dy + R ( x, y, z )dz

	AB
не зависит от кривой, соединяющей точки A и B.
3) Внутри области		D выполняются тождества
P′(x, y,z) ≡ Q′(x, y,z), P′(x, y,z) ≡ R′, Q′(x, y,z) ≡R′(x, y,z).						(56.10)
y	x	z	x	z	y
4) Существует функция U(x, y,z) , называемая потенциальной функ-
цией векторного поля (56.9), для которой
′		′		′	(x,y,z)=R(x,y,z) ,	(56.11)
Ux(x,y,z)=P(x,y,z) , Uy(x,y,z)=Q(x,y,z)				, Uz

или, иными словами, для которой полный дифференциал определяется по формуле

dU = P(x, y, z) dx + Q(x, y, z) dy + R(x, y, z)dz .

(56.12)

Нахождение потенциальной функции по ее полному дифференциалу в пространстве происходит по схеме, аналогичной плоскому случаю. Пусть M0 (x0, y0,z0 ) – некоторая фиксированная точка в области D, а

M (x, y, z) –произвольная точка в области D. Рассмотрим функцию

U (x, y, z) =	∫	P(x,y,z)dx + Q(x,y,z)dy + R(x,y,z)dz .	(56.13)
0

M0M

Для вычисления ее значений можно опять воспользоваться независимостью криволинейного интеграла от пути интегрирования. Соединим точку

M (x, y, z) ломаной M	0	M	1	M	2	M	такой, чтоM	0	M параллельна оси OX ,
									1
M1M2 параллельна оси OY , а M 2 M параллельна оси OZ . При этом лома-
ная не выходит за пределы области. В этом случае точка M1 имеет коор-
динаты (x, y0,z0 ) , а точка				M2имеет координаты (x,y,z0) .
							124

Пусть

U0 (x, y,z) =	∫	P(x,y,z)dx + Q(x,y,z)dy + R(x,y,z)dz =				∫	+	∫	+	∫
M0M1M2M						M0M1		M1M2		M2M
			, ,
				, ,
		, ,
			,	,
			Рис. 56.2
Но, очевидно, что вдоль отрезкаM 0M1				дифференциалы dy = 0 и					dz = 0,
вдоль отрезка		M1M 2	дифференциалы dx = 0 и dz = 0 , а вдоль отрезка
M 2 M дифференциалы			dx = 0 и dy = 0 . И потому
		x	y		z
U0 (x, y, z) = ∫ P(x, y0 , z0 )dx + ∫Q(x, y, z0 )dy + ∫ R(x, y, z)dz .									(56.14)
		x0	y0		z0

В качестве конкретного примера рассмотрим поле силы тяжести. На

тело массы m вблизи поверхности земли, которую будем считать плоской,

действует направленная вертикально вниз сила тяжести F , величина которой равна mg ( g – ускорение свободного падения).

Рис. 56.3

Очевидно, что в данной ситуации

125

P(x, y, z) = 0, Q(x, y, z = 0, R(x, y, z) = −mg

и условия (56.11) выполнены. Отсюда и из формулы (56.14) следует, что работа при перемещении материального тела из точки M0 (x0, y0,z0 ) в точ-

ку M(x, y,z) будет равна

		z
U0(x, y,z) = ∫	R(x, y,z)dz = − ∫	mgdz = −∫mgdz = −mg(z − z0).
M0M	M0M	z0

Эта работа будет положительна, если точка M0выше точки M, и отрицательна в противном случае. Потенциальная функция U(x,y,z) принимает вид U(x, y,z) = −mgz+C.Принимая значение этой функции на поверхности земли (z = 0) равным 0, получаем, что потенциалом поля силы тяже-

сти является функция

U(x,y,z)=−mgz.

126

Раздел 11. Ряды

Лекция 57. Ряды

В данном разделе мы познакомимся с математическим обоснованием тех вычислительных процедур, которые реализуются (но которые мы даже не замечаем) при использовании в расчетах значений алгебраических, тригонометрических, и более сложной природы функций. Если до появления компьютеров приходилось обращаться к соответствующим таблицам (не задумываясь о том, как они составлены), то теперь вычисление их значений доверяется компьютерам. Но любой компьютер может выполнять лишь четыре арифметических и несколько простейших логических операций (правда, с очень большой скоростью). Теория рядов раскрывает и обосновывает возможность вычисления значения любой функции с заданной точностью путем выполнения указанных простейших операций.

57.1. Числовые ряды. Основные определения. Пусть имеется бес-

конечная числовая последовательность

u 1 , u 2 , u 3 ,..., u n ,... .

Если в этой записи везде вместо запятых поставить знак +, то получившаяся запись

u 1 + u 2 + u 3 + ... + u n + ...

будет называться числовым рядом. Числа u1 ,u 2 ,... называются члена-

ми ряда, а un называется общим членом ряда (предполагается, что n принимает в качестве значения любое целое положительное число). Обычно для записи ряда используется сокращение

						+ u2		+ u3		∞
				u1					+ ... + un + ... = ∑ un .		(57.1)
										n =1
Так, если имеются следующие четыре последовательности
				1,1,1,…,1,….;					1,-1,1,-1,….,(-1	)n,..;
1,	1	,	1	,...,		1	,...	; a , a q , a q 2 , a q 3 , ..., a q n , ... ( a ¹ 0 )			,
2		3				n

то из них можно получить четыре числовых ряда:

∞
1 + 1 + 1 + ... + 1 + ... = ∑1	(57.2)
n =1
∞
1 −1 + 1 −1... + (−1)n + 1 + ... = ∑(−1)n + 1	(57.3)

n =1

127

	1		1		1	1		∞ 1
1 +		+		+		+ ... +		+ ... = ∑n=1		,	(57.4)
	2		3		4		n		n
										∞
a + aq + aq 2			+ aq 3 + ... + aq n + ... = ∑ aq n .								(57.5)

n =0

В связи с чем возникает необходимость в рассмотрении такого бесконечного суммирования? Дело в том, что, как будет показано ниже, значения многих функций при каком-то значении аргумента может быть представлено в виде суммы бесконечного числа слагаемых, причем вычисление каждого слагаемого может быть реализовано посредством четырех арифметических операций: сложения, вычитания, умножения и деления. Чтобы понять, как происходит такое представление, наполним формально введенное понятие числового ряда, математическим содержанием, то есть придадим некоторый смысл процедуре сложения бесконечного числа слагаемых. Естественно при этом отталкиваться от изучения поведения сумм конечного, но все возрастающего числа слагаемых, которые мы будем на-

зывать частичными суммами ряда.

Итак, пусть дан ряд (57.1) и пусть

								n
		S 1	= u 1 ; S2 = u1 + u2 ;		Sn = u1 + u2 + ...+ un		= ∑uk .
								k =1
ВеличинаS		n		(n = 1,2,...) называется n-ой частичной суммой дан-
	n	= ∑ u	k
		k =1
ного ряда. Если последовательность					u 1 , u 2 ,..., u n ,...	определена, то оп-
ределена и последовательность частичных сумм S 1 ,						S 2 ,..., S n ,... . Если
при этом существует конечное число S такое, что lim						S	n	= S ,	то ряд (1)
					n → ∞
называется сходящимся, числоS называется его суммой и этот									факт за-

∞

писывается так ∑ u n = S . Если указанного конечного предела не сущест-

n =1

вует, то ряд (1) называется расходящимся.

Проанализируем приведенные выше примеры (57.2) – (57.5) с точки зрения введенного определения. Рассмотрим ряд (57.2). Для него последо-

вательность частичных сумм S1 , S2 ,..., S n …. выглядит следующим обра-

зом:

S1 = 1 , S2 = 2 ,..., Sn = n ….

Очевидно, что lim S = +∞ и, следовательно, ряд (2) расходящийся.

n→∞ n

Рассмотрим ряд (57.3). Для него последовательность частичных сумм выглядит следующим образом:

S1 = 1 , S2 = 0 , S3 = 1 , S4 = 0 ,..., S2 n −1 = 1, S2 n = 0 .

128

Очевидно, что эта последовательность предела не имеет и потому ряд (57.3) расходящийся.

Рассмотрим ряд (57.5). Его члены представляют геометрическую прогрессию с первым членом u1 = a и знаменателем q . При q=1 ряд расходится. При q ¹ 1 по формуле суммы членов геометрической прогрессии

S n =

a (1 − q n )

=

a

−

a q n

.

1 − q

1 − q

1 − q

При

q

< 1 qn → 0 и, следовательно, ряд (5) сходится и его сумма

S = lim

S

=

a

n

− q .

n → ∞

1

При

q

> 1

q

n → +∞ и, поэтому при

q

> 1ряд (5) расходится.

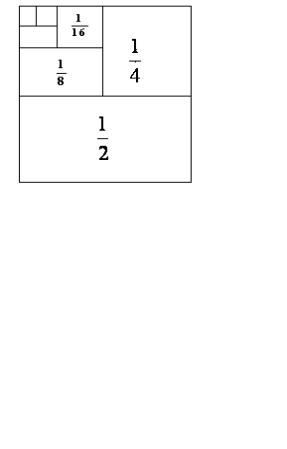
Приa = 1 2 и q = 1 2 сумма S

принимает значение 1 и этот факт

становится наглядно очевидным из Рис. 57.1. На нем представлен квадрат со стороной равной единице длины. Будем представлять первый член суммы как площадь половины этого квадрата, второй – как площадь четверти квадрата и т.д. Интуитивно ясно, что сумма

Sn	=	1	+	1	+	1	+	1	... +	1
										2n
	2		4		8		16

«исчерпает» при n → ∞ всю площадь квадрата, т.е. lim S = 1.

n → ∞ n

Рис. 57.1

Рассмотрим теперь ряд (57.4). Он называется гармоническим рядом. Чтобы понять поведение частичных сумм S1 , S 2 ,..., ,... этого ряда, рассмотрим другой ряд :

1	+	1		+	1		+	1		+	1		+	1		+	1		+	1	+		1	+		1	+		1	+		1	+		1	+		1	+		1	+		1	+	1	+...+	1	+...
		4
2				4			8			8			8			8			16			16			16			16			16			16			16			16			16			32		32
																									129

Члены этого ряда получаются из членов гармонического ряда следующим образом: 1/3 заменяется на меньшее число 1/4, члены с 1/5 до 1/7 заменяются на меньшее число, равное 1/8, члены от 1/9 до 1/15 заменяются на меньшее число 1/16, члены с 1/17 до 1/31 заменяются на меньшее число

1/32 и т.д. Пусть S 1′, S 2′ ,..., S n′ ,...	есть частичные суммы нового ряда. Оче-
видно, что последовательности и	S 1 , S 2 , ..., S n , ... и S	′	, S	′	′	, . . . яв-
		1		2	, . . . , S n
ляются возрастающими. При этом нетрудно видеть, что

S ¢	=	1	,	S¢	=	2	×	1	,…,	S¢n	=	n	×	1
1		2		2				2		2				2
и потому Sn′ → ∞ . Но
	при		n>2		выполняется неравенство Sn′ < Sn . От-

сюда следует, что последовательность Sn также стремится к бесконечно-

сти и, следовательно, гармонический ряд расходится.

При изучении рядов решаются в основном две задачи. Первая задача

состоит в исследовании ряда на сходимость. Вторая задача состоит в

нахождении суммы ряда в случае, если ряд сходится. Вторая задача гораздо сложнее первой, но в некоторых случаях и она поддается решению.

																			∞					1
Пример. Найти сумму ряда ∑																																		,	если он сходится.
																						n ( n + 1)
																			n =1
Так как
																1						=			1				−				1
													n(n + 1)
																									n (n + 1) ,
то для частичной суммы												Snэтого ряда будем иметь:
		1				1				1									1									1								1					1				1			1
S n =				+				+				+ ... +											+												=				-				+			-				+
											4																						1)								2
1		× 2 2 ×					3 3 ×										(n -1)n n(n +																			1									2 3					.
				1				1								1					1							1							1									1
			+				-			+ ... +										-				+							-									=1 -
								4																										(n +1)										n	+1
				3										n -1							n							n
Отсюда следует, что										lim S				n+1		= lim(1 −												1				) = 1				,
										n→∞									n→∞							n −1
и, таким образом,														∞
																			1
														∑															= 1 .
																		n ( n			+			1 )
														n = 1

57.2. Простейшие свойства рядов. Непосредственно из элементарных свойств пределов достаточно просто устанавливаются следующие свойства рядов.

1) Сходимость ряда сохранится, если в нем изменить, убрать или добавить конечное число членов.

130

		∞
	2) Если все члены ряда	∑ uk	умножить на число C , то получится
	∞	k =1
	новый ряд ∑ Сu k . Нетрудно видеть, что, если исходный ряд сходится и
	k =1
	его сумма равна S , то и новый ряд сходится и его сумма равнаCS .
		∞	∞
	Пусть имеются два ряда	∑ uk	и ∑ v k . Суммой (разностью) этих
	∞	k =1	k =1
		± vk ) , элементы которого получены в ре-
	рядов называется ряд ∑ (uk

k =1

зультате сложения (вычитания) соответствующих элементов исходных рядов.

Опять-таки из свойств пределов устанавливается следующий факт.

∞	∞
3) Если ряды ∑ uk	и ∑ v k сходятся и их суммы равны соответст-
k =1	k =1
венно S1 и S2 , то ряд	∞	± vk ) также сходится и его сумма равна
	∑(uk
	k =1

S1 ± S 2 .

Если один из рядов сходится, а другой расходится, то сумма и разность этих рядов будет расходящимся рядом. Если оба ряда расходятся, то никакого общего утверждения о сходимости суммы или разности этих рядов сделать нельзя.

57.3. Признаки сходимости рядов. Рассмотрим ряд признаков, позволяющих устанавливать сходимость или расходимость ряда. Различают необходимые признаки и достаточные признаки сходимости. Отсутствие необходимого признака позволяет сделать вывод о расходимости ряда. Наличие достаточного признака позволяет сделать вывод о сходимости

ряда.

Наиболее легко проверяемый необходимый признак сходимости ряда состоит в следующем.

∞		то lim un = 0 . Т.е. в сходящихся рядах
Если ряд ∑ un сходится,
n =1		n → ∞
общий член обязательно стремиться к нулю.
Действительно, можно записать, что un =Sn −Sn−1. Если ряд (57.1) схо-
дится и S его сумма, то	= lim Sn − lim Sn −1 = S − S = 0 .
lim un
n →∞	n →∞	n→∞
		∞	2n
Пример. Исследовать на сходимость ряд ∑				. Так как
		n =1	3n + 1
		131