ЭММ и ПМ - 2009

41

Выделяют следующие основные элементы симплексного метода:

1)определение какого%либо первоначального допустимого базис% ного решения задачи;

2)правило перехода к нехудшему решению;

3)проверка оптимальности допустимого решения.

Рассмотрим решение задач линейного программирования сим0

плексным методом на следующем примере [1].

Для производства продукции типа П1 и П2 предприятие исполь% зует два вида сырья: С1 и С2. Данные об условиях работы предпри% ятия приведены в табл. 1.

				Таблица 1
		Расход сырья на единицу		Количество
	Сырье	продукции, кг/ед.
				сырья, кг
		П1	П2
	С1	1	3	300
	С2	1	1	150
	Прибыль,	2	3
	тыс. руб./ед. прод.

Требуется составить план производства по критерию “максимум прибыли”.

Экономико9математическая модель задачи

Переменные: х1 — число выпускаемых изделий типа П1; x2 — чис% ло изделий типа П2.

f(x) = 2 х1 + 3 х2 max. Ограничения задачи имеют вид:

х1 +3 х2 300, х1 + х2 150, х1 0; х2 0.

Решение. Приведем задачу к каноническому виду, введя дополни% тельные неотрицательные переменные в систему ограничений задачи:

x1 3x2 x3 300x1 x2 x4 150

x1 0; x2 0; x3 0; x4 0.

42

Матрица, составленная из коэффициентов при переменных x3, x4, имеет определитель, отличный от нуля:

A			1	0	0.
			0	1

Следовательно, переменные x3, x4 можно выбрать в качестве ос% новных переменных на первом шаге, а переменные x1, x2 будут иг% рать роль неосновных.

Шаг 1. Основные переменные x3, x4; неосновные переменные x1, x2.

Выразим основные переменные через неосновные:

x3 300 x1 3x2x4 150 x1 x2 .

Приравнивая неосновные переменные x1, x2 к нулю, получим ба% зисное решение системы уравнений X1 (0;0;300;150). Оно явля% ется допустимым.

Значение целевой функции f(x) = 2 х1 + 3 х2 на этом шаге равно нулю. Это значение можно увеличить путем перевода одной из нео% сновных переменных в основные, что означает переход к новому базисному решению системы, в котором выбранная переменная будет не нулевой, а положительной. Следует выбрать такую пере% менную для перевода из неосновных в основные, чтобы решение не ухудшилось. В случае максимизации целевой функции решение будет улучшаться, если для перевода взять неосновную перемен% ную, входящую в выражение ЦФ с положительным коэффициен% том. В нашем примере такими являются обе неосновные перемен% ные. Увеличение ЦФ будет тем больше, чем больше коэффициент при переводимой переменной. Таким образом, выбираем для пере% вода переменную x2.

Для определения максимально возможного роста переменной x2 составим оценочные отношения, вытекающие из требования нео% трицательности переменных задачи (учтем, что переменная x1 как неосновная равна нулю).

x3 150 3x2 0,

x4 150 x2 0.

43

Решая систему неравенств, получим:

x2 100x2 150.

Сохранение неотрицательности переменных возможно, если мак% симально возможный рост переменной x2 равен 100. При x2=100 пе% ременная x3 обращается в нуль и переходит в основные перемен% ные. Уравнение, в котором достигается наибольшее возможное зна% чение переменной x2, называется разрешающим. В рассматривае% мом примере — это первое уравнение системы.

Шаг 2. Основные переменные x2, x4; неосновные переменные x1, x3.

Выразим основные переменные через неосновные, начиная с раз% решающего уравнения:

x		100	1	x			1	x
	2								3
		3			1	3
						100				1				1		.
x		150 x									x				x
	4			1					3			1	3			3

После преобразований получим:

	x		100		1		x				1		x
		2		3				1		3				3
				2						1
			50									x3 .
	x4					x1
				3						3

Второе базисное решение системы уравнений X2 (0;100;0;50) является допустимым. Составим выражение для целевой функции через неосновные переменные:

					100		1	x1		1	x3
	f(x) = 2 х + 3 х =2 х + 3											=300+ х – x .
							3			3
	1	2	1										1	3

Значение ЦФ на этом шаге равно 300. Значение ЦФ можно уве% личить за счет перевода переменной x1 в основные. Из условия нео% трицательности переменных определим максимально возможный рост переменной x1 (учтем, что переменная x3 как неосновная рав% на нулю):

44

x		100		1		x			0
	2	3					1
			2
x		50			x			0.
	4	3					1

Решая систему неравенств относительно x1, получим:

x1 300

x1 75.

Наибольшее возможное значение x1 равно 75. Второе уравнение является разрешающим, переменная x4 переходит в неосновные.

Шаг 3. Основные переменные x1, x2; неосновные переменные x3, x4. Выразим основные переменные через неосновные, начиная с раз%

решающего уравнения:

x		75	1		x					3	x
	1							3						4
			2							2
				1									1					3		x			1
x		100							75						x				x					x		;
	2		3									2				3	2			4	1	3			3
x		75	1		x					3	x
			2							2
	1							3						4
			1							1
		75										x4 .
x2						x3
			2							2

Базисное решение X3 (75;75;0;0) — допустимое. Получим вы% ражение для ЦФ через неосновные переменные:

f(x) = 300+ х1– x3=300+	75		1	x3		3	x4		– x3=375 –	1	x3		3	x4 .
										2
		2			2							2

Это выражение не содержит положительных коэффициентов при неосновных переменных, поэтому увеличить значение ЦФ, получен% ное на этом шаге, нельзя. Значение f(x) =375 является максимальным.

В некоторых задачах при выборе дополнительных переменных в качестве основных на первом шаге может получиться недопустимое базисное решение. В этом случае рекомендуется изменить базис системы (или перейти к так называемым задачам с искусственным базисом [1]).

45

Ответ

Предприятие получит максимум прибыли в размере 375,0 тыс. руб., если будет выпускать 75 единиц продукции типа П1 и 75 еди% ниц продукции типа П2.

Решение задачи 2

Экономико9математическая модель задачи

Переменные: х1, x2 — число женских и мужских костюмов.

f(x) = 10 х1 + 20 х2 max. Ограничения задачи имеют вид:

x1 x2 150,
2x		1	0,5x	2	240,
		3,5x2		350,
x1
x	2	60,
x1		0.

Замечание. Необходимо также учесть, что число костюмов долж% но быть целым.

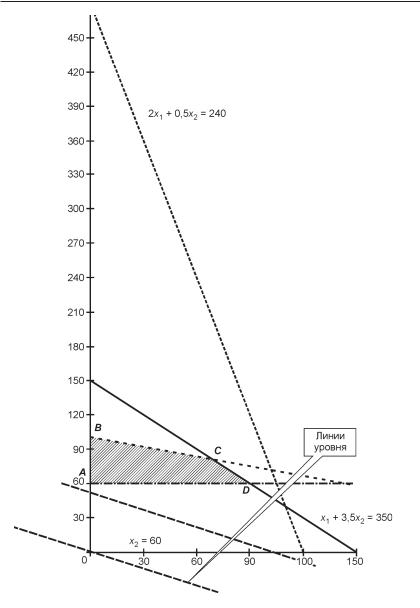
Первое ограничение по труду имеет вид: х1 + х2 150. Найдем пересечение граничной прямой с осями координат. Прямая х1 + х2 = = 150 проходит через точки (150; 0) и (0; 150). Второе ограничение по лавсану имеет вид: 2х1 + 0,5х2 240. Прямая 2х1 + 0,5х2 = 240 про% ходит через точки (120; 0) и (0; 480). Третье ограничение по шерсти имеет вид: х1 + 3,5х2 350. Прямая х1 + 3,5х2 = 350 проходит через точки (350; 0) и (0; 100). Четвертое ограничение по количеству мужских костюмов имеет вид: х2 60. Решением этого неравенства является полуплоскость, лежащая выше прямой х2 = 60.

В результате пересечения построенных четырех полуплоскостей получаем многоугольник ABCD, который и является допустимым множеством нашей задачи. Любая точка этого многоугольника удовлетворяет всем четырем неравенствам, а для любой точки вне этого многоугольника хотя бы одно неравенство системы ограниче%

46

ний будет нарушено. На рис. 1 заштрихована область допустимых решений.

Для определения направления движения к оптимуму построим вектор%градиент С, координаты которого являются частными про% изводными целевой функции, то есть

	f		f
		c ,			c2	(10; 20).
	x		x
		1		2
	1

Чтобы построить такой вектор, нужно соединить точку (10; 20) с началом координат. Для удобства можно строить вектор, пропорци% ональный вектору С. Так, на рис. 1 изображен вектор (30; 60).

Затем построим линию уровня 10x1+20x2=a. Меняя значение a, получим семейство параллельных прямых, каждая из которых яв% ляется линией уровня целевой функции:

10x1+20x2=0 (x1= 30, x2= –15; x1= –30, x2=15),

10x1+20x2=1200 (x1= 0, x2=60; x1= 120, x2=0).

Движение линии уровня будем осуществлять в направлении гра% диента до ее выхода из области допустимых решений. В угловой точке C достигается максимум целевой функции. Для нахождения координат этой точки достаточно решить систему из двух уравне% ний прямых, дающих в пересечении точку максимума:

x1 3,5x2 350

x1 x2 150.

Решая систему, получаем x* 70,	x*	80,
1	2

max f (x) f (x* ) 10 x* 20 x* 10 70 20 80 2300.

12

Ответ

Для получения максимальной прибыли (2300 руб.) необходимо выпустить семьдесят женских (x1* 70) и восемьдесят мужских (x2* 80) костюмов.

47

Рис. 1. Область допустимых решений задачи

48

Решение задачи 3

а) Оценка параметров модели

Линейная модель зависимости объемов платежей Y от сроков (времени) t имеет вид:

Y (t) a0 a1t.

Оценку параметров a0, a1 линейной модели регрессии Y от t прове% дем с помощью надстройки EXCEL Анализ данных. Результат рег% рессионного анализа содержится в нижеприведенных таблицах 2 и 3.

					Таблица 2
Переменная			Коэффициенты	Стандартная	t-статистика
				ошибка
Y-пересечение		a0	38,227	1,955	19,554
t		a1	1,811	0,266	6,818

Во втором столбце табл. 3 содержатся коэффициенты уравнения регрессии a0, a1. Кривая роста зависимости объемов платежей от сроков (времени) имеет вид:

Y (t) 38,23 1,81t.

		Таблица 3
Наблюдение	Предсказанное Y	Остатки
1	40,038	4,962
2	41,850	–1,850
3	43,661	–0,661
4	45,472	2,528
5	47,283	–5,283
6	49,094	–2,094
7	50,906	0,094
8	52,717	2,283
9	54,528	–4,528
10	56,339	0,661
11	58,150	1,850
12	59,962	2,038

49

б) Оценка качества построенной модели

2.1) Оценка адекватности

Для оценки адекватности построенныхˆмоделей исследуются
свойства остаточной компоненты et			yt Yy (табл. 4).
						Таблица 4
	t	Точки		2		2
№		поворота		t		( t t 1)
1	4,962			24,617
2	–1,850	1		3,421		46,392
3	–0,661			0,437		1,413
4	2,528	1		6,391		10,169
5	–5,283	1		27,912		61,015
6	–2,094			4,387		10,169
7	0,094			0,009		4,791
8	2,283	1		5,213		4,791
9	–4,528	1		20,503		46,392
10	0,661			0,437		26,924
11	1,850			3,421		1,413
12	2,038			4,155		0,036
Сумма	0	5		100,902		213,504

При проверке независимости (отсутствие автокорреляции) опре% деляется отсутствие в ряду остатков систематической составляющей, например, с помощью d%критерия Дарбина–Уотсона по формуле:

	n
d	[ t t ]2		213,504	2,12,
	t 2
	n
		100,902
	2t
	t 1

d 4 d 4 2,12 1,88.

Поскольку d попало в интервал от d2 до 2, то по данному крите% рию можно сделать вывод о выполнении свойства независимости.

Это означает, что в ряду динамики не имеется автокорреляции, следовательно, модель по этому критерию адекватна.

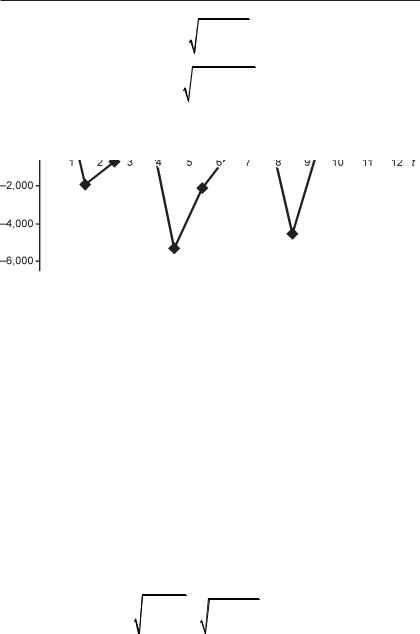
Проверку случайности уровней ряда остатков проведем на ос% нове критерия поворотных точек [1, 2]. Количество поворотных точек (p) равно 5 (рис. 2).

50

				2			16n 29
	p				(n 2)	1,96
				3			90
		2					16 12 29					4,029 4.
			(12 2) 1,96
		3					90

Неравенство выполняется (5 > 4). Следовательно, свойство слу% чайности выполняется. Модель по этому критерию адекватна.

Рис. 2. График остатков

Соответствие ряда остатков нормальному закону распределе0 ния определим при помощи RS%критерия:

RS = [ max – min]/S ;

где max – максимальный уровень ряда остатков, max = 4,962,min – минимальный уровень ряда остатков, min = –5,283, S — среднеквадратическое отклонение,

	S	(t )2		100,902	3,029;
		n 1		11