Мат_модели

составить двойственную.

Решение. Заметим сразу, что x1 ≥1 будем считать нетривиальным ограничением, поэтому задачу можно переписать в виде

z = 4x1 −5x2 +8x3 −10x4 + x5 +14 → min
x	−2x	2	+7x		− x		5	≤ 37,
1				3
−4x1 −7x2 +4x4 −9x5 ≥ −28,
2x +6x			3	−4x	4	+ x = 48,
	1							5
x	≥1,
1
	≥ 0, x3 ≤ 0, x4 ≥ 0.
x2

Выпишем расширенную матрицу полученной задачи

	1 −2 7				0	−1		≤		37
			−7	0	4	−9		≥
	−4									−28
~		2	0	6	−4 1			=		48
A =		1	0	0	0	0		≥		1
		~	≥	≤	≥	~
			−5	8	−10	1				14
	4
											→min

Составляем расширенную матрицу двойственной задачи согласно общим правилам и получаем

	1		−4	2	1		=		4
			−7	0	0		≤		−5
	−2
~		7	0	6	0		≥		8
											.
A′ =		0	4	−4	0		≤		−10
		−1	−9	1	0		=		1
		≤	≥	~	≥
		37	−28	48	1				14
										→max

Двойственная задача имеет вид

T = 37 y1 −28y2 +48y3 + y4 +14 → max

y

−4 y

2

+

2 y

3

+ y

4

=

4,

1

−2 y −7 y

2

≤ −5, 7 y

+6 y

3

≥8,

1

1

4 y2

−4 y3 ≤ −10,

− y

−9 y

2

− y

3

=1,

1

≤ 0, y2 ≥ 0, y4 ≥ 0.

y1

30

Основная связь между двойственными задачами изложена в следующих утверждениях.

Теорема 1 (основное неравенство для двойственных задач). Для всех допустимых решений X ,Y пары двойственных задач имеет место неравенство z(X )≤T (Y ).

Теорема 2 (первая теорема двойственности). Если исходная задача имеет оптимальное решение, то и двойственная ей имеет оптимальное решение. При этом оптимальные значения обеих целевых функций равны, то есть zmax =Tmin .

Чтобы решить задачу линейного программирования, иногда проще решить двойственную задачу, а затем найти решение исходной задачи.

Задачи для самостоятельного решения

Для задач линейного программирования построить двойственные задачи

z = 2x1 −7x3 + 6x4 − 40 → max
x	−3x	+ 4x			= 7,
1	2		3
32. −3x1 −8x2 + 2x4 ≤ 97,
17x1 +3x2 −5x4 ≤15,
x	≥1,
1
	≤ 0, x3 ≤ 0.
x2
z = −4x1 −3x3 +12x4 − x5 −7 → max
−5x +3x +				8x ≥ 5,
	1		2		5
34. 2x1 −6x2 + 7x3 − 4x5 ≤ 70,
3x1 + 2x2 − 4x3 + 6x4 ≥12,
x	≤ 2, x		≥ 7,
2		4
	≥ 0, x3 ≥ 0.
x1

z = −x1 +3x2 +12x3 − x4 +5 → min
−		7x +		2x	−6x	≥ −25,
			1	2	4
33. 4x1 −7x3 +13x4 −8x5 =16,
	−	7x +		4x	+3x	− 46x	≥15,
			1	3	4	5
x			≥1,
	5
		≤ 0, x2 ≤ 0, x4 ≥ 0.
x1
z = 23x1 + 4x2 −7x3 + 4x5 − 28 → min
4x			−3x +		14x ≥ 34,
		1		3	5
35. − x1 − x2 − x3 +18x5 ≤ 5,
x			≥ 3,
	4				0, x ≤ 0.
x		≥ 0, x ≥
	1			2	5

31

§2. Решение двойственных задач с помощью теоремы равновесия.

Сформулируем теперь теорему равновесия (вторую теорему двойственности), которая позволяет не только установить связь между оптимальными значениями целевых функций, но и между точками, в которых

эти значения достигаются.
Теорема	3	(теорема			равновесия). Оптимальные						решения
X = (x1 , x2 ,K, xn )	и	Y = (y1 , y2 ,K, ym ) пары								двойственных задач	связаны
между собой равенствами
				m
			∑aik		yi			−ck		= 0, k =1,K, n,
									xk
		i=1
				n				−bi
			∑aik xk						yi = 0, i =1,K, m.
		k =1
Пример 2. Решить задачу
		z = 22x1 +91x2 −37x3 +19 → min
		−10x1 +7x2 +3x3 ≥1,
		8x1 +2x2 −10x3 ≥ 22,
		x		≥ 0, x		2	≥ 0, x ≥ 0.
		1							3

с помощью теоремы равновесия.

Решение. Составим сначала задачу, двойственную данной. Выпишем расширенную матрицу

	−10		7	3		≥		1
~		8	2	−10		≥		22
A =
		≥	≥	≥
		22	91	−37				19
									→min

и построим расширенную матрицу двойственной задачи

32

			−10		8		≤		22
				7	2		≤		91
~	′										.
A		=		3	−10		≤		−37
				≥	≥
				1	22				19
										→max

Двойственная задача имеет вид

T = y1 +22 y2 +19 → max
−10 y +				8y			2	≤ 22,
			1
						≤ 91,
7 y1 +2 y2
3y			−10 y		2	≤ −37,
	1
y		≥ 0, y		2	≥ 0.
	1

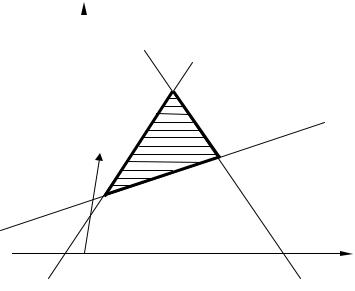
Решим ее графическим способом. Строим на плоскости (y1, y2 ) прямые

l1 : −10 y1 +8y2 = 22 , l2 : 7 y1 +2 y2	= 91,		l3 : 3y1 −10 y2 = −37 и убеждаемся, что не-
тривиальные ограничения определяют треугольник ABC , угловые точки
которого находим из систем уравнений
A = l1 ∩l2	−10 y1 +8y2					= 22,		A(9,14).
	:		+2 y2		=	91,
	7 y1
B = l2 ∩l3	7 y		+2 y		=	91,		B(11,7).
	:	1		2
	3y1 −10 y2 = −37,
	−10 y1 +8y2 =						22,		C(1,4).
C = l1 ∩l3 :			−10 y2 = −37,
	3y1
y2

l2

A

	n	B
l3	C
		y1
l1	O

33

Вектор нормали n имеет координаты n = (1,22). Поэтому, очевидно, мак-

симальное значение функции T (Y ) достигается в точке A(9,14) и

Y = (9,14), Tmax =T (9,14)= 9 +22 14 +19 = 336 .

Запишем теперь теорему равновесия для данной пары двойственных задач

	(−10 y1	+8y2	−22) x1	= 0,
(7 y +2 y −91) x =				0,
	1	2	2
(3y1 −10 y2 +37) x3 = 0,
(−10x1		+7x2	+3x3 −1) y1 = 0,
(8x1 +2x2 −10x3 −22) y2 = 0.

С учетом того, что Y = (9,14) (то есть y1 ≠ 0, y2 ≠ 0 ) и A = l1 ∩l2 , A l3 (то есть

−10 y1 +8y2 −22 = 0, 7 y1 +2 y2 −91 = 0 , 3y1 −10 y2 +37 ≠ 0 , в чем можно убедить-

ся непосредственной подстановкой), выполнение первых двух уравнений очевидно, третье сводится к условию x3 = 0 и система сводится к виду

= 0,

= 0,

x3

или

x3

решениями которой

−10x1 +7x2 +3x3 −1 = 0,

−10x1 + 7x2 −1 = 0,

= 0.

− 22

= 0,

8x1

+2x2

−10x3 −22

8x1

+ 2x2

является

точка

X * = (2,3,0).

Заметим,

что

z(X * )= 22 2 +91 3 −37 0 +19 = 336 =T (Y * ),

как и должно быть по первой тео-

реме двойственности.

Задачи для самостоятельного решения

Для следующих задач линейного программирования а) построить задачу, двойственную данной; б) решить двойственную задачу графическим методом;

в) найти решение исходной задачи с помощью теоремы равновесия.

36. z = x1 +154x2 −21x3 → min при x ≥ 0 и	−13x1 +8x2 +5x3 ≥ −18,
		7x1 + 6x2 −13x3 ≥ 20.

34

сбаз

37.	z = x1 + 4x2 − 2x3	− 2x1 + x2 + x3 ≥ −4,
		→ min при x ≥ 0 и
		7x1 + 4x2 −11x3 ≥ 29.
38.	z = 20x1 +108x2 −51x3 → min при x ≥ 0 и		−8x1 +3x2 +5x3 ≥ −13,
			− x1 + x2 − 2x3 ≥ 3.
39.	z = −10x1 + 44x2	+ x3 → min при x ≥ 0 и	−5x1 + x2 + 4x3 ≥ −4,
			5x1 + 6x2 −11x3 ≥11.
40.	z = 3x1 +58x2 −13x3 → min при x ≥ 0 и −9x1 + 2x2 + 7x3 ≥ −25,
		6x1 + 4x2 −10x3 ≥ 22.
41.	z = −10x1 +56x2	−3x3 → min при x ≥ 0 и	−12x1 + 7x2 +5x3 ≥ −22,
				x1 +3x2 − 4x3 ≥ 9.

§3. Решение двойственных задач с помощью симплекс-метода

Решение пары двойственных задач может быть основано на следующем правиле.

Теорема 4. Если для одной из задач оптимальное решение найдено симплекс-методом, то в исходной задаче можно выделить квадратную матрицу P, образованную столбцами, соответствующими базисным переменным оптимального решения. Тогда оптимальное решение двойственной задачи находится по формуле

Y * = cбаз P−1 ,

где – вектор-строка, образованная коэффициентами при базисных

переменных заключительной симплекс-таблицы в целевой функции исходной задачи.

Пример 3. Для задачи

z = 23x1 + 40x2 + 60x3 + 2x4 − x5 −18 → max4x1 +10x2 +11x3 + x4 + x5 = 57,

2x −6x2 − x3 + x4 − x5 = 9,

	≥ 0, j =1,..,5.
x j

35

построить двойственную, решить исходную задачу симплекс-методом и найти оптимальное решение двойственной задачи.

Решение. Составим задачу, двойственную к данной. Образуем расширенную матрицу

	4		10	11	1	1		=		57
~		2	−6 −1 1			−1		=		9
A =												,
		≥	≥	≥	≥	≥
	23		40	60	2	−1				−18 →max

и преобразуем ее по общему правилу

	4		2		≥		23
			−6		≥		40
	10
~			−1		≥		60
	11								.
A′ =		1	1		≥		2
		1	−1		≥		−1
		~	~
	57		9				−18 →min

Двойственная задача имеет вид

	4 y + 2 y					≥ 23,
		1			2
	10 y1 −6 y2 ≥ 40,
T = 57 y1 +9 y2	−18 → min, при условиях 11y1 − y2					≥ 60,
	y	+ y	2	≥ 2,
	1
		− y2		≥ −1.
	y1

Решим исходную задачу симплекс-методом. В задаче не выделен допустимый базис, поэтому для его нахождения можно использовать метод искусственного базиса или выделить его непосредственно из нетривиальных ограничений: сложим уравнения, а затем вычтем из первого второе. Получим систему

6x

+ 4x

2

+10x

3

+ 2x

4

= 66,

3x

+ 2x

2

+5x

3

+ x

4

= 33,

1

1

2x1

+16x2 +12x3 + 2x5

= 48,

x1

+8x2

+ 6x3 + x5

= 24.

с выделенным базисом x4 , x5 . Выражаем базисные переменные x4 , x5

x4 = 33 −3x1 −2x2 −5x3 , x5 = 24 − x1 −8x2 −6x3

36

и подставляем полученные выражения в формулу для z . Получим задачу

z =18x1 + 44x2 +56x3 + 24 → max
	+ 2x2 +5x3 + x4 = 33,		.	( )
3x1
x1 +8x2		+ 6x3 + x5 = 24,
	≥ 0,	j =1,..,5
x j

Перепишем целевую функцию в виде

z−18x1 −44x2 −56x3 = 24

иимеем симплекс-таблицу

базис	bi	x1	x2	x3	x4	x5
x4	33	3	2	5	1	0
x5	24	1	8	6	0	1
z	24	−18	− 44	−56	0	0

	Вводим в базис переменную			33		24			24
		x3	. Находим min		,			=		= 4	и выводим
				5		6			6

из базиса переменную x5 . Делим соответствующую строку на 6 и получаем

базис	bi	x1	x2	x3	x4	x5
x4	33	3	2	5	1	0
x5	4	1/ 6 4 / 3		1	0	1/ 6
z	24	−18	− 44	−56	0	0

базис	bi	x1	x2	x3	x4	x5
x4	13	13 / 6 −14 / 3 0			1	−5 / 6
x3	4	1/ 6	4 / 3	1	0	1/ 6
z	248	− 26 / 3	92 / 3	0	0	28 / 3

В строке оценок осталась единственная отрицательная оценка, а так как

	13		4			= 6 , то выводим из базиса переменную x1	и вводим x4 . Ум-
min		,
			1/ 6
13 / 6

ножаем первую строку на 6 /13 , получаем симплекс-таблицу

базис	bi	x1	x2	x3	x4	x5
x4	6	1	− 28 /13 0		6 /13 −5 /13
x3	4	1/ 6	4 / 3	1	0	1/ 6
z	248	− 26 / 3	92 / 3	0	0	28 / 3

и делаем шаг симплекс-метода:

37

базис	bi	x1	x2	x3	x4	x5
x1	6	1	− 28 /13	0	6 /13	−5 /13
x3	3	0	22 / 3	1	−1/13	3 /13
z	300	0	12	0	4	6

Так как в строке оценок нет отрицательных элементов, то полученная симплекс-таблица – заключительная, оптимальное решение X * = (6,0,3,0,0)

и zmax = z( X * ) = 300 .

Базисными переменными оптимального решения являются x1, x3 ,

поэтому из исходной задачи находим	4		11	, а из условия задачи
	P =
		2
			−1

cбаз = (23,60) , поэтому оптимальным решением двойственной задачи будет

	*	4		11 −1	11				1
Y		= (23,60)			=			,			,
			2			2			2
				−1

причем Tmin = T (Y * ) = 57 112 +9 12 −18 = 300 = zmax .

Если в задаче линейного программирования выделен допустимый базис и базисные переменные исключены из целевой функции, то оптимальным решением двойственной задачи являются элементы строки оценок последней симплекс-таблицы при базисных переменных исходной симплекс-таблицы. Например, для задачи ( ) двойственной задачей будет

T = 33y1 + 24 y2 + 24 → min

3y1 + y2 ≥18,2 y1 +8y2 ≥ 44,5y1 + 6 y2 ≥ 56,

y1 ≥ 0,

y ≥ 0.2

и общая формула теоремы 4 дает

Y * = (18,56) 3 5 −1 = (4,6), T (Y * )= 33 4 + 24 6 + 24 = 300 .

1 6

38

С другой стороны, оптимальное решение Y * = (4,6) легко находится из

строки оценок последней симплекс-таблицы как коэффициенты при базисных переменных x4 , x5 исходной.

Задачи для самостоятельного решения

Для следующих задач линейного программирования а) построить задачу, двойственную данной;

б) решить исходную задачу симплекс-методом и найти решение двойственной задачи.

42.	z = x1	+3x2 +3x3 + x4		+ x5	+ 7 → max при x ≥ 0 и 4x1 +3x2 + x3 − 2x5		= 5,
						2x1 + 2x2 + x4 + 2x5 = 2.
43.	z = 2x1 + x2 + x3		− x4 − x5 +8 → max при x ≥ 0 и 2x1 −3x2 + x3 + x4 = 9,
						3x1 + 2x2 + x3 + x5 = 7.
44.	z = x1	− x2 + 2x3	+ 2x4	− x5	+13 → max при x ≥ 0 и 3x1 − x2 + 4x3 + x4		= 3,
						2x1 + x2 + 2x3 + x5	= 7.
45.	z = x1	− 2x2 + x3	+ 2x4	+ 4x5 + 23 → max при x ≥ 0 и x1 + 4x2 + x4 − 2x5 = 4,
						−5x2 + x3 + 6x4 +5x5 = 5.
46.	z = 52x1 + 72x2 + 61x3			+ x4	+ x5	+8 → max при x ≥ 0 и 2x1 + 6x2 + x3 + x4 = 22,
						3x1 + 2x2 +5x3 + x5		= 40.
47.	z =12x1 +13x2 + x3 + 7x4 −3x5					+ 2 → max при x ≥ 0 и 16x1 + x2 −7x4	+13x5 = 3,
						− 2x1 + x3 +5x4 + x5		=15.

39