Общий отчёт по МО

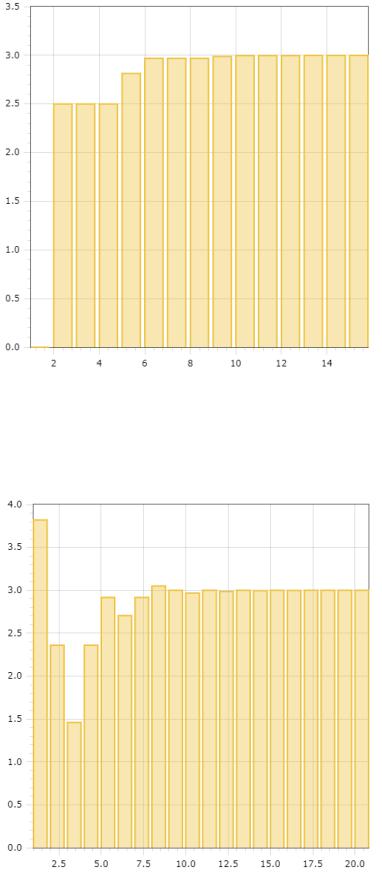
Рисунок 2.14 – Гистограмма поиска минимума для метода дихотомии

(функция 4-7*2.71^(-(x-3)^2))

Рисунок 2.15 – Гистограмма поиска минимума для метода Фибоначчи

(функция 4-7*2.71^(-(x-3)^2))

21

2.6Многомерная оптимизация без ограничений

2.6.1Метод Нелдера-Мида

Пусть ( ( )), i = 1, 2, ..., n+1 - зафиксированные вершины многогранника.

В начале итерации определяются «тяжелая» ( ) и «легкая» ( ) вершины

(вершины с максимальным и минимальным значением функции соответственно)

(( )) = max { (( ))},

=1, +1

(( )) = min { (( ))},

=1, +1

смещенный центр тяжести вершин многогранника ( +2) (смещенный, так как не учитывает тяжелую точку ( ), чтобы максимально от нее отдалиться):

( +2) = 1 ∑ =1+1 ( ) , ≠ ,

иточка отражения ( +3) - проекция тяжелой точки ( ) через центр тяжести

( +2):

( +3) = ( +2) + (( +2) − ( )),

где 0 – коэффициент отражения. По рекомендации авторов метода задаем

=1, но при медленной сходимости к минимуму параметр можно немного увеличить.

Затем, в зависимости от значения функции в точке отражения,

выполняется одна из следующих операций:

1. Растяжение выполняется, если точка отражения «легче» всех вершин

(( +3)) < (( )),

и заключается в вычислении точки растяжения ( +4):

22

( +4) = ( +2) + ( ( +3) − ( +2)),

где 0 – коэффициент растяжения; по рекомендации авторов = 2, но при необходимости можно задавать 2 3.

2. Сжатие выполняется, если точка отражения «легче» только

«тяжелой» вершины

( ( +3)) > ( ( )), ≠ ,

изаключается в вычислении точки растяжения ( +5):

( +5) = ( +2) + ( ( +2) − ( )),

где 0 < < 1 – коэффициент сжатия; по рекомендации авторов = 0.5 ,

но при необходимости можно задавать 0.4 0.6.

3. Редукция выполняется, если точка отражения «тяжелее» всех вершин:

( ( +3)) > ( ( )),

В результате этой операции перевычисляются координаты всех вершин многогранника в соответствии с соотношением:

( )

( )

=

=( ) + 0.5 ( ( ) − ( )),

=( ),

1, 2, … , + 1,

то есть точки стягиваются к «легкой» вершине и стороны многогранника уменьшаются в два раза. Учащение выполнения этой операции часто показывает, что точка минимума находится уже либо внутри многогранника, либо просто рядом с ним (то есть «захват» растяжением для примерного определения местонахождения минимума уже не нужен).

23

Далее после выполнения операций происходит вычисление значений функции в новых точках, сравнение их со значениями функций в новых вершинах и выбор новых вершин, которые предположительно находятся ближе к минимуму функции. Критерий останова состоит в проверке условия

+1

√ +1 1 ∑( ( ( )) − ( ( +2)))^2 <

=1

или более мягкого альтернативного условия

	1	+1
		∑( ( ( )) − ( ( +2))) ^2 <
	+ 1
		=1

2.6.2Метод наискорейшего спуска

Вотличие от предыдущего метода, требующего задавать величину шага спуска вручную перед началом работы, данный алгоритм использует автоматический выбор шага на каждой итерации.

Исходные данные: точка начального приближения X 0 ; общее количество итераций N ; точность решения задачи .

Итерационная формула:

[ + 1] = [ ] − ( [ ]).

Шаг k t определяется из условия:

( ) = min ( ) = min ( [ ] − ( [ ])).

>0 >0

При минимизации квадратичной функции для отыскания можно

использовать необходимое условие экстремума:

24

Условие останова: |	f( [ ])	̅̅̅̅	или выполнено N итераций.
		| < , = ,
		′( ) = 0

Из условия выбора шага в методе наискорейшего спуска следует, что

направления спуска на соседних итерациях ортогональны. Для доказательства достаточно в уравнении (1) записать (t) как производную

сложной функции многих переменных.

2.6.3 Овражный метод (метод большого овражного шага)

Исходные данные: точка начального приближения X 0 ; t=const -

величина овражного шага; общее количество итераций N , точность решения задачи .

Суть метода заключается в следующем: в окрестности точки очередного приближения X k выбирают точку X k . Спуском из точек X k и ̃ k находят две точки на «дне оврага» X и X , с использованием которых «дно оврага» аппроксимируют прямой линией. Вдоль полученной прямой делают шаг в направлении убывания функции и получают точку следующего приближения:

[ + 1] = ′ − ( ′′ − ′) ( ′′)− ( ′),

|| ′′− ′||^2

|| || - обозначение нормы или длины вектора.

Обратите внимание, что если разделить квадрат в знаменателе формулы на два множителя и расписать две отдельные дроби:

[ + 1] = ′ − ( ′′− ′) ( ′′)− ( ′), || ′′− ′|| || ′′− ′||

то можно увидеть, что сохраняется структура формулы методов спуска

(точнее, покоординатного спуска): первая дробь, очевидно, является

25

единичным вектором (так как вектор делится на свою длину), а вторая дробь

– своеобразным приближением производной.

Останов происходит, как правило, по заданному количеству итераций.

Однако на практике при работе с методом большого овражного шага процесс останавливают в том случае, когда несколько раз будет зафиксировано движение с резким увеличением целевой функции.

2.7 Вывод программы для вычисления точек минимума

На рисунках 2.16–2.24 показаны выводы программы для трёх заданных вариантом функций.

Рисунок 2.16 – Вывод программы для функции 4*(x-7)^2+3*(y-1)^2

26

Рисунок 2.17 – Продолжение вывода программы для функции 4*(x- 7)^2+3*(y-1)^2

27

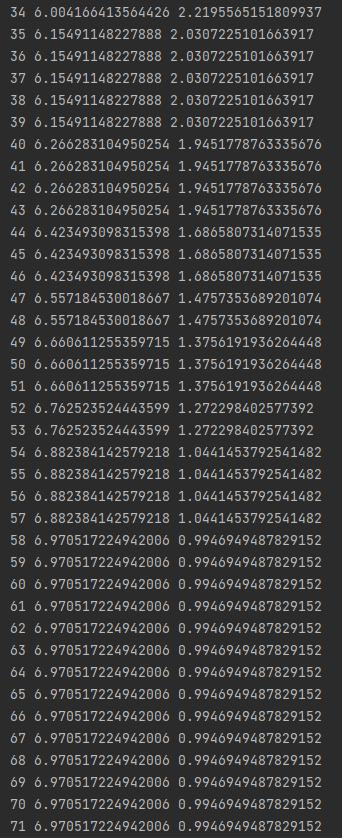
Рисунок 2.18 – Продолжение вывода программы для функции 4*(x- 7)^2+3*(y-1)^2

28

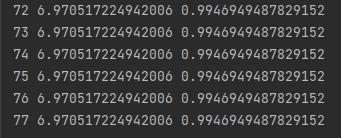
Рисунок 2.19 – Продолжение вывода программы для функции 4*(x- 7)^2+3*(y-1)^2

29

Рисунок 2.20 – Вывод программы для функции (x-4)^2+(y-7)^2+30*(x+y-

6)^2+7.1

30