
3 лаба численные методы
.pdfМинистерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра комплексной информационной безопасности электронно-
вычислительных систем (КИБЭВС)
Интерполяция и аппроксимация Отчет по лабораторной работе №3 по дисциплине «Численные методы»
Студент гр. 711-2
_______ Е. П. Толстолес
_______
Принял:
Ст. преподаватель кафедры КИБЕВС
_______ А. Ю. Якимук
_______
Томск 2022
1 Введение
Необходимо для функции ( ) = cos (6,64 2 + 2,49) вычислить интерполяционный полином и аппроксимирующую функцию.
Порядок действий:
1. Вычислить пары точек ( ; ), где |
̅̅̅̅̅̅̅̅̅̅̅ |
|
= ( ), ( ) - |
|||
= 0.2 , = 0,13, |
||||||
|
|
|
|
|
|
|
индивидуальная функция.
2. Запрограммировать вычисление интерполяционного полинома Лагранжа
2 степени по заданным точкам.
3. По методу наименьших квадратов рассчитать параметры функции (̅ ) =2 + + аппроксимирующей функцию f(x) . Построить график
зависимости f(x) от x, вывести линии полиномиального (2 степени) тренда,
уравнение тренда и коэффициент детерминации R2.
Взять произвольный узел , > 2, промежуточную точку ( , +1), j>3, выбрать точку прогноза ̅> 11, и для всех 3 точек заполнить таблицу:
x |
f(x) |
L(x) |
̅ |
( ) |
2

2 Ход работы
2.1Интерполяционный полином Лагранжа
Вобщем виде интерполяционный многочлен в форме Лагранжа записывается в следующем виде:
|
|
− |
|
|
|
||
( ) = ∑ ( ) |
∏ |
|
|
− |
|||
−0 |
=0, =0 |
|
|
где n – степень полинома;
f( ) значение интерполирующей функции f(x) в точке ;
( ) базисные полиномы (множитель Лагранжа), которые определяются
по формуле: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
− |
|
− |
− |
|
− |
|||||
( ) = ∏ |
|
|
= |
0 |
… |
|
−1 |
. |
|
+1 |
… |
|
|
− |
− |
|
|
− |
− |
||||||||
|
|
|
− |
|
|||||||||
=0, ≠ |
|
|
|
0 |
|
|
−1 |
|
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так, например, интерполяционный многочлен в форме Лагранжа,
проходящий через три заданные точки [x1, f(x1); x2, f(x2); x3, f(x3)] , будет записываться в следующем виде:
|
( − ) ( − |
) |
|
( − ( − |
)) |
|
|||
( ) = ( ) |
|
|
2 |
|
+ ( ) |
0 |
2 |
|
+ ( ) |
|
|
|
|
|
|
|
|||
0 |
(0 |
− 1) (0 |
− 2) |
1 |
(1 − 0) (1 − 2) |
2 |
|||
|
|
|
|||||||
( − 0) ( − 2) (1 − 0) (1 − 2)
2.2 Аппроксимирующая функция по методу наименьших квадратов
3

Для расчета коэффициентов аппроксимирующей функции (̅) = 2 ++ применяется метод наименьших квадратов.
0 1 2|0
Расширенная матрица системы уравнений: [ 1 2 3|1], решив
2 3 4|2
которую получим искомые коэффициенты a, b,c.
= |
∑ |
0 |
= + 1, |
|
= ∑ |
|
, |
|
= ∑ |
2 |
, |
|
= ∑ |
, |
= |
||
0 |
=0 |
|
|
|
1 |
=0 |
|
2 |
=0 |
|
|
0 |
=0 |
|
2 |
||
∑ |
, , = ∑ |
3 |
, = ∑ |
4, = |
∑ |
2 |
|
|
|
|
|
||||||
=0 |
|
3 |
=0 |
|
4 |
=0 |
|
|
2 |
=0 |
|
|
|
|
|
|
|
Коэффициент детерминации ( 2) — это доля дисперсии, зависимой перемен-
ной, объясняемая рассматриваемой моделью. Более точно — это единица ми-
нус доля необъяснённой дисперсии (дисперсии случайной ошибки модели,
или условной по признакам дисперсии зависимой переменной) в дисперсии зависимой переменной. В случае линейной зависимости R2 является квадратом так называемого множественного коэффициента корреляции между зависимой переменной и объясняющими переменными.
Коэффициент корреляции:
= √1 − ∑( − )^2 ∑( − ̅^2)
1 ̅ = ∑
= 2 + +
Результаты работы программы представлены на рисунках 2.1 и 2.2.
4
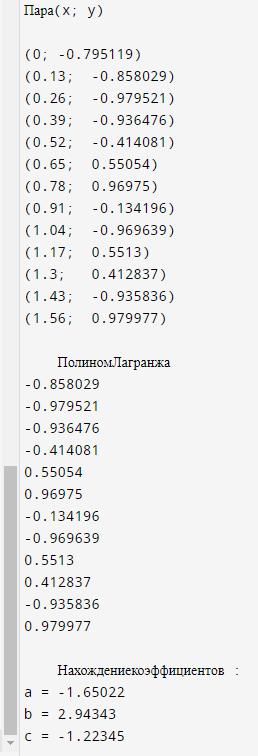
Рисунок 2.1 – Результат работы программы
5

Рисунок 2.2 – Продолжение вывода работы программы
2.3 Результаты вычислений
Результаты вычислений представлены в таблице 2.1.
Таблица 2.1 – Результаты вычислений
|
( ) |
2( ) |
̅ |
(x) |
|||
(5) |
0.403001 |
-510.921 |
-27.7619 |
|
|
|
|
|
|
|
|
(7.5) |
0.539361 |
-1411.4 |
-71.9728 |
|
|
|
|
̅1 (2.4) |
-0.994565 |
-49.203 |
-3.6645 |
|
|
|
|
̅2 (6) |
-0.931371 |
-817.403 |
-42.9709 |
|
|
|
|
6
3Выводы
Врезультате выполнения данной лабораторной работы были получены навыки разработки программ, использующих в своей работе вычисление интерполяционного полином Лагранжа и вычисление аппроксимирующей функции по методу наименьших квадратов.
Отчет написан согласно ОС ТУСУР 2021.
7
Приложение А
(обязательное)
Листинг кода программы
#include <iostream> #include <cmath> #include <math.h> using namespace std;
double func(double x) { return cos(6.64*x*x+2.49); } //функция из задания
double n[14] = { 0,0.13,0.26,0.39,0.52,0.65,0.78,0.91,1.04,1.17,1.30,1.43,1.56,1.69};
struct coord { double y;
};
double a[3][4]; coord tabl[13];
double Lagrange(double x, int i) { return (((x - n[i])*(x - n[i + 1])) / ((n[i - 1]
-
n[i])*(n[i - 1] - n[i + 1])))*tabl[i - 1].y + (((x - n[i - 1])*(x - n[i + 1])) / ((n[i] -
n[i -
8
1])*(n[i] - n[i + 1])))*tabl[i].y + (((x - n[i - 1])*(x - n[i])) / ((n[i + 1] - n[i - 1])*(n[i
+ 1] - n[i])))*tabl[i + 1].y; }
int main() { setlocale(LC_ALL, "Russian");
cout << "\nПара(x; y)\n" << endl; for (int i = 0; i < 13; i++) {
tabl[i].y = func(n[i]);
cout << "("<< n[i] << ";" << "\t" << tabl[i].y << ")" << endl;
}
cout << "\n\tПолиномЛагранжа" << endl; //ПолиномЛагранжа for (int i = 1; i < 13; i++) {
cout << Lagrange(n[i], i) << endl;
}
double d, x[3], x0, tempX1, tempX2, tempX3;
cout << "\n\tНахождениекоэффициентов : " << endl; //НахождениекоэффициентовпометодуГаусса
for (int i = 0; i <= 11; i++) { a[0][0] += pow(n[i], 0); //c a[0][1] += n[i]; //b
9
a[0][2] += pow(n[i], 2); //a a[0][3] += tabl[i].y; //f(x) a[1][0] += n[i];
a[1][1] += pow(n[i], 2); a[1][2] += pow(n[i], 3); a[1][3] += tabl[i].y*n[i]; a[2][0] += pow(n[i], 2); a[2][1] += pow(n[i], 3); a[2][2] += pow(n[i], 4);
a[2][3] += tabl[i].y*pow(n[i], 2);
}
for (int k = 0; k < 3; k++) {
for (int i = k + 1; i < 3; i++) { d = -(a[i][k] / a[k][k]);
for (int j = k; j < 4; j++) { a[i][j] = a[i][j] + a[k][j] * d;
}
}
}
x[2] = a[2][3] / a[2][2];
10
