138

Линии второго порядка Лекция 14 Эллипс. Гипербола. Парабола

§ 28. Эллипс

Эллипсом называется множество всех точек плоскости, сумма расстояний каждой из которых до данных точек иравна длине данного отрезка, где.

Коротко можно записать определение эллипса так:

. (37)

Точки иназываютсяфокусами эллипса, а расстояние между ними - фо­кальным расстоянием.

Если  точка данного эллипса, то отрезки и(а также их длины) называютсяфокальными радиусами точки .

П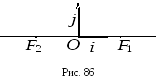усть на плоскости даны две различные точкии. Обозначим черезсе­редину отрезка. Рассмотрим прямоугольную декартову систему координат, где(рис. 86).

Выведем уравнение эллипса с фо­кусамиив системе координат.

Пусть .

Замечание. Так как , то для эллипса всегда, т.е.

.

Пусть . Так какв, то

.

По определению эллипса . Преобразуем это уравнение:

;

;

;

;

;

;

.

Возведем обе части последнего уравнения в квадрат:

;

;

.

Разделим обе части этого уравнения на :

.

Так как для эллипса , то. Положим. Тогда

, где . (38)

Итак, доказано, что если , то координаты точкиудовлетворяют урав­нению (38).

Докажем, что если координаты точки удовлетворяют уравнению (38), то она принадлежит эллипсу.

Пусть , где ,  координаты точки .

Найдем . Выразимиз уравне­ния:

.

Тогда, учитывая, что , получим:

.

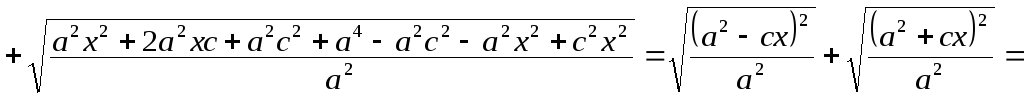
и ии. Из условия (37) следует, что.

Итак, уравнение (38) есть уравнение эллипса. Оно называется каноническим уравнением эллипса.

Если , то, т.е.  уравнение окружности радиуса .

Пользуясь каноническим уравнением эллипса, докажем геометрические свойства эллипса, которые понадобятся для построения изображения эллипса.

Свойства эллипса

1. Из уравнения (38) следует, что ,. Следовательно, все точки эл­липса принадлежат прямоугольнику, центр которого находится в точке, стороны параллельны осямии равны соответственнои(рис. 87).

2. Симметрия относительно начала координат и осей координат.

Пусть и. Из первого тождества следует, что, из второго – что, из третьего – что, а это означает, что эллипссимметричен относительно начала координат, осии осисоответственно. Таким образом, точкаявляетсяцентром симметрии, оси и осями симметрии эллипса .

Прямая, проходящая через фокусы, называется первой (фокальной) осью симметрии, а перпендикулярная к ней ось – второй осью симметрии эллипса.

3. Точки пересечения эллипса с осями симметрии.

Чтобы найти точки пересечения эллипса с осью, надо решить систему их уравнений:

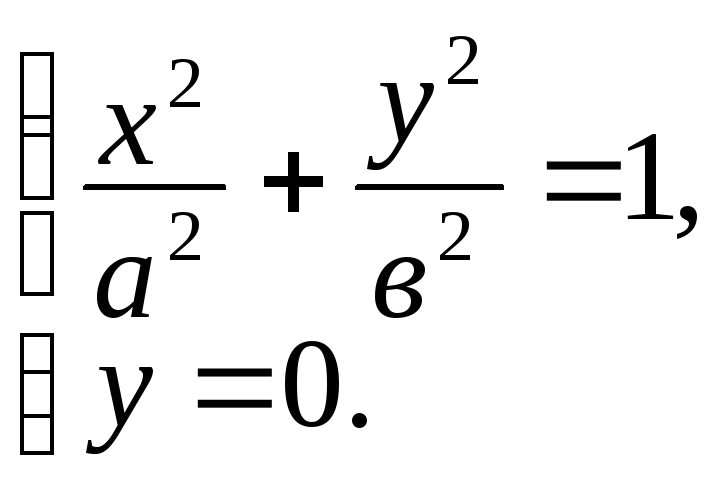
Решая систему, получаем: .

Аналогично находим, что .

Точки пересечения эллипса со своими осями симметрии называются вершинами эллипса. Таким образом, эллипс имеет четыре вершины.

Отрезки иназываются соответственнобольшой и малой «осями» эллипса, а положительные числа и большой и малой «полуосями» эллипса.

4. Выясним, как выглядит часть эллипса, расположенная в первой координатной четверти.

Возьмем в первой координатной четверти произвольную точку , тогда. Следовательно, функциямонотонно убывает отдо 0, есливозрастает от 0 до.

Учитывая свойства 1- 4, построим изображение эллипса (рис. 88):

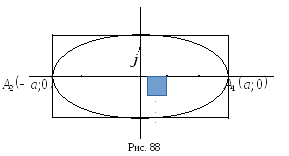
Число называетсяэксцентриситетом эллипса. Так как для эллипса , то. У окружности. Приуменьшается «высота» эллипса.

Директрисами эллипса называются две прямые, параллельные второй оси и отстоящие от нее на расстоянии .

Уравнения директрис:

или ;

или (рис. 89).

У окружности , следовательно, она не имеет директрис.

Эллипс обладает следующим директориальным свойством: для любой точки , принадлежащей эллипсу, отношение расстояния отдо фокуса к расстоянию отдо соответствующей директрисы равно эксцентриситету, т.е.

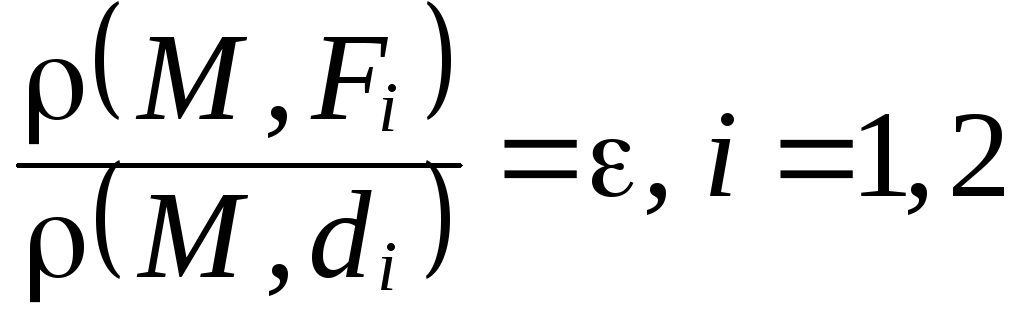(рис. 89).

Рис. 89

З

амечание 1. Так как , то. В случае, когда, фокусы эллипса будут лежать на оси, а директрисы будут параллельны оси.

Замечание 2. Директрисы эллипса не имеют общих точек с эллипсом.