Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный университет телекоммуникаций им. проф. М.А. Бонч-Бруевича

Предмет:

Цифровая обработка сигналов

Файл:

lektsii_TsOS_gruppa_RK_01 (1)

.pdf

Скачиваний:

Добавлен:

15.03.2015

Размер:

13.32 Mб

Скачать

☆

1 / 81 2 3 4 5 6 7 8 > Следующая >>>

- 1 -

Лекция 1

Раздел1. Цифровая обработка сигналов.

Под обработкой сигналов подразумевается совокупность методов и средств, целью которых является изучение свойств самих сигналов и создание сигналов с заданными свойствами. Методы и средства обработки сигналов подразделяются на аналоговые и цифровые.

Недостатки аналоговых средств и методов обработки сигналов:

•громоздкость;

•большое энергопотребление;

•зависимость характеристик от большого количества внешних факторов (нестабильность);

•ограниченность способов обработки сигналов и невозможность создания алгоритмов с высокой степенью точности;

•невозможность использования вычислительной техники. Цифровой обработкой сигналов называется область науки и

техники, в которой изучаются общие для ряда дисциплин средства и методы обработки сигналов на основе идей вычислительной математики с применением ЭВМ. Общая идея цифровой обработки сигналов иллюстрируется схемой, изображенной на рис.1.1.

(t		(n)	y(n)	y(t)
(t	АЦП	(n)	y(n)	y(t)

Рис.1.1. Цифровая обработка сигналов (АЦП – аналого-цифровой преобразователь; ЦП – цифровой процессор;

ЦАП – цифро-аналоговый преобразователь).

Аналого-цифровой преобразователь предназначен для преобразования аналогового (непрерывного) сигнала x(t) в дискретный или цифровой сигнал x(n).

Цифровой процессор служит непосредственно для цифровой

обработки сигнала.
Цифро-аналоговый	преобразователь	предназначен		для
преобразования дискретного или цифрового			сигнала	y(n) в
аналоговый (непрерывный) сигнал y(t).

Аналоговым сигналом называется электрическое колебание, которое может быть описано непрерывной или кусочно-непрерывной функцией времени х(t). Аргумент и функция могут принимать произвольные значения в определённом интервале t1, t2 и х1, х2

cоответственно, т.е.
t [t1, t2], х(t) [х1, х2].	(1.1)

Дискретный сигнал получается из непрерывного при его дискретизации без потери информационной емкости сигнала.

- 2 -

Достоинства цифровой обработкой сигналов:

•многофункциональность (ЦП может обеспечить обработку сигналов по любой программе и переключаться с одной программы на другую)

•оптимальные возможности адаптации , то есть подстройки программы;

•максимальные возможности использования вычислительной техники;

•малые габариты и низкое энергопотребление;

•полная повторяемость параметров, то есть независимость от внешних факторов;

•возможность создания алгоритмов, недоступная в аналоговой обработке сигналов (создание фильтров с абсолютно

линейной ФЧХ).

Недостатки цифровой обработкой сигналов:

•обработка сравнительно низкочастотных сигналов;

•шумы квантования могут привести к недопустимым явлениям;

•зависимость скорости обработки сигналов от сложности и точности алгоритмов.

1.1. Дискретизация непрерывных сигналов

Дискретизацией непрерывных сигналов называется процесс замены этих сигналов последовательностью их значений, отстоящих друг от друга на некоторый интервал времени Δt, называемый интервалом дискретизации или интервалом квантования.

Интервал дискретизации при условии сохранения информационной емкости сигнала должен выбираться в соответствии с теоремой В.А.Котельникова, т.е. интервал квантования Δt определяется неравенством

t ≤	1	,	(1.2)
	2F
	B

где FB – верхняя граничная частота спектра непрерывного сигнала.

Квантование непрерывных сигналов подразделяется на:

•квантование по времени,

•квантование по значению,

•смешанное квантование.

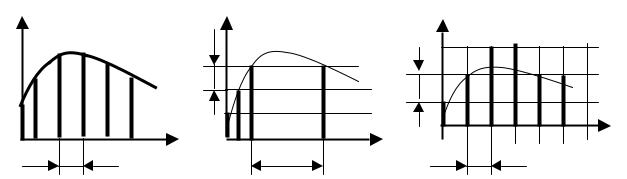
Квантованием по времени называется представление непрерывного сигнала совокупностью его значений в отдельные, равноотстоящие друг от друга, моменты времени tn=nT, где n=0,1,2,…, Т – интервал квантования или интервал дискретизации (рис.1.2,а).

При этом значения сигнала в эти моменты времени могут принимать любую величину в заданном интервале х1, х2. Соседние значения отсчетов отличаются друг от друга на некоторый интервал

- 3 -

Δх, называемый ступенью квантования. В этом случае при равномерном интервале квантования ступень квантования оказывается неравномерной.

(t)	t)
	х
	t
а)	б)

в)

Рис.1.2. Квантование непрерывных сигналов (а – квантование по времени, б

– квантование по значению, в – смешенное квантование).

Квантованием по значению называется представление непрерывного сигнала совокупностью его отсчетов, значения которых совпадают только с фиксированными уровнями в заданном диапазоне значений х1, х2, отличающих друг от друга на некоторую величину Δх, называемой ступенью квантования (рис.1.2,б). В этом случае при равномерной ступени квантования интервал квантования по времени оказывается неравномерным.

При смешанном квантовании непрерывный сигнал представляется совокупностью отсчетов в фиксированные, равноотстоящие друг от друга, моменты времени. При этом значения отсчетов принимают величину ближайшего (сверху или снизу) к значению непрерывного сигнала в этот момент времени разрешенного уровня (рис.1.2,в).

Сигнал оказывается квантованным и по времени, и по уровню. В этом случае при равномерном интервале квантования ступень квантования тоже оказывается равномерной.

При квантовании по времени или по значению полученную совокупность отсчетов называют дискретным сигналом. Однако дискретным сигналом чаще называют совокупность отсчетов, полученную при равномерном квантовании по времени.

Совокупность отсчетов, полученная при смешанном квантовании, называется цифровым сигналом.

Итак, дискретный сигнал описывается некоторой решётчатой функцией х(nТ), n = 0, 1, 2 … , значения которой определены только

при дискретных, равноотстоящих друг от друга значениях независимой переменной. Отсчёты дискретного сигнала могут принимать значения в определённом интервале уровней х1, х2:

х(nT) [х1, х2].

Выборки берутся с постоянным интервалом Т, называемом интервалом или периодом дискретизации. Поэтому величину fд = 1/T

- 4 -

называют частотой дискретизации. При этом предполагается, что

х(nТ) = 0 при n < 0.

(nT

(n)

0 2 3 4

0 1 2 3

а)

б)

в)

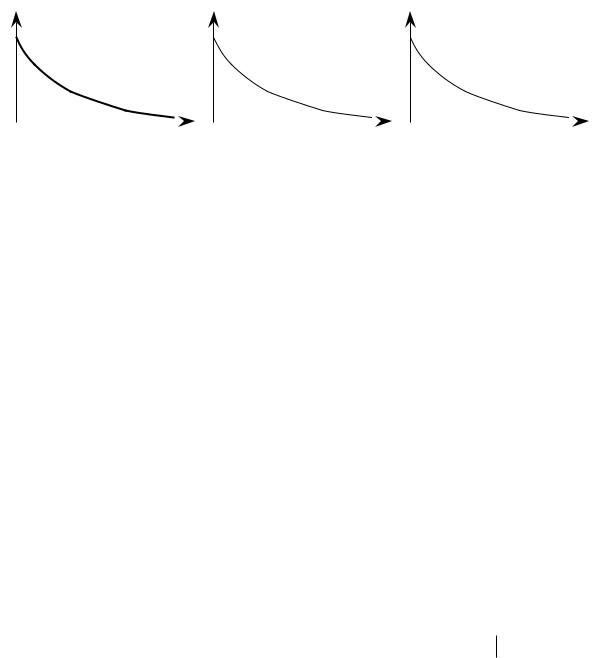
Рис.1.3. Аналоговый (а) и дискретные (б,в) сигналы

На рис.1.3 приведены графические изображения аналогового сигнала х(t) = е – а t, а > 0 (а) и соответствующего дискретного сигнала х(nТ) = е – α n T (б,в), n = 0, 1, 2 … Значения дискретного сигнала х(nТ)

называются отсчётами сигнала. Они представляют собой выборки исходного аналогового сигнала в моменты времени t = n T, п = 0, 1, 2 …,

т.е.

x(nT ) = x(t)	t=nT	при n = 0,1,2,3,....	(1.3)
	t=nT

1.1. Основы Z-преобразования.

Пусть дана непрерывная функция х(t); ей можно поставить в соответствие некую функцию Х(р): x(t) X ( p) ; где р – комплексная

переменная: р = С + j ω; С – постоянная величина, ω – текущая частота.

Х(p) и x(t) связаны парой преобразования Лапласа, т.е.

∞			1		c+ j∞
X ( p) = ∫ x(t) e−pt dt и	x(t) =		1		∫ X ( p) e pt dp
X ( p) = ∫ x(t) e−pt dt и	x(t) =	2	j	π	∫ X ( p) e pt dp	,	(1.1.1)
0		2	j	π	C− j∞
0					C− j∞

где

Х(р) – изображение функции х(t); х(t) – оригинал функции Х(р). Запишем дискретный сигнал в виде x(nT ) = x(t) t =nT .

Так как площадь каждого отсчёта дискретного сигнала равна 0, то изображение дискретного сигнала также будет равно нулю. Поэтому введём новую функцию:

	∞
	y(t) = x(t) ∑δ (t − nT )	(1.1.2)
	n=0
	∞
или	y(t) = ∑ x(nT ) δ (t − nT )	(1.1.3)
	n=0
От этой функции уже можно взять преобразование Лапласа, так
как площадь	δ (t − nT ) равна 1, а площадь x(nT ) δ (t − nT )		равна
			равна

x(nT ) :

- 5 -
∞ ∞
L{y(t)}= ∫∑ x(nT ) δ(t − nT ) e− p t dt .	(1.1.4)
0 n=0

Меняя порядок суммирования и интегрирования, получим

∞	∞
L{y(t)}= ∑ x(nT ) ∫δ (t − nT ) e−p t dt .		(1.1.5)
n=0	0
∞
Поскольку ∫δ (t − nT ) e− p t dt = e− pnT ,то получаем дискретное
0
преобразование Лапласа
	∞
D{x(nT )}= ∑ x(nT ) e− p n T .		(1.1.6)
	n=0
Обозначаяe p T = z , получим
∞
X (z) = ∑ x(nT ) z −n .		(1.1.7)
n=0

Последнее выражение представляет собой прямое Z – преобразование дискретного сигнала.

Функция X(z) называется изображением дискретного сигнала x(nT), называемого оригиналом.

Z - преобразование ставит в соответствие оригиналу {сигналу x(n)} его изображение X(z). Это соответствие взаимно-однозначное в комплексной z – плоскости.

Три преобразования L, D и Z связаны между собой важными соотношениями:

L{y(t)}= D{x(nT )}		z=e	pT = Z{x(nT )}	= X (z) .		(6.1.8)
		z=e

	Связь Z - и р - плоскостей
Так как p=C+jω, то z = e(C+ j ω) T = eC T e j ω T					или
z == eC T cos(ω T ) + j eC T sin(ω T )
Учитывая z = e p T = ξ + j η, получим
ξ = eC T cos(ω T ),						(6.1.9)
η = eC T sin(ω T ).						(6.1.9)

В полярных координатах: z = ρ e j ϕ , где ρ = 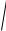ξ 2 + η2 ,

ϕ = arctg η .

- 6 -

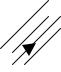
Рассмотрим p- и z – плоскости. р – плоскость

π/T

- π/T

z - плоскость

- 1

Рис.1.4. Связь p- и z – плоскостей.

В таблице 1.1 приведены некоторые точки и области р – плоскости и их отображение в z– плоскости.

Таблица 1.1.

№		р				z
1.	0					1
2.	C = −∞,ω = 0					0
3.		ˆ		π		± j
			2
	ξ = 0,ω = ±
4.	ξ = 0, ω = ±		π			Точка c координатами -1,0
			T

5.	ξ = 0, −π < ω < π					Точки на окружности
		T			T	единичного радиуса
6.	С > 0 (правая					Точки вне окружности
	полуплоскость)					единичного радиуса

7.	С < 0 (левая					Точки внутри окружности
	полуплоскость)					единичного радиуса

Свойства Z-преобразования

При описании свойств Z – преобразования будем считать, что Т =

Тогда х(nT) = х(n) 1) Линейность:

M	M
M	X (z) = ∑am X m (z) ,
Пусть x(nT ) = ∑am xm (n) , тогда	X (z) = ∑am X m (z) ,	(1.1.10)
m=1	m=1

где am - постоянные коэффициенты, Xm(z) – изображение x(nT).

Z - преобразование от суммы дискретных сигналов равно сумме Z - преобразований от каждого дискретного сигнала в отдельности.

2) Сдвиг во временной области (задержка).

- 7 -

Если изображение х(n) равно Х(z), то Z–преобразование последовательности х(n - no) при любых положительных no равно

X (z) z −n0 :

Z{x(n − n )}= z−n0 X (z) .						(1.1.11)
Докажем эту теорему.		0
Докажем эту теорему.
Z{x(n − n )}= X				∞
Z{x(n − n )}= X			1	(z) = ∑ x(n − n ) z−n	.	(1.1.12)
0			1	0	.	(1.1.12)
				n=0
Введём замену переменных: n − n0 = k , откуда n = k + n0 .
∞		−(n0 +k )
Тогда X1 (z) = ∑ x(k)	z	−(n0 +k )		или
Тогда X1 (z) = ∑ x(k)	z			или
n=0
∞
X1 (z) = z −n0 ∑ x(k) z −k				= X (z) z −n0		(1.1.13)
n=0
И окончательно
X1 (z) = X (z) z−n0 .						(1.1.14)
Сдвиг дискретного сигнала на n0 отсчётов приводит к умножению

на z −n0 в z - плоскости.

3) Теорема о свертке:

∞		X (z) = X 2 (z) X1 (z).
Если x(n ) = ∑ x1(m) x2 (n − m) , то		X (z) = X 2 (z) X1 (z).
m =0
Докажем эту теорему.
	∞	∞
Пусть X1( z ) =	∑ x1(n ) z −n , а X2 ( z ) = ∑ x2 (n ) z −n .
n =0		n =0
∞	∞
X( z ) = ∑ ∑ x1(m) x2 (n − m) z −n .			(1.1.15)

n =0 m =0

Выражение (6.1.15) можно переписать в виде:

∞	∞
X (z) = ∑ x1 (m) ∑ x2 (n − m) z −n .		(1.1.16)
m=0	n=0

Учитывая свойство задержки, выражение (1.1.16) примет вид:

	∞
	X (z) = ∑ x1 (m) z −m X 2 (z)	(1.1.17)
	m=0
	∞
или	X (z) = X 2 (z) ∑ x1 (m) z −m .	(1.1.18)
	m=0
И окончательно
	X (z) = X 2 (z) X1 (z).	(1.1.19)

- 8 -

Z - изображение свёртки двух дискретных сигналов равно произведению Z-изображений этих сигналов.

1.1.2. Обратное Z-преобразование

По Z – изображению последовательности можно однозначно определить оригинал. Формально обратное Z – преобразование определяется соотношением

x(n) =	1	∫ X (z) z n−1dz ,		(1.1.20)
	2 π j
		C
где С – контур в области сходимости			X (z)z n−1 ,	охватывающий

начало координат Z-плоскости. Обычно это окружность единичного радиуса в плоскости Z.

Способы вычисления обратного Z-преобразования:

•прямое вычисление интеграла с использованием теоремы о вычетах;

•разложение X(z) на простые дроби и использование

таблицы соответствия оригиналов и изображений.

Теорема о вычетах

Если известно изображение Х(z) некоторого дискретного сигнала x(n), то

x(n) = ∑Re sk {X (z) zn−1},

(1.1.21)

k =1

где К – число корней знаменателя (полюсов) функции X(z),

Re sk {X (z) zn−1} = lim(z − zk ) X (z) z n−1 .

(1.1.22)

Пример

z→zk

X (z) =

; корень знаменателя

= a ;

−1

1− a z

z − a

x(n) = lim(z − a)

zn−1 = lim zn = an .

z − a

z→a

Разложение Х(z) на сумму простых дробей

x(n ) = ∑ A

X (Z) = ∑

Если

, то

k .

k =1 1− a z−1

k =1

1.1.3.Типовые дискретные сигналы.

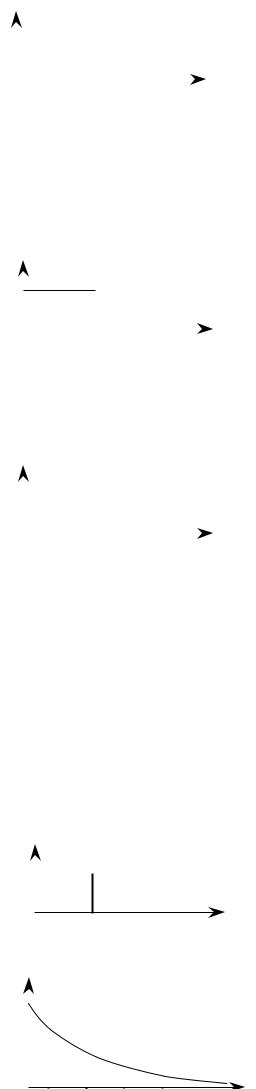
1)Единичный цифровой импульс:

		- 9 -	U0(n)
1, n = 0
1, n = 0
u0 (n) =	,	(1.1.22)		n
u0 (n) =	,	(1.1.22)		n
0, n ≠ 0

С учетом определения u0 (n) , изображение единичного

цифрового импульса будет определяться в виде:

∞

X (z) = ∑u0 (n) z −n = 1.

n=0

2)Единичный цифровой импульс, сдвинутый на m тактов:

1, n = m		u0(n-m)
1, n = m
u0 (n − m) =	. (1.1.23)	1
u0 (n − m) =	. (1.1.23)	1
0, n ≠ m				n
Найдем изображение этого импульса
∞			m
X (z) = ∑u0 (n − m) z −n .			(1.1.24)

С учетом свойства задержки или определения (1.1.23) X (z) = z−m .

3) Цифровой единичный скачок:			U1(n)
1, n ≥ 0
1, n ≥ 0
u1 (n) =	.	(1.1.24)	1	n
u1 (n) =	.	(1.1.24)	1
0, n < 0

Найдем изображение цифрового единичного скачка при условии mod z−1 1, которое будет иметь вид:

∞

X (z) = ∑u1 (n − m) z−n .

Слагаемые этой суммы представляют собой бесконечно

убывающую геометрическую прогрессию			со знаменателем z −1,
сумма которой равна	1
X (z) =		.	(1.1.25)
	1 − z−1

4) Цифровой единичный скачок, сдвинутый на m тактов:

1,n ≥ m

U1(n-m)

U1(n − m) =

(1.1.26)

0,n < m

С учетом свойства задержки

X (z) =

z−m .

−1

1− z

5) Цифровая экспонента:

(n)

- 10 -

an , n ≥ 0

x(n) = 0, n 0 , a 1. (1.1.27)<

Изображение этого дискретного сигнала

∞ ∞

описывается уравнением X (z) = ∑an z−n = ∑(a z−1 )n , (1.1.28)

0 0

слагаемые которого представляют собой бесконечно убывающую

геометрическую прогрессию со знаменателем q = a z−1. Сумма этой

прогрессии

1
X (z) =		.	(1.1.29)
	1− a z−1
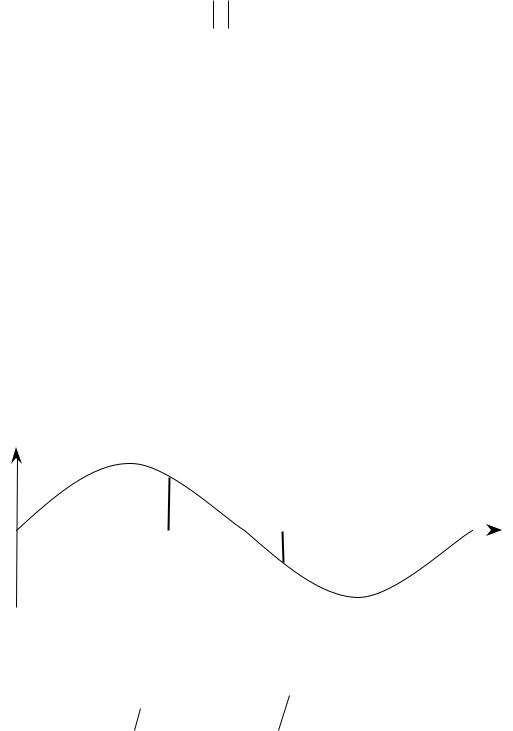
6. Цифровой гармонический сигнал.
Запишем непрерывный гармонический сигнал
x(t) = A sin(2 π f t) .
Тогда цифровой гармонический сигнал

(n )			x(nT ) = x(t)			t=nT	= A sin(2 π f n T ) .						(1.1.30)
						t=nT

							7	8	9	10	11	12	t


0	1	2	3	4	5	6
0	1	2	3	4	5	6

В цифровой обработке сигналов принципиально то, что все расчеты проводятся для нормированных частот. Нормирование проводится по частоте дискретизации.

Так как T = 1 fд , то f T = f

fд = f - нормированная частота.

fд

[

]

Если

, где fд – частота дискретизации, то f

0;0,5

и ω [0;π].

Нормирование частоты позволяет производить исследование свойств цифровых цепей и сигналов в одной и той же полосе частот, причем, если нормированные частоты различных сигналов совпадают, то их нормированные спектры тоже одинаковы.

Рассмотрим пример.

Пусть даны два цифровых гармонических колебания с частотами:

1 / 81 2 3 4 5 6 7 8 > Следующая >>>

Соседние файлы в предмете Цифровая обработка сигналов

#
15.03.2015212.21 Кб346DSP_5.pdf
#
15.03.2015188.08 Кб287DSP_6.pdf
#
15.03.2015320.69 Кб375DSP_7.pdf
#
15.03.2015232.49 Кб329DSP_8.pdf
#
15.03.2015220.6 Кб360DSP_9.pdf
#
15.03.201513.32 Mб76lektsii_TsOS_gruppa_RK_01 (1).pdf
#
15.03.2015190.53 Кб37Lek_1.pdf
#
15.03.2015120.46 Кб40Lek_2.pdf
#
15.03.2015143.87 Кб36LR-3 AT.doc
#
15.03.20151.14 Mб119метода цос.pdf
#
15.03.2015174.08 Кб296Ответы на вопросы 1.doc