Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный университет телекоммуникаций им. проф. М.А. Бонч-Бруевича

Предмет:

Цифровая обработка сигналов

Файл:

DSP_3

.pdf

Скачиваний:

449

Добавлен:

15.03.2015

Размер:

285.08 Кб

Скачать

☆

Лекция 3. Z-преобразование

1.Преобразование Лапласа.

2.Z-преобразование.

3.Основные свойства Z-преобразования.

4.Обратное Z-преобразование.

5.Связь комплексных p- и z-плоскостей. Смысл нормированной частоты.

6.Таблица соответствий.

3.1. Преобразование Лапласа

Преобразование Лапласа:

X(p) x(t)e ptdt ,

где:

x(t) — функция непрерывного времени (оригинал);

X(p) — ее изображение по Лапласу (L-изображение);

Общее правило: оригинал обозначается строчной, а его изображение той же заглавной буквой.

p — оператор Лапласа:

p j

(3.1)

Преобразование Лапласа справедливо в области абсолютной сходимости интеграла.

В теории линейных аналоговых систем оно позволило:

1)ввести фундаментальное понятие передаточной функции;

2)получить соотношение вход/выход в виде системы алгебраических уравнений.

При переходе t nT имеем дискретное преобразование Лапласа:

X(epT ) x(nT)e pnT .

n 0

Не применяется в теории ЦОС, т. к. невозможно получить передаточную функцию в дробно-рациональном виде.

3.2. Z-преобразование

Выполнив замену переменных в дискретном преобразовании Лапласа:
		z epT	,		(3.2)
получим формулу прямого Z-преобразования:


	X(z) x(nT)z n			,.	(3.3)
		n 0
где x(nT) x(n) — функция дискретного времени — оригинал; X(z)					— его z-

изображение.

Z-преобразование справедливо (3.3) в области абсолютной сходимости ряда:

| x(nT)z n | ,

n 0

называемой областью сходимости z-изображения.

3.3.Основные свойства Z-преобразования

1.Линейность — если последовательность равна линейной комбинации последовательностей, то ее z-изображение равно линейной комбинации z- изображений данных последовательностей:

x(n) a1x1(n) a2x2(n) ...

X(z) a1X1(z) a2X2(z) ...

Доказательство следует из определения (3.3).

2.Теорема о задержке — z-изображение последовательности, задержанной на m отсчетов, равно z-изображению не задержанной последовательности,

умноженному на z m :

x(n)	X(z) ,

x(n m)	X(z)z m.

Доказательство:

Найдем z-изображение задержанной последовательности по формуле (3.3):

	x(n m)z n
	n 0
Выполним замену переменных: k n m			n k m:
		z m
x(k)z (k m)		z m	x(k)z k
(k m) 0			k m
	1			z mX(z).
z m	x(k)z k	x(k)z k		z mX(z).
k m		k 0

3.Теорема о свертке — z-изображение свертки равно произведению z-изображений сворачиваемых последовательностей:


x(n) x1(m)x2(n m)	X(z) X1(z)X2(z).
m 0

Доказательство:

Найдем z-изображение свертки по формуле (3.3):

		n .
x1(m)x2(n m) z		n .

n 0 m 0

Изменим порядок суммирования:


x1(m) x2(n m)z		n	X2(z) x1(m)z m X2(z)X1(z).
m 0				m 0
m 0	n 0			m 0

3.4. Обратное Z-преобразование

Точная формула:

x(n) 1 X(z)zn 1dz,

2 j C

где C — замкнутый контур на комплексной z-плоскости, охватывающий начало координат и особые точки (полюсы) дробно-рациональной функции X(z).

Способы вычисления обратного Z-преобразования

1. На основе теоремы Коши о вычетах:

x(n)

где αk — k-й полюс, а Resαk

Resαk X(z)

K	n 1
	n 1	,
Resαk X(z)z		,
k 1

— вычет в k-м полюсе:

zn 1 lim (z αk )X(z)zn 1 .

z αk

Пример 3.1

Задано z-изображение X(z) 1 a1z 1 . Найти оригинал x(n).

а) X(z) отображается относительно положительных степеней z —

числитель и знаменатель умножается на z:

X(z)

;

z a1

б) определяются полюсы — в данном случае один:

α1 a1 ;

в) определяются вычеты — в данном случае один вычет:

Res

X(z)zn 1

lim

(z a )

zn 1

a n .

α1 a1

z a1

1 z a

a n

(3.4)

1 a z 1

2.С помощью разложения на простые дроби.

Дробно-рациональная функция X(z) может быть представлена в виде суммы простых дробей, если порядок числителя меньше порядка знаменателя:

		M 1	A
	X(z)		k			,	(3.5)
	X(z)			1		,	(3.5)
			1 k z	1
		k 1	1 k z
где αk — k-й полюс, (M 1) — количество					полюсов, Ak		— константа
разложения при k-м полюсе.
Согласно свойству линейности Z-преобразования и (3.4) имеем оригинал:
			M 1
		x(n) Ak kn					(3.6)

k 1

3.С помощью таблицы соответствий, которая будет получена в разд. 3.6.

3.5.Связь комплексных p- и z-плоскостей. Смысл нормированной

частоты

Используя (3.2) и (3.1), получаем:

z epT e( j )T e Tej T ;

z epT e Tej .

Комплексная переменная z может быть представлена в двух формах:

алгебраической:

z j ,

где e T cos ; e T sin .

jω	p	jη	z
	σ		ξ
	0		0

Рис. 3.1. Комплексные p- и z-плоскости

показательной:

z rej .

(3.7)

(3.8)

(3.9)

Сравнивая с (3.7), имеем:

r e T ; .

Вывод: нормированная частота (рад) — это угол на комплексной z-плоскости, измеряемый в радианах.

Связь комплексных p- и z-плоскостей

1.Начало координат p-плоскости:

z epT e Tej T 1ej0.

Вывод: начало координат p-плоскости отображается в точку z 1.

jω		p	jIm			z
jω		p	jIm			z
		σ		0		Re
						Re
	0				1

Рис. 3.2. Отображение начало координат p-плоскости на z-плоскость

2.Точки p-плоскости p j :

z epT e Tej T 1e j

Вывод: две точки		p j			отображаются в одну точку z 1.
Вывод: две точки		p j			отображаются в одну точку z 1.
				T
	jω				p		jIm
			π				jIm
	j		π				z
	j
		T
					σ		Re
							0
		0					0
						1

j π

Рис. 3.3. Отображение точек p-плоскости j на z-плоскость

3.Отрезок на оси частот p-плоскости j p j :

z epT e Tej T 1ej T ,

Вывод: отрезок j

p j

длиной

отображается в единичную

окружность.

jω

jIm

0 1

Рис. 3.4. Отображение отрезка p-плоскости j p j на z-плоскость

T T

4.Ось частот p-плоскости j p j :

z epT e Tej T 1ej T ,

Вывод: Ось частот p-плоскости отображается в единичную окружность с бесконечным числом оборотов.

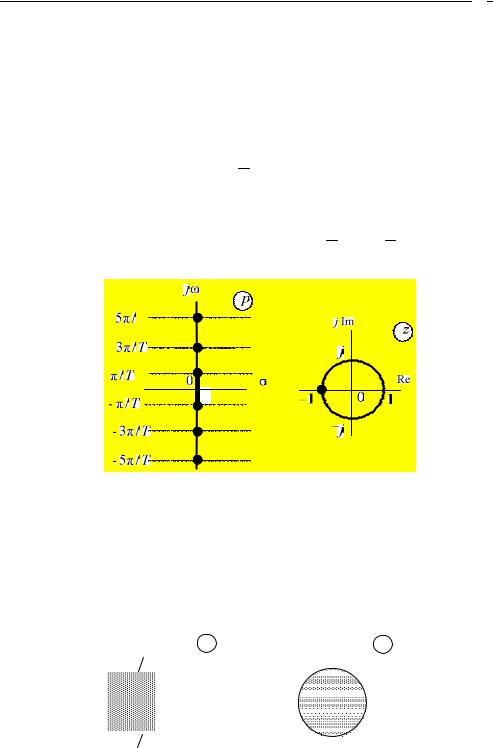
Неоднозначность отображения точек p-плоскости на z-плоскость

Множеству точек на p-плоскости (рис. 3.5):

p jk , k 1,3,5,...

соответствует одна точка на z-плоскости z epT e Tej T 1e jk 1.

Однозначное отображение — внутри коридора j p j , где z

T T

(один оборот единичной окружности).

Рис. 3.5. Отображение точек p-плоскости на z-плоскость

5. Коридор в левой p-полуплоскости: 0,			j		j		:
				T
						T
z epT e Tej T		r 1 и		.
	re j , где

Вывод: Коридор в левой p-полуплоскости отображается в единичный круг, а коридор в правой p-полуплоскости — область вне единичного круга.

jω	p		jη		z
jω	p		jη		z
π T			j
	σ				ξ
	0	1		0	1
-π T			j

Рис. 3.6. Отображение левой p-полуплоскости на z-плоскость

3.6. Таблица соответствий

Пример 3.3

Найти z-изображение цифрового единичного импульса u0 (n) .

U0(z) u0 (n) z n 1.

n 0

Пример 3.4

Найти z-изображение последовательности h(n) ( a1)n и область его сходимости.

Изобразить карту нулей и полюсов.

H(z) h(n) z n

( a )n

z n

a z 1

1 a z 1

n 0

Область сходимости:

a z 1

Для определения нулей и полюсов z-изображение выражается относительно

положительных степеней z!

H(z) .

z a1

Нули z i — это значения z, при которых z-изображение обращается в ноль.

Полюсы z k — это значения z, при которых знаменатель z-изображения обращается в ноль.

z 1 0.

z 1 a1 .

Карта нулей и полюсов — это символическое изображение нулей и полюсов на z-

плоскости одновременно с единичной окружностью.

Пример 3.5:

z-изображение

h(n) r

sin (n 1)

Найти

последовательности

и область его

sin

сходимости. Изобразить карту нулей и полюсов.

H(z) h(n) z n

rn sin (n 1) z n

n 0

sin n 0

j(n 1)

2jsin n 0

n 0

2jsin

n 0

rej z 1

e j

re j z 1

2jsin

n 0

Область сходимости:

z 1

Продолжение вычисления

e j

H(z)

2jsin 1 rej z 1

1 re j z 1

ej r z 1 e j r z 1

(1 rej z 1)(1 re j z 1)

2jsin

Нули и полюсы (числитель и знаменатель умножаем на z2 ):

H(z)

(z rej )(z re j )

z 1,2 0

z 1,2 re j

Карта нулей и полюсов:

Продолжение вычисления

H(z)

1 2rcos z 1 r2z 2

1 a z

1 a

z 2

Таблица соответствий

№

Последовательность

z-изображение

n 0;

U0 (z) 1

u0 (n)

n 0

H(z)

h(n) ( a)n

1 az 1

h(n) rn

sin (n 1)

H(z)

sin

1 a z

1 a

z 2

a1 2rcos

r a2

arccos

Пример 3.6

Найти оригинал по z-изображению H(z)

0,2 0.5z 1

. Учесть ННУ.

1 0,7z 1

Изобразить карту нулей и полюсов.

В таблице имеем соответствие:

H(z)

h(n) ( a )n ( 0,7)n

1 a

z 1

1 0,7z 1

На основании свойства линейности и теоремы о задержке:

h(n) 0,2( 0,7)n 0,5( 0,7)n 1.

С учетом ННУ:

0,2( 0,7)n, n 0

h(n)

0,2( 0,7)n 0,5( 0,7)n 1, n 0

Нули, полюсы и карта нулей и полюсов (самостоятельно):

z 1 2,5; z 1 0,7.

Пример 3.7


Найти оригинал по z-изображению H(z)	1 z 1		z 2		. Учесть ННУ.
		1 0.64z		2
1 0.8z

Изобразить карту нулей и полюсов.

В таблице имеем соответствие:

H(z)	1		1
H(z)	1 a z 1	a z 2	1 0,8z 1 0,64z 2
	1	2

Определим r и :

h(n) rn sin (n 1) sin

r 0,8

	a		0,8		1		2
arccos	1	arccos		arccos
	2r		2 0,8		2
						3

На основании свойства линейности и теоремы о задержке:

				2					2					2
	sin	(n 1)				sin	n				sin	(n 1)
	sin	(n 1)				sin	n				sin	(n 1)
h(n) 0,8n				3	0,8n 1				3	0,8n 2				3
h(n) 0,8n		sin	2		0,8n 1	sin		2		0,8n 2		sin	2
			2					2					2

									3
		3							3			3
С учетом ННУ:

						2
			sin	(n 1)
			sin	(n 1)
0,8n						3	,	n 0
0,8n					2		,	n 0
				sin	2
				sin
				3
						2								2
						2								2
			sin	(n 1)							sin	n
			sin	(n 1)							sin	n
		n				3	2 0,8			n 1		3			,	n 1
h(n) 0,8
h(n) 0,8					2								2
				sin	2						sin		2

													3
				3									3
						2								2						2
						2								2						2
			sin	(n 1)							sin	n					sin	(n 1)
			sin	(n 1)							sin	n					sin	(n 1)
0,8n						3	2 0,8n 1						3		0,8n 2					3	,	n 1
0,8n					2		2 0,8n 1						2		0,8n 2				2		,	n 1
				sin	2						sin		2					sin	2


				3									3					3
				3									3					3
			re j 0,8e					j	2
Полюсы z	1,2		re j 0,8e					3
	1,2

Нули (умножаем на z2 числитель и знаменатель H(z) и находим корни числителя):

z2 z 1 0

z		1	1	1	1	j	3	.
			2
1,2	2			2		2

Получены комплексно сопряженные нули. Определим их модуль и аргумент:

r	1		3			3		1
	1		3			3		1
				1;	arctg		:		arctg(	3)		;
	4		4			2		2			3
	4		4			2		2			3
		j
z	1e		3 .
1,2

Карта нулей и полюсов:

Соседние файлы в предмете Цифровая обработка сигналов

#
15.03.2015351.57 Кб369DSP_1.pdf
#
15.03.2015215.25 Кб145DSP_11.pdf
#
15.03.2015237.41 Кб498DSP_2.pdf
#
15.03.2015285.08 Кб449DSP_3.pdf
#
15.03.2015217.72 Кб405DSP_4.pdf
#
15.03.2015212.21 Кб346DSP_5.pdf
#
15.03.2015188.08 Кб288DSP_6.pdf
#
15.03.2015320.69 Кб375DSP_7.pdf
#
15.03.2015232.49 Кб329DSP_8.pdf