lektsia_2_semestr_2

Решение (5) записано для случая различных корней pk . Входящие в (5) n постоянных интегрирования определяются по известным независимым начальным условиям.

Вторая составляющая fвын(t) решения (2) называется вынужденной и представляет собой частное решение неоднородного дифференциального уравнения (1) (с ненулевой правой частью).

Вид частного решения определяется видом правой части уравнения. В частности, если правая часть f(t) - константа, то и частное решение ищется в виде константы.

Вынужденная составляющая обусловлена воздействием источников в цепи и при t искомая переменная f(t) fвын(t). Поэтому вынужденная составляющая называется установившейся и определяется как установившееся значение для искомой переменной в цепи после коммутации

Приведем рекомендуемый порядок расчета переходных процессов классическим методом.

1.Определить независимые начальные условия iLk(0-)=iLk(0+) и uCk(0-)=uCk(0+).

2.Для цепи после коммутации составить систему уравнений Кирхгофа с использованием уравнений для элементов.

3.Из полученной системы уравнений получить одно дифференциальное уравнение n-ой степени относительно искомой переменной. При этом порядок дифференциального уравнения n равно общему числу индуктивностей и емкостей, в которых можно задавать независимые начальные условия.

4.Найти решение полученного дифференциального уравнения

k 1

где fвын(t)=fуст(t) -вынужденная (установившаяся) составляющая; pk - корни характеристического уравнения; Ak - постоянные интегрирования, определяемые из начальных условий.

5.Определить Ak - постоянные интегрирования, используя независимые начальные условия iLk(0-) и uCk(0-).

Расчет переходных процессов в разветвленных цепях с одним реактивным элементом и источниками постоянного тока и напряжения

При одном реактивном элементе в цепи порядок дифференциального уравнения будет первым. Другой способ решения рассматриваемой задачи - применение общей формулы, описывающей переходные токи и напряжения в цепи первого порядка, а именно:

где f(t) - переходный ток или напряжение в цепи; А1 - постоянная

интегрирования; - постоянная времени цепи; fуст - установившееся значение искомой перменной в цепи после коммутации.

Постоянную интегрирования можно определить с помощью начального значения искомой переменной f(0-) =f(0+). Действительно, если подставить нуль в (8), то получим: f(0+) = fуст + А1 , откуда А1 = f(0+) fуст .

Таким образом, в данном случае постоянная интегрирования равна разности между начальным и установившимся (конечным) значениями искомой переменной. Решение (8) окончательно запишем в следующем виде:

Рассмотрим определение величин, входящих в (9).

а). Начальное значение f(0+) определяется из схемы для t = 0+, в которой заданы или определены независимые начальные условия uC(0+) или iL(0+). Для расчета могут быть использованы законы Кирхгофа или любые другие методы.

б). Установившееся значение fуст определяется из схемы после коммутации в установившемся режиме.

в). Постоянная времени определяется как

= R0C или = L / R0 ,

где R0 – сопротивление эквивалентного генератора внешней цепи относительно ветви с реактивным элементом (L или С).

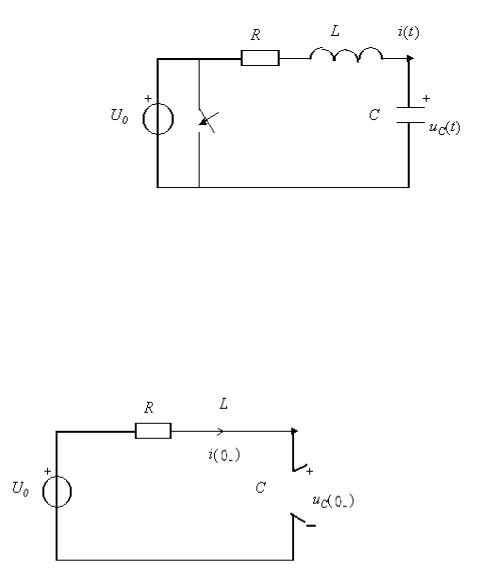
Свободные колебания в последовательном RLC-контуре

Рассмотрим свободные колебания в последовательном RLC-контуре при отключении источника постоянного напряжения на его входе (рис. 1).

рис. 1

В данном случае электрическая цепь после коммутации содержит два реактивных элемента - индуктивность и емкость. Это означает, что дифференциальное уравнение цепи должно иметь второй порядок и поэтому должны быть определены два независимых начальных условия.

рис.2

Рассмотрим цепь после коммутации:

рис.3

Согласно второму закону Кирхгофа для цепи после коммутации справедливо следующее уравнение:

Будем интересоваться напряжением на емкости uC(t) и поэтому другие напряжения, входящие в (10), а именно, напряжение на резисторе uR(t) и напряжение на индуктивности uL(t) выразим через uC(t):

После подстановки (11) в (10) получим дифференциальное уравнение:

Полученное уравнение является линейным дифференциальным неоднородным уравнением второго порядка с постоянными коэффициентами. Его решение будем искать в виде:

uC(t) = uCсв(t) + uCвын.

Для определения свободной составляющей записываем соответствующее характеристическое уравнение

LCp2 + Rcp + 1 = 0

и определяем его корни:

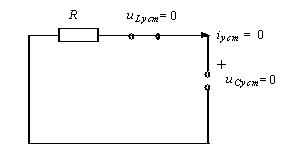
где введены следующие обозначения:

R / 2L - коэффициент затухания;

0 = 1/ LC - резонансная частота контура.

Далее записываем выражение для свободной составляющей

uСсв (t) A1ep1t A2ep2t .

Вынужденную составляющую решения определим как установившееся значение напряжения на емкости в режиме постоянного тока в цепи после коммутации (рис. 4).

рис. 4.

Из уравнения по второму закону Кирхгофа получим uCуст = uCвын = 0. Таким образом, полное решение для напряжения

Выражение для тока необходимо для определения постоянных интегрирования.

Используя нулевые начальные условия, из (14) и (15) при t = 0 получим:

uC(0+)= A1 + A2 = U0;

i(0+) = CA1p1 + CA2p2 = 0.

Решение этой системы уравнений дает выражения для постоянных интегрирования:

Таким образом, напряжение на емкости имеет следующий вид:

Выражение для тока в контуре:

Выражение для напряжения на индуктивности:

Учитывая, что p2 p1 = ( 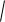2 02 )( 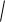2 02 ) 02 LC1 ;

Рассмотрим зависимость характера свободных колебаний в контуре от вида корней характеристического уравнения (13).

p1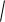,2 2 02

В зависимости от соотношения между параметрами цепи возможны следующие виды корней (13):

1)> 0 - корни вещественные, отрицательные, неравные. Режим называется

апериодическим;

2)< 0 - корни комплексные сопряженные с отрицательной вещественной частью. Режим называется колебательным;

3)= 0 - корни вещественные отрицательные, равные. Режим называется

критическим.

Далее рассмотрим эти три случая отдельно.

Апериодический режим

Условие > 0 , как нетрудно убедиться, эквивалентно соотношениям:

R > 2 и Q < 0.5,

где = L / C - характеристическое сопротивление контура,

а Q = / R - его добротность.

Таким образом, в рассматриваемом случае контур имеет значительные потери, т.е. является низкодобротным.

При этом корни (13) имеют следующий вид:

p1,2 = ,

где = 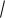2 2 < .

Корни являются вещественными отрицательными числами.

Подставляя эти корни в (14), получим решение для функции напряжения на емкости:

Качественный график полученной функции показан на рис. 5

рис.5

Переходное напряжение на емкости имеет апериодический ( неколебательный) характер и представляет из себя монотонно

возрастающую функцию. Происходит апериодический разряд конденсатора.

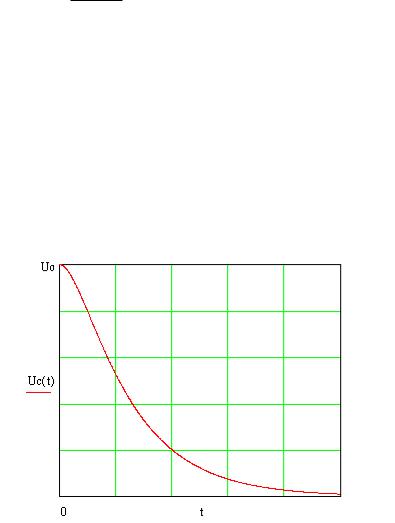
Качественные графики тока i(t) и напряжения на индуктивности uL(t) приведены ниже:

Колебательный режим

При выполнении условия

< 0

или R < 2 и Q > 0,5

корни (13) характеристического уравнения будут комплексными p1,2 = j 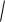20 2 = j св ,

где св = 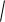02 2 - угловая частота свободных затухающих колебаний.

Запишем корни характеристического уравнения в показательной форме:

При подстановке этих корней в (17), учитывая, что p2 – p1= - j св-( + j св)=-2 j св

получим

U0e t 0 e j ( свt ) e j ( свt ) .

2 j св

Далее, используя формулы Эйлера для экспонент с мнимыми показателями, окончательно найдем