лекции

a0 0, 1 a1 0
		a1	a3
2				a1a2	a0 a3	0. 3 a3 2	0 a3
		a0	a2					0

При n=3 для устойчивости системы необходимо и достаточно, чтобы все коэффициенты характеристического уравнения были больше нуля и произведение средних коэффициентов уравнения (а1, а2) было больше произведения крайних (а0, а3).

4. Для уравнения четвертого порядка (n=4)

a0 p4 a1 p3 a2 p2 a3 p a4 0

кроме положительности всех коэффициентов требуется выполнение условия

3 a1a2 a3 a0 a32 a12 a4 0 .

При n=4 система будет устойчива при всех коэффициентах больших нуля и при

ai 0; i 1, n .

Т.о., для устойчивости систем не выше четвертого порядка необходимо и достаточно, чтобы все коэффициенты характеристического уравнения и определитель ∆п-1 были положительными.

Алгебраические критерии устойчивости для систем выше пятого порядка становятся трудоемкими для вычисления. Кроме того, алгебраические критерии не отражаются наглядностью, поэтому на практике широкое распространение получили частотные критерии устойчивости: критерий Михайлова, критерий Найквиста. И тот, и другой критерии базируются на принципе комплексного аргумента.

Критерий Рауса

Из коэффициентов характеристического уравнения составляют таблицу (матрицу), в первой строке (i=1) которой записаны коэффициенты уравнения с четными индексами, во второй строке – с нечетными индексами. В последних строках (i>3) помещены коэффициенты Рауса, полученные по формуле:

r ik = r i -2, k + 1 – (r i - 2, 1 r i -1, k + 1 / r i -1, 1),

где i — номер строки, k — номер столбца. Сам критерий формулируется так: автоматическая система устойчива, если. положительны все коэффициенты первого столбца таблицы Рауса

(включая а0 и а1 ).

41

Если не все коэффициенты столбца положительны, то система неустойчива. При этом число перемен знака среди этих

коэффициентов	соответствует		числу	правых	корней
характеристического		уравнения.	Алгоритм		вычисления

коэффициентов легко запрограммировать, поэтому критерий Рауса используют для анализа систем высокого порядка (n > 5) с помощью ЭВМ.

Преимуществом критериев Гурвица и Рауса является то, что с их помощью можно оценивать устойчивость как замкнутых, так и разомкнутых систем. Вывод об устойчивости при применении этих критериев делается применительно к той системе (замкнутой или

разомкнутой), уравнение которой анализируется.
Недостатком является малая наглядность.
0	2	4	… 1		…
1	3	5	… 2		…
| 31	32	33	… 3		…|
…	…	…	…	…	…
			…		…
1	2	3
Характеристическое уравнение:
( ) = 2 6 + 3 5 + 4 4 + 5 3 + 6 2 + 7 + 8 = 0
Частотные критерии устойчивости						05.05.2014
Критерий Михайлова

Критерий Михайлова относится к группе частотных критериев устойчивости. Он был сформулирован и обоснован в 1936 г. советским ученым А. В. Михайловым в работе «Гармонический метод в теории регулирования», которая получила высокую оценку и послужила началом широкого применения частотных методов в теории автоматического управления.

Критерий Михайлова так же, как критерии Гурвица и Рауса, основан на анализе характеристического уравнения системы, поэтому с его

42

помощью можно судить об устойчивости замкнутых и разомкнутых систем.

Пусть левая часть характеристического уравнения, называемая характеристическим полиномом, имеет вид:

D(p) = a0 pn+ an-1 pn-1+…+ a n-1 p+ an.

Подставим в этот полином вместо переменного р чисто мнимый корень, который в дальнейшем будем обозначать j . Тогда получим функцию комплексного переменного:

D(j ) = a0 (j )n+ an-1 (j )n-1+…+ a n-1 j + an,

которую можно так же, как амплитудно-фазовую характеристику, представить в виде суммы действительной и мнимой частей:

D(j ) = P( ) + jQ( )
Действительная часть P( ) содержит только четные степени
переменного :
P( ) = an - a n - 2 2 + a n - 4 4 - . . . ,	(4.14)
а мнимая часть Q( )— только нечетные:
Q( ) = an-1 - a n - 3 3 + a n - 5 5 - . . . .	(4.15)

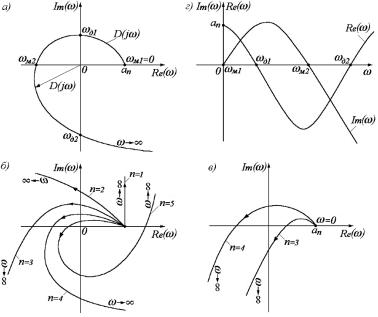
Рисунок 4.2 - Характеристические кривые (годографы) Михайлова

43

Каждому фиксированному значению переменного соответствует комплексное число, которое можно изобразить в виде вектора на комплексной плоскости. Если теперь изменять параметр от 0 до , то конец вектора D(j ) опишет некоторую линию (рис. 4.2, a), которая называется характеристической кривой или годографом Михайлова. По виду этой кривой можно судить об устойчивости системы.

Формулировка критерия Михайлова:

автоматическая система управления, описываемая уравнением п-го порядка, устойчива, если при изменении от 0 до характеристический вектор системы D(j ) повернется против часовой стрелки на угол п /2, не обращаясь при этом

в нуль.

Это означает, что характеристическая кривая устойчивой системы должна при изменении от 0 до пройти последовательно через п квадрантов. Из выражений (4.14) и (4.15) следует, что кривая D (j ) всегда начинается в точке на действительной оси, удаленной от начала координат на величину аn.

Характеристические кривые, соответствующие устойчивым системам (рис. 4.2, б), имеют плавную спиралеобразную форму и уходят в бесконечность в том квадранте, номер которого равен порядку уравнения. Если характеристическая кривая проходит п квадрантов не последовательно или проходит меньшее число квадрантов, то система неустойчива (рис. 4.2, в).

Если кривая D(j ) проходит через начало координат, то система находится на границе устойчивости. Действительно, если характеристическое уравнение имеет один нулевой корень pk = 0 (апериодическая граница устойчивости) или одну пару чисто мнимых корней pk = ± j k (колебательная граница устойчивости), то функция D(j ) при = 0 или = k обратится в нуль.

В практических расчетах удобно применять следствие из критерия Михайлова: система устойчива, если действительная и мнимая

части характеристической функции D(j ) обращаются в нуль поочередно (рис. 8.2, г), т. е. если корни уравнений P( ) = 0 и Q( ) = 0 перемежаются.

Это утверждение вытекает непосредственно из формулировки критерия Михайлова — из условия последовательного прохождения кривой D(j ) через п квадрантов.

Критерий Михайлова удобно применять для анализа устойчивости систем высокого порядка (п > 5).

44

Алгоритм применения критерия Михайлова.

1.Получаем передаточную функцию системы.

2.Составляем характеристическое уравнение системы (это знаменатель передаточной функции).

b0 pn b1 pn 1 ... bn 1 p bn 0

3. В характеристическом уравнении заменяем р на j . b0 j n b1 j n 1 ... bn 1 j bn 0

4. Выделяем действительную и мнимую часть.

p j D( j ) Re() j Im()

Re() bn bn 2 2 bn 4 4 ...

Im() bn 1 bn 3 3 bn 5 5 Re() Re() [0; )

Im() Im() ( ;0]

Действительная часть характеристического уравнения является функцией четной, а мнимая часть – нечетной. Поэтому достаточно ограничиться построением кривой, соответствующей характеристическому полиному для положительных частот. Тогда кривая, соответствующая отрицательным частотам является зеркальным отражением кривой для положительных частот относительно оси абсцисс.

5.Изменяем частоту 0; и для каждой частоты строим точку на комплексной плоскости, и соответствующий годограф характеристического уравнения.

6.Судим об устойчивости системы по критерию Михайлова.

Если годограф начинается и заканчивается на действительной оси, то система будет устойчивой, в противном случае – наоборот.

Критерий Найквиста

Критерий был сформулирован в 1932 г. американским физиком X. Найквистом, а обоснован и применен для анализа автоматических систем управления Михайловым А. В.

Критерий Найквиста позволяет судить об устойчивости системы по амплитудно-фазовой характеристике разомкнутого контура системы. В этом заключается существенное преимущество критерия, так как построение амплитудно-фазовой характеристики разомкнутого контура для большинства реальных систем оказывается проще, чем построение годографа Михайлова. Особенно упрощается это построение для одноконтурных систем, состоящих из типовых звеньев. А в тех случаях, когда неизвестно математическое описание нескольких конструктивных элементов системы, и оценка

45

их свойств возможна только путем экспериментального определения частотных характеристик, критерий Найквиста является единственно пригодным.

Основная формулировка критерия Найквиста:

автоматическая система управления устойчива, если амплитудно-фазовая характеристика W(j ) разомкнутого

контура не охватывает точку с координатами (-1; j0).

Эта формулировка справедлива для систем, которые в разомкнутом состоянии устойчивы. Таковыми являются большинство реальных систем, состоящих из устойчивых элементов.

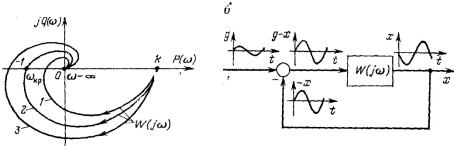
На рис. 4.3, а изображены амплитудно-фазовые характеристики разомкнутого контура, соответствующие трем различным случаям: система устойчива (кривая 1); система находится на колебательной границе устойчивости (кривая 2); система неустойчива (кривая 3).

Критерий Найквиста физически можно интерпретировать следующим образом. Предположим, что на входе системы (рис. 4.3, б) действует гармонический сигнал g (t) = gm Sin t с малой амплитудой gm. Пусть частота равна частоте , при которой фазовый сдвиг(j ), создаваемый звеном W(j ), равен — . Тогда сигнал отрицательной обратной связи окажется в фазе с сигналом g(t), и мгновенные значения сигналов будут суммироваться.

Рис. 4.3 - Амплитудно-фазовые характеристики разомкнутого контура (а) и физическая трактовка (б) критерия Найквиста

Если на частоте = , модуль | W (j ) | = 1 (нет усиления и нет подавления), то в контуре системы будут поддерживаться незатухающие колебания даже после исчезновения внешнего воздействия g (t), т. е. система будет находиться на границе устойчивости. Характеристика W(j ) при этом проходит через точку (-1; j0). Если на частоте = модуль |W(j )| < 1 (подавление есть), то после исчезновения внешнего воздействия колебания в контуре затухнут, т. е. система устойчива, характеристика не охватывает точку (-1; j0). Если

46

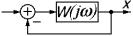
же модуль |W(j )| > 1 (усиление есть), то амплитуда сигналов в контуре будет неограниченно возрастать, т. е. система будет неустойчивой. Характеристика W (j ) в этом случае охватит точку (-1; j0).

Таким образом, особая роль точки (-1; j0) заключается в том, что она, во-первых, соответствует превращению отрицательной обратной связи в положительную, и во-вторых, является граничной между режимами усиления и ослабления сигналов звеном W (j ).

Имеется САУ:					j
W j		N
			p			;
		D			j
			p
Wзс j				W j					N p j	;
				W j					Dp j N p j
	1

D j Dp j N p j ;

здесь Dp(j ) – частотное характеристическое уравнение разомкнутой системы.

Найквист в своем критерии рассматривает вспомогательную функцию, определяемую по формуле:

j 1 W j 1

N p j

Dp j

N p j

D j

D

p

j

D

p

j

D

p

j

Примечание: Возьмем абстрактное комплексное число

A j A1 j A2

j An j

Модуль этого числа будет равен произведению модулей каждого из

множителей, а аргумент этого числа – сумме каждого из слагаемых.

mod A j

A j

A1

j

A2 j

An j

arg A j arg A1 j arg A2 j arg An j

Причем

arg

j arg D j

arg Dp j

0

0

0

.

Рассмотрим три случая.

1. Система в разомкнутом состоянии устойчива, это значит по

Михайлову:

arg Dp j n 2 ,

где п – порядок разомкнутой системы.

Частотное характеристическое уравнение разомкнутой системы также имеет порядок п, т.к. порядок числителя разомкнутой системы всегда меньше или равен порядку знаменателя разомкнутой системы

( M p j Dp j ).

47

0

Если система в замкнутом состоянии тоже устойчива, то угол одинаковый

arg D j n
0	2 .

Рассмотрим изменения аргумента при изменении частоты от 0 до

:

arg	j n		n		0
0		2		2

Система в замкнутом состоянии будет устойчива, если изменение аргумента функции (j ) при изменении частоты от 0 до составит ноль. Это возможно только в том случае, когда годограф не охватывает точку начала координат.

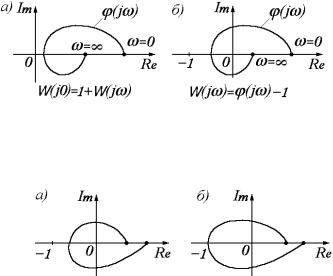
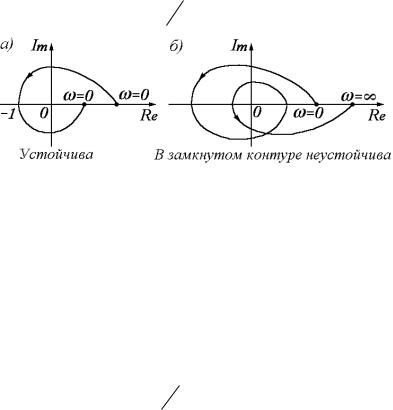
Критерий Найквиста для первого случая: замкнутая система будет устойчивой, если годограф разомкнутой системы не пересекает отрезок (- ;-1], т.е. не охватывает критическую точку (-1;0).

На рисунке а) изображен годограф системы, устойчивой в замкнутом состоянии, а на б) – системы, находящейся на границе устойчивости.

Система находится на границе устойчивости, если годограф, соответствующий амплитудно-фазовой характеристики разомкнутой системы хотя бы один раз пересечет точку [-1;0].

2. Разомкнутая система неустойчива.

Замкнутая система устойчива, это значит, что изменение аргумента

представляется формулой:

arg Dp j n 2k 2 ,

где k – количество корней характеристического уравнения разомкнутой системы, находящихся в правой полуплоскости. Изменение аргумента от 0 до :

48

arg D	p	j n
0			2 .
Изменение частоты от 0 до составит:
arg j n			n 2k		2k		k
0		2		2		2	.

При анализе устойчивой системы, при неустойчивой разомкнутой системе будем считать положительным направлением годографа – против часовой стрелки. Отрицательным направлением годографа – по часовой стрелке, или снизу вверх при пересечении действительной оси. Тогда критерий Найквиста звучит так:

если система неустойчива в разомкнутом состоянии и имеет k

положительных корней характеристического уравнения, то

система в замкнутом состоянии будет устойчива лишь в том случае, если разность между количеством положительных

переходов и количеством отрицательных переходов отрезка

( ; 1] действительной оси будет равна k/2, т.е. если годограф разомкнутой системы пересекает отрезок ( ; 1] в

положительном направлении в k 2 раз.

3. Разомкнутая система устойчива, замкнутая система неустойчива.

arg	D	p	j n ;
0			2
arg	D j n 2m				;
0				2
arg	j n 2m				n		m,
0				2		2

здесь п – количество корней замкнутой системы.

Если система в разомкнутом состоянии устойчива, а в замкнутом состоянии неустойчива, то годограф пересекает отрезок ( ; 1] в

отрицательном направлении в m 2 раз.

49

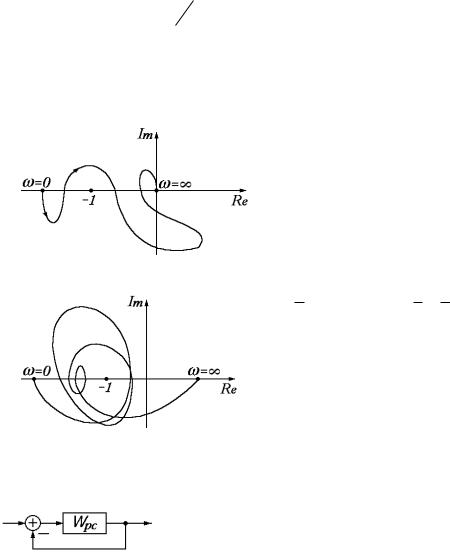
Объединяя все три случая, можно дать следующее определение критерию Найквиста:

Система в замкнутом состоянии будет устойчива, если разность между числами положительных и отрицательных переходов

годографа разомкнутой системы отрезка ( ; 1] действительной

оси	будет равна	m 2 , где т		–		количество					корней
характеристического		уравнения	разомкнутой								системы,
находящихся в правой полуплоскости.
Примеры:
1.	т=2
				1	1		1		2
				2		2			2		Система

неустойчивая.

2. т=5

12 1 1 1 1 2 12 52

Система устойчивая.

Алгоритм использования критерия Найквиста

1.Приводим систему к виду

2.Получаем передаточную функцию разомкнутой системы.

3.С помощью алгебраических критериев определяем количество (m) положительных корней характеристического уравнения разомкнутой системы.

50