
Лекция 4.
Интегрирование основных классов элементарных функций
1. Интегрирование рациональных дробей
а) Интегрирование простейших дробей
Рациональной дробью называется дробь
вида
![]() ,
где
,
где![]() и
и![]() -
многочлены. Рациональная дробь называется
правильной, если степень многочлена
-
многочлены. Рациональная дробь называется
правильной, если степень многочлена![]() ниже степени многочлена
ниже степени многочлена![]() ;
в противном случае дробь называется
неправильной. Например, дроби
;
в противном случае дробь называется
неправильной. Например, дроби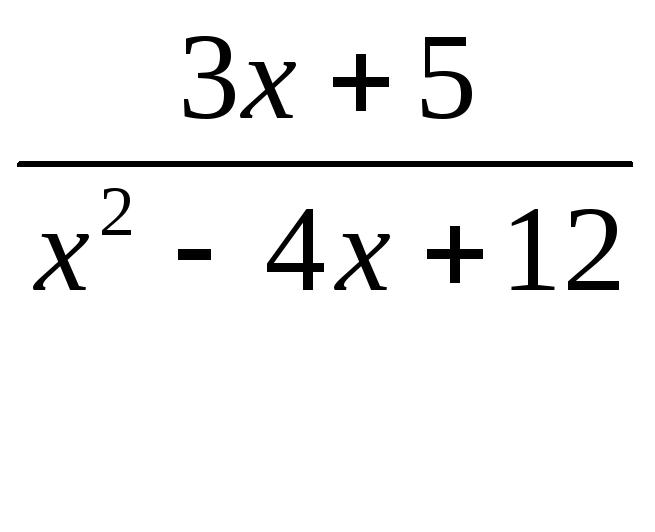 ,
,![]() - правильные, а дроби
- правильные, а дроби![]() ,
,![]() - неправильные.
- неправильные.
Простейшими (элементарными) дробями называются правильные дроби следующего вида:
 ;
; ,
гдеm
– целое число, большее единицы;
,
гдеm
– целое число, большее единицы; ,
где
,
где 0,
т.е. квадратный трехчлен не имеет
действительных корней;
0,
т.е. квадратный трехчлен не имеет
действительных корней; ,
гдеn
– целое число, большее единицы и
квадратный трехчлен не имеет действительных
корней.
,
гдеn
– целое число, большее единицы и
квадратный трехчлен не имеет действительных
корней.
Во всех четырех случаях предполагается, что А, В, p, q, а – действительные числа. Перечисленные дроби будем соответственно называть простейшими дробями I, II, III и IV типов.
Рассмотрим интегралы от простейших дробей.
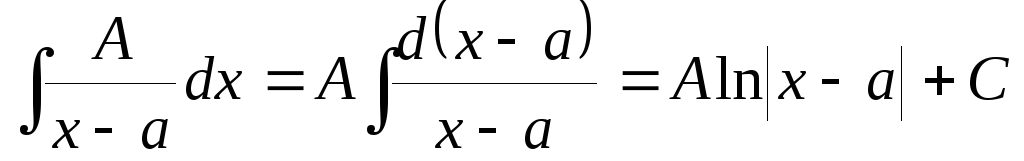 .
. ,
m=2,
3, 4...
,
m=2,
3, 4...
Вычислим далее
![]()
![]() .
.
Для этого частного случая простейшей дроби III типа получаем:
![]() ,
или
,
или![]() ,
где
,
где![]() ,
,![]() .
.
Следовательно,
![]()
![]() . ()
. ()
Для нахождения
интеграла
![]() (
(![]() 0)
выделим в числителе дроби производную
знаменателя. Так как
0)
выделим в числителе дроби производную
знаменателя. Так как
![]() ,
то числитель можно представить в виде
,
то числитель можно представить в виде![]() .
.
Тогда
![]() .
.
В первом интеграле числитель является производной знаменателя. Поэтому
![]() т.к.
т.к.![]() 0
для любого значения х.
0
для любого значения х.
Учитывая, что второй интеграл, как показано выше, находится по формуле (*), окончательно получаем:
III. ![]() .
.
Покажем теперь в общем виде, как интегрируются простейшие дроби четвертого типа:
IV.
![]()
 .
.
Выделим в числителе производную от квадратного трехчлена в знаменателе:
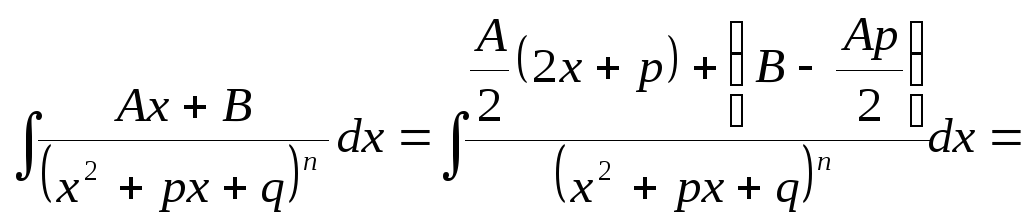
![]() .
.
Первый интеграл в
правой части равенства легко находится
при помощи подстановки
![]() ,
а второй преобразуем так:
,
а второй преобразуем так:
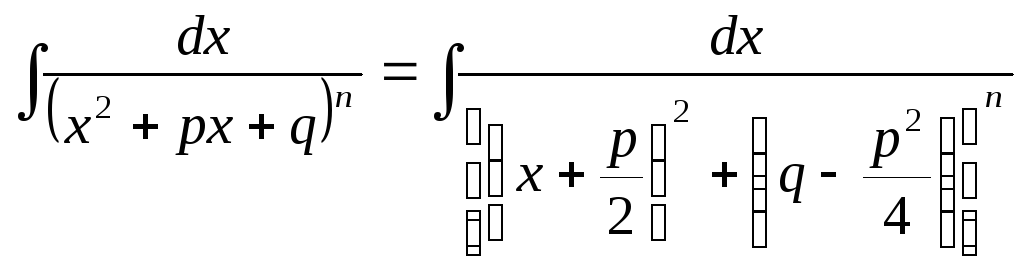 .
.
Полагая
![]() ,
,![]() и обозначая
и обозначая![]() ,
получаем:
,
получаем:
![]() .
.
Для интеграла
![]() (n
– целое положительное число), имеет
место следующая рекуррентная формула:
(n
– целое положительное число), имеет
место следующая рекуррентная формула:
![]() . (**)
. (**)
(В частном случае, при а=1 ее вывод представлен выше).
Эта формула в
результате (n-1)-кратного
применения приводит данный интеграл
In
к табличному интегралу
![]() .
.
Рассмотрим примеры.
Пример 1.
Найти
![]() .
.
Дискриминант квадратного трехчлена,
стоящего в знаменателе, отрицателен:
![]() 0,
т.е. имеем интеграл III
типа. Так как
0,
т.е. имеем интеграл III
типа. Так как
![]() ,
то числитель дроби преобразуем следующим
образом:
,
то числитель дроби преобразуем следующим
образом:![]() .
.
Поэтому
![]() .
.
Оставшийся интеграл находим выделением полного квадрата в квадратном трехчлене:
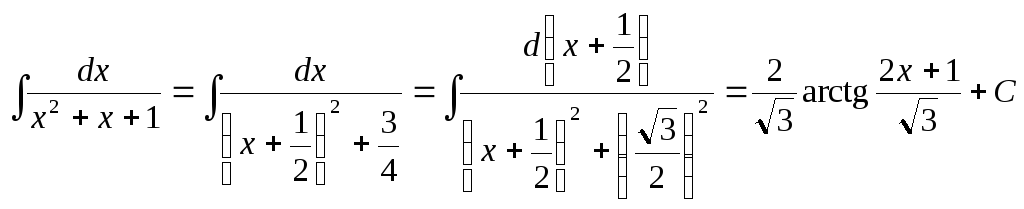 .
.
В результате заданный интеграл равен
![]() .
.
Пример 2.
Найти![]() .
.
Здесь
![]()
0, т.е. имеем интеграл IV
типа. Сначала выделим в числителе
производную квадратного трехчлена. Так
как
0, т.е. имеем интеграл IV
типа. Сначала выделим в числителе
производную квадратного трехчлена. Так
как
![]() ,
то числитель преобразуется следующим
образом:
,
то числитель преобразуется следующим
образом:![]() .
.
Далее имеем:
![]() .
.
Первый интеграл
вычисляем, положив
![]()
![]() .
.
Для вычисления оставшегося интеграла приведем его к стандартному виду, выделяя полный квадрат в квадратном трехчлене:
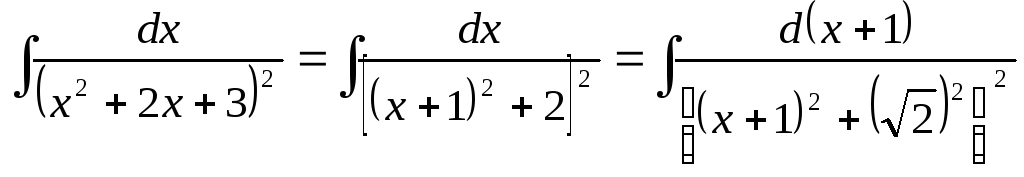 .
.
Используя рекуррентную формулу (), находим:
![]() .
.
Окончательно получаем:
![]() .
.
б) Интегрирование рациональных дробей с помощью разложения на простейшие дроби
Для интегрирования
рациональной дроби
![]() надо сделать следующие преобразования
и вычисления.
надо сделать следующие преобразования
и вычисления.
1) Если дана
неправильная рациональная дробь, то
выделить из нее целую часть, т.е.
представить в виде
![]() ,
гдеМ(х)
– многочлен, а
,
гдеМ(х)
– многочлен, а
![]() - правильная рациональная дробь.
- правильная рациональная дробь.Выделение
целой части в дроби
![]() производится
делением числителя на знаменатель
"уголком".
производится
делением числителя на знаменатель
"уголком".
Пример 3.
![]() =
=![]()
В ыделить
целую часть данной неправильной
рациональной дроби.
ыделить
целую часть данной неправильной
рациональной дроби.
х 3+3х2
+5х
+7 х![]() +2
+2
x 3 + 2х x+3+3x+1
3x 2 + 3x+ 7 х 2 +2
3х 2 + 6
3х + 1
Следовательно,
![]() .
.
2) Найти корни
уравнения
![]() и разложить знаменатель дроби на линейные
и квадратичные множители:
и разложить знаменатель дроби на линейные
и квадратичные множители:![]() …
…![]() …,
где
…,
где![]()
0,
0,
![]()
0, т.е. трехчлены имеют комплексно
сопряженные корни.
0, т.е. трехчлены имеют комплексно
сопряженные корни.
Представленное разложение основано на теоремах высшей алгебры. Доказывается, что каждый многочлен может быть представлен в виде произведения
![]() (*)
(*)
где
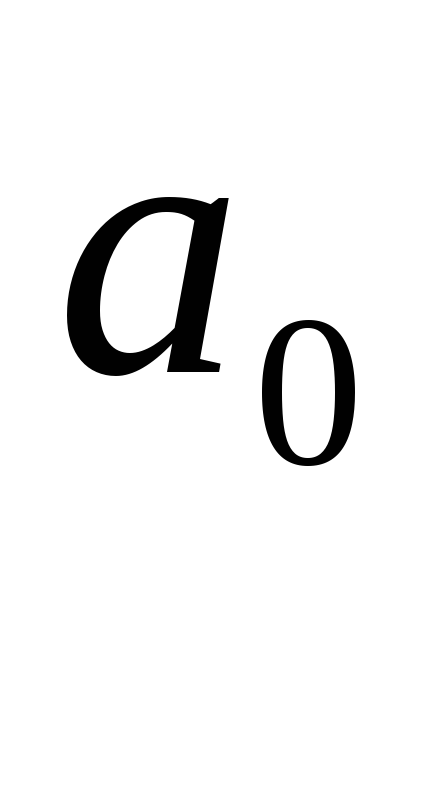 -
коэффициент при старшей степени
многочлена
-
коэффициент при старшей степени
многочлена![]() корни
уравненияQ(x)=0.
Если среди
множителей имеются совпадающие, то Q(x)
представляют в виде
корни
уравненияQ(x)=0.
Если среди
множителей имеются совпадающие, то Q(x)
представляют в виде
![]() (**)
(**)
где
![]() целые
числа, которые соответственно называются
кратностями корней
целые
числа, которые соответственно называются
кратностями корней
![]() ,причем
,причем![]() гдеn-
степень многочлена Q(x).
гдеn-
степень многочлена Q(x).
Среди корней представления (**) могут быть комплексные. Эти корни входят
сопряженными
парами
![]() и
и![]() ,где
,где![]() .
Перемножив эти два множителя, получим
.
Перемножив эти два множителя, получим
![]() где
где![]()
Таким образом, представление(**) можно записать в виде
![]() (1)
(1)
где
![]() действительные
числа.
действительные
числа.
Обозначения, используемые в(1),принимаем для удобства записи разложения (2) (см. ниже).
Пример 4.
Найти корни знаменателя правильной
дроби
![]() .
.
Легко видеть, что многочлен
![]() обращается в нуль прих
= - 1, поэтому он делится без остатка на
х+1.
обращается в нуль прих
= - 1, поэтому он делится без остатка на
х+1.
Выполним деление:
 х 3+6х
2+11х+6
х+1
х 3+6х
2+11х+6
х+1
x 3 +
х 2
x
2+5x+6
3 +
х 2
x
2+5x+6
5x 2 + 11x
5х 2 + 5х
6х + 6
6х + 6
Следовательно,
![]()
3) Правильную рациональную дробь разложить на простейшие дроби:
![]() …
…![]() …
…![]() …+
…+
![]() …
…![]()
![]() …
…![]() …
, (2)
…
, (2)
где
А1,
А2,…Ак,
В1,
В2,…В![]() ,…
К1,
К2,…Кm,…
L1,
L2,…Lm,…
M1,
M2,…Mn,…
N1,
N2,…Nn
– некоторые вещественные числа.
,…
К1,
К2,…Кm,…
L1,
L2,…Lm,…
M1,
M2,…Mn,…
N1,
N2,…Nn
– некоторые вещественные числа.
Это
разложение регулируется теоремой,
доказываемой в высшей алгебре, согласно
которой рациональную функцию
![]() ,
в которой степень многочлена числителя
меньше степени многочлена в знаменателе,
а многочленQ(x)
имеет вид (1), можно единственным образом
представить в виде (2).
,
в которой степень многочлена числителя
меньше степени многочлена в знаменателе,
а многочленQ(x)
имеет вид (1), можно единственным образом
представить в виде (2).
Примеры записи разложения правильной рациональной дроби на элементарные:
Пример 5.
![]()
Пример 6.
![]()
4) Вычислить неопределенные коэффициенты, для чего привести равенство (2) к общему знаменателю, приравняв коэффициенты при одинаковых степенях х в левой и правой частях полученного тождества и решить систему линейных уравнений относительно искомых коэффициентов.
Пример
7. Дробь
![]() разложить в сумму простейших.
разложить в сумму простейших.
Искомое разложение имеет вид:
![]() .
.
Приводя правую часть к общему знаменателю, получим тождественное равенство
![]()
Приравнивание коэффициентов при одинаковых степенях х дает систему уравнений:
![]() ,
,![]() ,
,![]() ,
откуда получаем
,
откуда получаем![]()
![]()
![]() .
.
Следовательно, искомое разложение будет иметь вид:
![]() .
.
Можно определить
коэффициенты А,
![]() ,
и
,
и![]() другим способом, придавая в полученном
тождестве переменнойх
произвольные числовые значения (в первую
очередь значения действительных корней
знаменателя Q(x)):
х
= 0, х
= 1 и, например,
другим способом, придавая в полученном
тождестве переменнойх
произвольные числовые значения (в первую
очередь значения действительных корней
знаменателя Q(x)):
х
= 0, х
= 1 и, например,
х
= -1. При х
= 0 находим А
= 4, при х = 1
получаем В2=9,
а при х
= -1 имеем
![]() ,
т.е.В1
= -3.
,
т.е.В1
= -3.
Часто бывает полезно комбинировать оба способа вычисления коэффициентов.
5) Найти интегралы выделенной целой части и всех простейших дробей, которые затем сложить.
Пример 8.
Вычислить интеграл
![]() .
.
Так как
![]() ,
то представим дробь в виде следующей
суммы:
,
то представим дробь в виде следующей
суммы:
![]() ,
т.е.
,
т.е.![]() или
или![]() .
.
Итак,
![]() .
.
Приравнивая
коэффициенты при одинаковых степенях
х
в обеих частях тождества, составим
систему уравнений:
 .
.
Решив
систему, получим
![]() ,
,![]() ,
,![]() .
.
Следовательно,
![]()
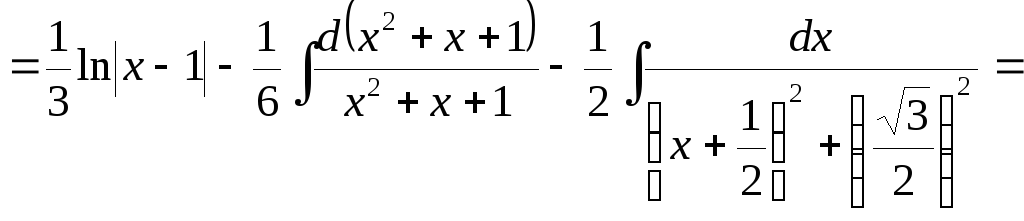
![]()
![]() .
.
В заключение отметим, что в ряде случаев возможно интегрирование рациональных дробей без разложения на простейшие дроби:

![]()
![]()
![]() .
.
Лекция 5.
