УМК

F(x)

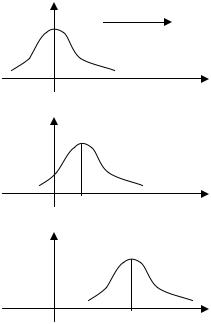
единственность, так и существование решения задачи Коши. Из формулы (1.126) непосредственно видно также, что задача поставлена корректно – при любом конечном значении t малому изменению функций f (x) и соответствует малое изменение решения.

1.26 ФИЗИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ФОРМУЛЫ ДАЛАМБЕРА

Для того, чтобы выяснить физический смысл решения (1.126), запишем функцию u(x, t) в виде суммы двух слагаемых

u1 (x, t)= ϕ (x − at) и u 2 (x, t)= ψ (x + at),

где ϕ (x)=

1

f (x)−

1

x∫F(z)dz ,

2

2a x0

ψ (x)=

1

f (x)+

1

x∫F(z)dz .

2

2a x0

И выясним смысл

u1 (x, t)

и u 2 (x, t) в отдельности.

Начнем с функции

u1 (x, t)= ϕ (x − at). Независимые переменные x и

t изменяются так, что разность остается постоянной,

т.е.

x − at = C . В таком

случае dx − adt = 0 и

dx

= a . Отсюда можно

u1

dt

a

заключить следующее. Если точка x движется

с постоянной скоростью a

в положительном

t = t0

направлении оси Ox , то смещение u1 струны в

0

x0 = at0

x

этой точке во все время движения будет равно

ϕ (C), оставаясь, таким образом, постоянным.

u1

Другими

словами,

значение

смещения

t = t1

u

1

= ϕ

(x − at) в точке x

1

в момент t

1

такое

t = t 0

x 0 .

0

же, какое было в момент

в точке

x1 = at1

x

Построим графики этой функции для

u1

возрастающих значений t :

t = t 0 = 0 ,

t = t1,

t = t2

t

= t 2 (рис. 1.4). Второй график

( t = t1) будет

сдвинут

относительно

первого

( t = t 0 )

на

0

x2 = at2

x

величину at1 , третий ( t = t 2 ) – на величину at 2

и

т.д.

Если по очереди

проектировать

эти

Рис. 1.4	рисунки на неподвижный экран,	то зритель

увидит, что график, изображенный на верхнем рисунке, «побежит» вправо. (Этот способ изображения движения положен, между прочим, в основу съемки мультипликационных фильмов).

Смещение, распространяющееся в фиксированном направлении с некоторой скоростью, называется бегущей волной. Бегущую волну,

распространяющуюся в направлении, выбранном за положительное, слева направо будем называть прямой волной.

Итак, прямая бегущая волна характеризуется решением u1 = ϕ (x − at).

Решению u 2 = ψ (x + at) будет соответствовать движение смещения

ψ (С), аналогичное указанному, но совершаемое влево. Это движение называют обратной бегущей волной.

Если взять длинную натянутую веревку и слегка качнуть ее в середине, то по веревке влево и вправо побегут волны.

	Постоянное число a =	T0	является скоростью распространения волн
		ρ
	по струне.

Таким образом, решение (1.126) задачи Коши для бесконечной струны есть сумма (суперпозиция) двух волн ϕ (x − at)+ ψ (x + at), одна из которых распространяется направо со скоростью a , а вторая – налево с той же скоростью. Это приводит к следующему графическому методу решения задачи о колебаниях бесконечной струны. Вычерчиваем кривые u1 = ϕ (x) и u 2 = ψ (x), изображающие прямую и обратную волны в начальный момент времени t = 0 , и затем, не изменяя их формы, передвигаем их одновременно со

скоростью a в разные стороны: u1 = ϕ (x) - вправо, u 2 = ψ (x) - влево. Чтобы получить график струны, достаточно построить алгебраические суммы ординат передвинутых кривых.

Формула (1.126) дает полное решение задачи. Исследуем эту формулу в

одном простом случае, когда					отсутствуют начальные скорости, т.е. когда
F(x)= 0 . Из формулы (1.126) получаем
		u(x, t)=	1	f (x − at)+		1	f (x + at).		(1.127)
			2
					2
	u				Так как функция f (x) известна, то мы
					можем вычислить u(x, t) для любых x и t .
					Пусть, например, струна в начальный
	u0				момент		времени	имеет	форму
					равнобедренного треугольника на интервале
					(− l;l ),		вне этого интервала		f (x)≡ 0 , а
− l	0	l		x	F(x)≡ 0 x (− ∞; ∞)			(рис.	1.5). Эти
					условия означают, что струна оттянута на
	Рис. 1.5
					участке (− l;l ) и в момент t = 0				без толчка

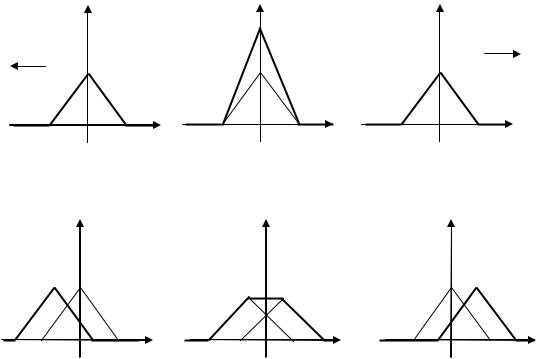
отпущена. Покажем последовательные положения струны через промежутки

	времени t =	l	. Согласно сказанному,				колебания	u(x, t) складываются из
		2a
					1					1
	двух волн: прямой u1			=		f (x + at) и	обратной	u 2	=		f (x + at). Сначала
				2					2

вычертим графики прямой и обратной волны, а затем проследим за геометрией профиля струны через указанные промежутки времени. В начальный момент t = 0 профили прямой и обратной волны совпадают (рис. 1.6), что следует из

формулы (1.127): u

1

t=0

= u

2

t=0

=

1

f (x)=

1

u

0

,

где u

0

= u

t=0

.

2

2

обратная волна

форма струны

прямая волна

u2

u

u1

u0

a

u0

u0

a

2

t = 0

t = t0 = 0

2

t = 0

A

B

− l

0

l

x

− l 0

l

x

− l 0

l

x

Рис. 1.6

u2

u

u1

u0

u0

t = t1

=

l

u0

2a

2

2

l

2

l

t =

=

2a

x1

2

−

3

l − l

l

l

x

−

3

l −

l

l

3

l

x

− l −

l

l

3

l x

2

2

2

2

2

2

2

2

Рис. 1.7

Передвинем теперь графики u1

и u 2

l

вправо и влево на расстояние

.

2

Тогда в результате сложения ординат этих графиков будем иметь форму u

	струны в момент времени t	=	l		(рис. 1.7)
			2a
		u1 и			u 2 еще раз на расстояние			l
	Передвинем графики								, в результате
						l	2
	будем иметь форму струны в момент времени t =						(рис. 1.8).

a

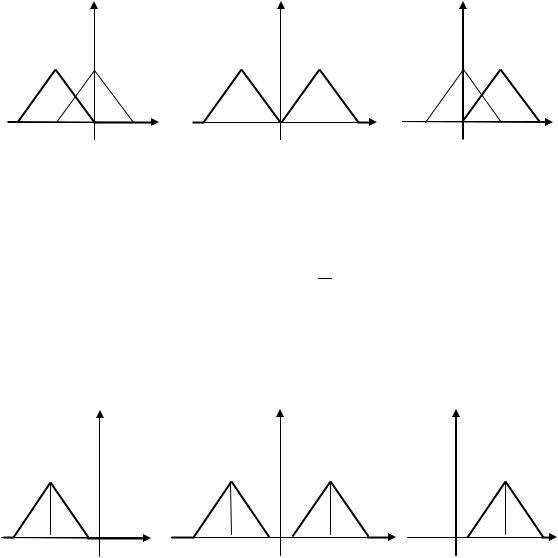
При дальнейшем перемещении графиков u1 и u 2 струна будет иметь форму, показанную на рис. 1.9, причем смещение u струны вдвое меньше, чем соответствующее смещение на участке AB .

u2

u

u1

u0

t = t2

=

l

u0

u0

a

2

2

t =

l

2

(x2 = l )

a

x − 2l − l

− 2l

− l

l

l

2l x

− l

l 2l x

Рис. 1.8

До

тех

пор,

пока t <

l

,

имеется

участок

струны,

где волны

a

накладываются друг на друга, начиная с t = l , волны начинают расходиться. В a

каждой точке струны после прохождения обеих волн (а для точек, лежащих вне области начального возмущения, после прохождения только одной волны) наступает покой. Такой процесс может наблюдаться в очень длинной струне до тех пор, пока волны, бегущие по струне, не дойдут до ее концов.

				u2									u													u1
																		t >			l
					u0								u0								a					u0
				2								2
																										2
	5								5										3					x						3			x
−		l −	3	l −		l		x −		l −	3	l −	l			l							5					l			l	5
																				l				l									l
2		2		2				2		2		2			2			2					2			2				2		2

Рис. 1.9

1.27 ЗАДАЧА КОШИ ДЛЯ ПОЛУБЕСКОНЕЧНОЙ СТРУНЫ

Метод решения задачи Коши для бесконечной струны легко применить к случаю полубесконечной струны. Пусть струна находится в состоянии покоя на положительной оси Ox и ее конец, совпадающий с началом координат, неподвижно закреплен. Тогда к уравнению колебаний струны

∂2 u	= a	2	∂2 u
∂t 2			(1.128)
			∂x 2

и начальным условиям
u		t=0	= f (x),			∂u			= F(x),	(1.129)
						∂t		t =0
заданным при x ≥ 0 , необходимо добавить еще одно граничное условие
			u		x =0	= 0.				(1.130)

Из условий (1.129), (1.130) следует, что f (0)= 0 .

Решение уравнения (1.128) при условиях (1.129), (1.130) может быть получено из формулы Даламбера (1.126) следующим образом. Допустим, что функции f (x) и F(x), определенные сначала только для x ≥ 0 , доопределены нами произвольным образом и для x < 0 . Напишем выражение u(0, t):

u(0, t)=	f (− at)+ f (at)	+	1	at∫F(z)dz .
2			2a −at
Чтобы u(0, t) было равно нулю при всех значениях
f (x) и F(x) при x < 0 определить так:
f (− x)= −f (x),		F(− x)= −F(x),

(1.131)

t , нужно функции

т.е. функции продолжить в область отрицательных значений нечетным образом. Тогда, очевидно, первое слагаемое формулы (1.131) равно нулю; второе слагаемое также обращается в нуль, потому что берется интеграл от нечетной функции в интервале, симметричном относительно начала координат. Продолжив таким образом функции f (x) и F(x) на всю числовую ось, напишем формулу Даламбера:

		f (x − at)+ f (x + at)		1	x+at
	u(x, t)=		+		∫F(z)dz .	(1.132)
	2			2a x−at

Теперь это выражение определено для всех точек x и t и при x ≥ 0 дает решение поставленной задачи. Действительно, функция (1.132) удовлетворяет уравнению (1.128), условиям (1.129) и, в силу доказанного, граничному условию (1.130).

1.28 МЕТОД ФУРЬЕ ДЛЯ УРАВНЕНИЯ СВОБОДНЫХ КОЛЕБАНИЙ СТРУНЫ

Метод Фурье или метод разделения переменных является одним из наиболее распространенных методов решения уравнений в частных

производных. Изложение этого метода мы проведем для задачи о свободных колебаниях струны, закрепленной на концах. Эта задача, как было показано в п. 1.24, сводится к решению однородного уравнения

∂2 u

= a

2 ∂2 u

(1.132)

∂t 2

∂x 2

при однородных граничных условиях

u

x =0 = 0,

u

x=l = 0

(1.133)

и начальных условиях

u

t=0

= f (x), ∂u

= F(x), (0 ≤ x ≤ l).

(1.134)

∂t

t =0

Выделим две части метода Фурье. Первая часть заключается в отыскании частных решений уравнения (1.132), удовлетворяющих граничным условиям (1.133). Вторая часть - нахождение общего решения и удовлетворение начальным условиям (1.134).

Будем искать частные решения (1.132), не равные тождественно нулю, в виде произведения двух функций

u(x, t)= X(t)T(t),

(1.135)

удовлетворяющие граничным условиям (1.133).

Дифференцируя дважды выражение (1.135) по x и по t , получим u tt = T′′(t)X(x), u xx = X′′(x)T(t ).

Подставляя найденные производные в уравнение (1.132), получим

T ′′(t)X(x)= a 2 T(t)X ′′(x)

или, деля обе части равенства на a 2 XT ,
	1 T′′(t)					X′′(x)
					=		.
	a 2		T(t)			X(x)

Последнее равенство, левая часть которого зависит от t , а правая - только от x , возможно лишь в том случае, когда обе части его не зависят ни от x ни от t , т.е. представляют собой одну и ту же постоянную. Обозначим эту постоянную через − λ (Знак числа λ будет обоснован ниже). Итак, имеем

1 T′′(t)					X′′(t)
				=			= −λ .	(1.136)
a 2		T(t)			X(t)

Из равенства (1.136) получим два обыкновенных дифференциальных уравнения

		T ′′(t)+ a 2 λT(t)= 0 ,				(1.137)
		X′′(x)+ λX(x)= 0 .				(1.138)
Таким образом, уравнение (1.132)			распалось на два уравнения, из которых
одно содержит функцию только от t , а другое						- функцию только от x или, как
говорят, в уравнении (1.132) переменные разделились.
Поскольку мы ищем решения вида (1.135), удовлетворяющие граничным
условиям (1.133), то при любом значении t должны соблюдаться равенства
u		x=0 = X(0)T(t)= 0,	u		x=l = X(l)T(t)= 0 .

Если бы обращался в нуль второй сомножитель ( T(t)≡ 0 ), то функция u(x, t)

равнялась бы нулю при	всех значениях x и	t . Такой случай интереса не
представляет. Поскольку	мы ищем нетривиальные решения, т.е. не равные
тождественно нулю, то мы должны считать, что
	X(0)= 0 и x(l)= 0 .	(1.139)

Для определения функции X(x) мы пришли к следующей краевой задаче для обыкновенного дифференциального уравнения: найти такие значения параметра λ , при которых существуют нетривиальные решения уравнения

(1.138), удовлетворяющие граничным условиям (1.139). Эту задачу называют

задачей Штурма-Лиувилля.

Те значения параметра λ , при которых задача (1.138) - (1.139) имеет нетривиальные решения, называются собственными значениями, а сами эти решения - собственными функциями.

Найдем теперь собственные значения и собственные функции задачи (1.138) - (1.139). Нужно рассмотреть три случая, когда λ < 0 , λ = 0 и λ > 0 .

Уравнение (1.138) есть линейное однородное уравнение 2-го порядка с постоянными коэффициентами. Для его решения надо составить характеристическое уравнение

k 2 + λ = 0 ;

отсюда k1,2 = ±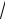− λ , следовательно, вид решения зависит от знака λ .

А. Пусть λ < 0 . Тогда корни характеристического уравнения действительны и различны и общее решение уравнения (1.138) имеет вид

X(x)= C1e 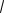−λx + C2 e−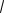−λx .

Удовлетворяя граничным условиям (1.139), получим

C + C		2	= 0
1
	−λ l				−	−λ l
			+ C	2 e				= 0.
C1e
Так как определитель этой однородной системы

1

1

=

= e− −λ l − e −λ l ≠ 0 ,

e

−λ l

e−

−λ l

единственное решение C1 = 0 и C2 = 0 .

то, как известно, система имеет

Следовательно, X(x) ≡ 0 .

Таким образом, в этом случае решений, отличных от нуля, не существует.

Б. Пусть λ = 0 . Тогда

оба

корня

характеристического уравнения равны

нулю и

X(x) = C1 + C2 x .

Граничные условия (1.139) дают:

0 = 0

C + C

1

2

C1 + C2 l = 0.

Отсюда C1 = 0 ,

C2

= 0 и, следовательно, X(x) ≡ 0 .

В.

Пусть

λ > 0 .

Корни

характеристического

уравнения мнимые

( k1,2 = ±

i ) и решение уравнения (1.138) имеет вид

λ

X(x) = C1 cos

x + C2 sin

.

λ

λ

Удовлетворяя условиям (1.139), получим

C1 1 + C2 0 = 0

λ l + C2 sin λ l = 0.

C1 cos

Из первого уравнения

следует,

что

C1 = 0 , а

из второго следует, что

l = 0 .

Последнее равенство возможно, когда C2

≠ 0 , ибо в противном

C2 sin

λ

случае X(x) ≡ 0 . Поэтому

l = 0 ,

sin

λ

=

nπ

, где n - любое целое число (n = 0, ± 1, ± 2,...).

откуда определяем

λ

l

Следовательно, нетривиальные решения задачи (1.138) - (1.139) возможны лишь при значениях

	nπ			2
λ = λn	=			.	(1.140)
		l

	Решение, отвечающее фиксированному						значению			n , обозначим через
	X n (x). Оно имеет вид					nπx
		X n (x)= C2 sin							.
	Для дальнейшего можем положить C2			= 1.			l
				nπ					2
	Итак, собственным	значениям		λn =					соответствуют собственные
							l
	функции
	X n	(x)= sin	nπx	, n =1, 2,... .						(1.141)
			l

Заметим, что в соотношениях (1.140), (1.141) мы ограничились только положительными значениями для n , так как отрицательные значения n не дают новых решений.

Обратимся теперь к отысканию функций T(t). Каждому собственному

числу λn будет соответствовать

свое решение уравнения (1.137),

которое

обозначим через Tn (t). Для функции Tn (t) имеем уравнение

T

′′(t)+

nπa

2 T (t)= 0 .

n

l

n

Общее решение этого уравнения имеет вид

T (t)= a

cos

nπat

+ b

sin

nπat

,

n

n

n

l

l

где a n , b n

- произвольные постоянные.

Таким образом, функция

(x, t)= X

(x)T (t)=

nπat

+ b

nπat

nπx

u

a

cos

sin

sin

,

(1.142)

n

n

n

n

l

n

l

l

n =1, 2,..., удовлетворяет уравнению (1.132) и граничным условиям (1.133) при

любых a n и b n .

Перейдем ко второй части метода Фурье.

При помощи собственных функций построим решения, удовлетворяющие начальным условиям (1.134).

Возьмем общее решение уравнения (1.142) в виде ряда

∞	∞		nπat			nπat			nπx
u(x, t) = ∑ u n	(x, t) = ∑ a n	cos		+ bn	sin		sin			.	(1.144)
			l			l
n=1	n =1								l
Если ряд (1.144) сходится равномерно в области								0 ≤ x ≤ l ,			0 ≤ t ≤ T , то

сумма его является непрерывной функцией в этой области. В силу однородности и линейности уравнения (1.132) ряд (1.144) будет также решением, если его можно почленно дифференцировать по X и по t . Действительно, при указанных условиях получим

		− a 2 u		∞		− a 2 u	) = 0 ,
u	tt		xx	= ∑ (u	n tt
				n=1			n xx

так как функции u n (x, t) удовлетворяют уравнению (1.132).

Далее, поскольку каждое слагаемое в (1.144) удовлетворяет граничным условиям (1.133), то этим условиям будет удовлетворять и сумма ряда, т.е.

функция u(x, t).

Остается определить постоянные a n и b n так,

чтобы функция

(1.144) удовлетворяла начальным условиям.

Продифференцируем ряд (1.144) по t :

∂u

∞

nπa

nπat

nπat

nπx

∂t

=

∑

− a n sin

+ b n

cos

sin

.

(1.145)

n =1 l

l

l

l

Подставляя t = 0 в (1.144) и (1.145), получим в силу начальных условий

(1.134):

∞				nπx			= f (x)
∑ a n sin
n =1					l
∞
							nπx	= F(x),
∑	nπa		b n		sin					(1.146)
n =1		l					l
							0 ≤ x ≤ l

Формулы (1.146) представляют собой разложение заданных функций f (x) и F(x) в ряд Фурье по синусам на интервале [0; l].

Из теории рядов Фурье известно, что всякая функция Φ(x), непрерывная на отрезке [0; l] вместе со своей производной первого порядка и удовлетворяющая условию Φ(0) = Φ(l) = 0 , разлагается в абсолютно и равномерно сходящийся ряд Фурье по синусам: