Телекоммуникационные системы

11

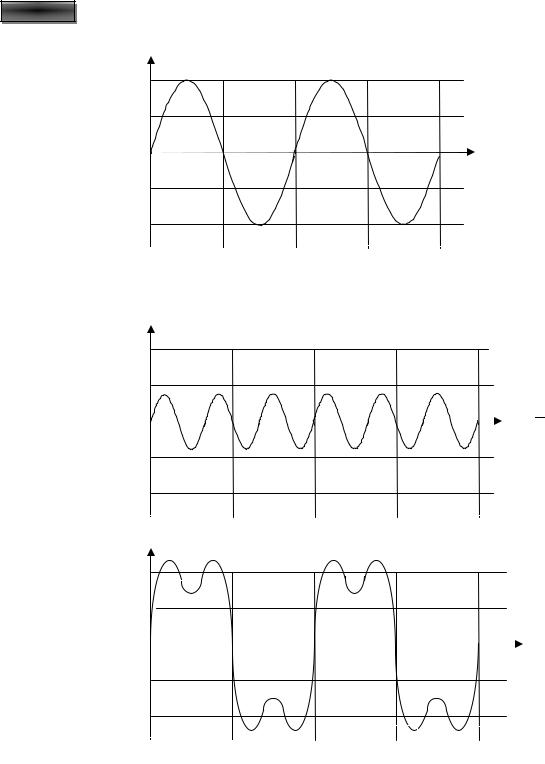
Периодические сигналы других форм показаны на рис. 1.9.

Рис. 1.9. Примеры периодических сигналов

Можно показать, что любой сигнал можно разложить на гармоники различных частот (рис. 1.10). Выражение для разложения периодического сигнала на гармонические составляющие, т.е. в ряд Фурье, имеет следующий вид:

2

cos

sin

.

1.3

Коэффициенты ряда Фурье могут быть определены по следующим формулам:

			2	/	,
	2	/		/
				cos	,
		/
		/
		2		sin	.
Итак, в общем случае периодический/					сигнал содержит не зависящую от

времени постоянную составляющую и бесконечный набор гармонических колебаний, так называемых гармоник с частотами , где 1,2,3… .

12

1.0
0.5				sin 2
0
0.5
1.0	0.5	1	1.5	2
0

1.0

0.5

0

0.5

1.0

0

0.5

1

1.5

2

1.0

0.5

0

0.5

1.0

0

0.5

1

1.5

2

Рис. 1.10. Сложение гармоник

1

3sin 2 ·3 ·

Пары коэффициентов и вместе со своими косинусными и синусными множителями являются представлением одиночного вращающегося вектора в полярной системе координат (рис. 1.11).

13

/2

cos

0

3 /2

Рис. 1.11. Графическое представление гармоники

Каждую гармонику можно описать её амплитудой				и начальной фазой
:	cos ,		sin
так, что

.

Подставив эти выражения в (1.3) получим другую форму записи ряда Фурье:

				∞	cos		.
В соответствии с	формулой				Эйлера	(			) можно
	2						cos	sin
представить ряд Фурье в комплексной∞форме:
c коэффициентами	/				∞
			1				.

/

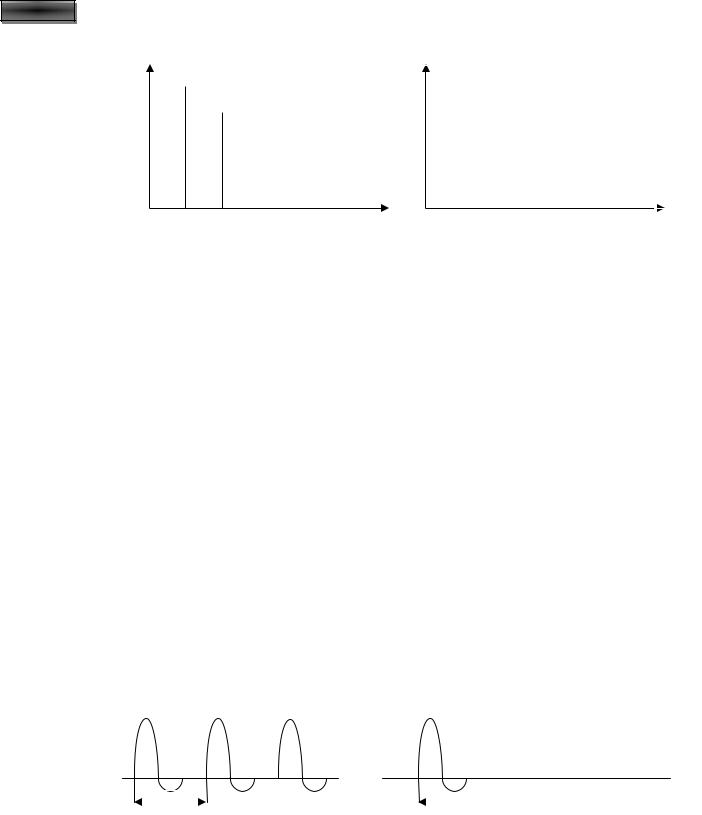
Спектральной диаграммой периодического сигнала называют графическое изображение коэффициентов ряда Фурье для конкретного сигнала. Различают амплитудные и фазовые спектральные диаграммы (рис. 1.12).

14

а

/

б

/

Рис. 1.12. Спектральные диаграммы некоторого периодического сигнала: а – амплитудная; б – фазовая

Особо интересна амплитудная диаграмма, которая позволяет судить о процентном содержании тех или иных гармоник в спектре периодического сигнала.

Рассмотренное выше представление сигналов в виде ряда Фурье справедливо для периодических сигналов. На практике часто необходимо анализировать непериодические сигналы. Обобщим ряд Фурье на случай

непериодических сигналов.
Рассмотрим сигнал				, который представляет собой периодическую
последовательность		импульсов		произвольной формы	следующих с
			пер
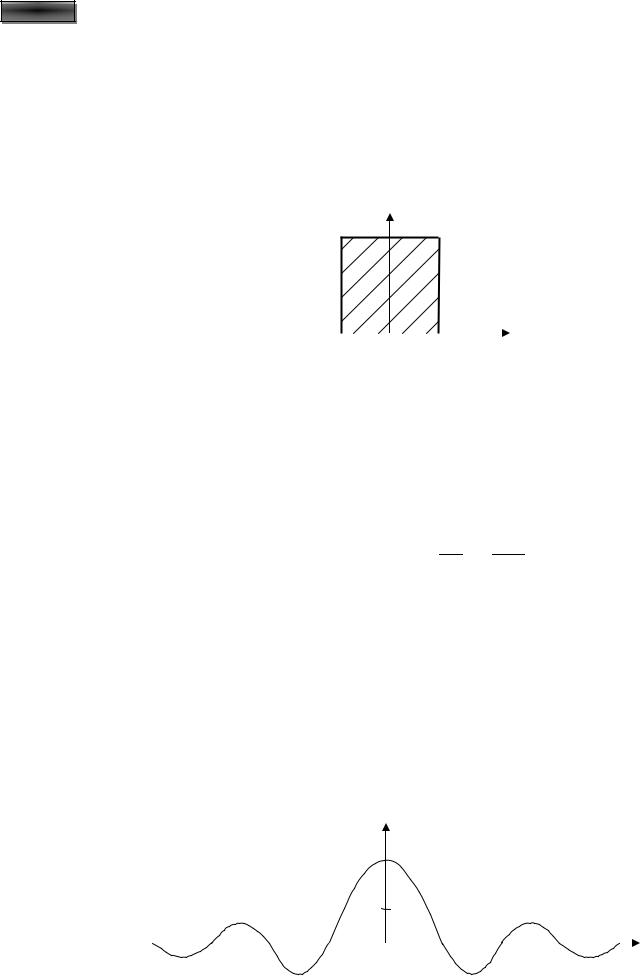
периодом (рис. 1.13). Тогда				,
			пер
где функция	описывает один импульс.

пер

……∞

а	б

Рис. 1.13. Сигналы: а – периодическая последовательность; б – одиночный сигнал

Периодическая последовательность	пер	может быть представлена в
виде комплексного ряда Фурье

15

пер

с коэффициентами

/

1

.

1.4

Чтобы

найти

соотношения для/

одиночного

импульса,

устремим к

и

∞

. При этом очевидно, что частоты

бесконечности период повторения

соседних гармоник

окажутся сколь угодно близкими,

поэтому

дискретную

переменную

1можно

заменить

непрерывной

переменной –

текущей частотой.

Учитывая,

что сигнал

на

интервале

интервала

представлен только одним импульсом

, пера за пределами этого

/2, /2

0 можно записать (1.4) в

следующем виде:

1

∞

.

1.5

При

коэффициенты

∞

зависят только от интеграла

∞

.

1.6

∞

Комплексная

функция

частоты

является

спектральной

характеристикой одиночного импульса

. Из сравнения (1.5) и (1.6) следует,

что

S kω

T

При

частота первойCгармоники.

становится бесконечно

малой.

Приращение частоты

при переходе к соседней гармонике можно

∞

отождествлять

с дифференциалом

, а вместо

можно

записать .

Подставив

и

в (1.6)получим функцию

,

1.7

∞

∞

которая носит название спектральной плотности сигнала

. Формула (1.7)

осуществляет прямое преобразование Фурье данного сигнала.

Обратное преобразование Фурье решает задачу нахождения сигнала по

его спектральной плотности

1

∞

.

1.8

2

∞

16

Спектральная плотность сигнала – это распределение энергии или

мощности по диапазону частот.
Определим		спектральную плотность прямоугольного	видеоимпульса
, показанного на рис. 1.14. Данный сигнал имеет			амплитуду ,
длительность	и	и располагается симметрично относительно начала отсчета
времени.

и/2

0

и/2

Рис. 1.14. Прямоугольный видеоимпульс

На основании формулы (1.7)

и/		и/			sin
и/	и/	cos
		и/
2	cos	2	sin	2	.

Спектральная плотность рассматриваемого сигнала есть вещественная функция частоты. Для удобства введём безразмерную переменную и/2. Тогда результат будит иметь следующий вид:

и		.	1.9

Как видно, значение спектральной плотности на нулевой частоте равно площади импульса: 0 и. График, построенный по формуле (1.9) изображен на рис. 1.15.

		1,0
			0,8
		0,6
-3π	-2π		0,4	3π
		0,2	2π
	-π		π

Рис. 1.15. График нормированной спектральной плотности прямоугольного видеоимпульса

17

Найдём спектральную плотность дельта-функции. Пусть сигнал
представляет собой	короткий импульс,		сосредоточенный в точке		и
.	А	∞		модель
имеющий площадь	. Такой	сигнал	имеет математическую	0

Спектральная плотность этого сигнала:

.

∞

На основании фильтрующего свойства дельта-функции интеграл численно равен значению функции в точке, где сосредоточена обобщённая функция. Поэтому

.

Итак, дельта-импульс имеет равномерный спектр на всех частотах. Рассматривая связь между длительностью импульса и шириной его

спектра можно сделать вывод: чем меньше длительность импульса, тем

шире его спектр.

Под шириной спектра будем понимать частотный интервал, в пределах которого модуль спектральной плотности уменьшается до некоторого уровня,

Рассмотрим| |	до	0,1| |	.
например от
	прямоугольный видеоимпульс, полагая, что верхняя
граничная частота спектра			– это частота, соответствующая первому нулю
спектральной плотности. Нетруднов				видеть, что		или			.
Можно сделать вывод,			что произведение		ширины спектра импульса на
					в и /2		в и	1

его длительность есть постоянное число, зависящее только от формы импульса

и, как правило, имеющее порядок единицы (					).	значение	для
Это	отношение	имеет	первостепенное
				в и	1

телекоммуникационных систем. Оно определяет требование к ширине полосы пропускания системы. Например, чем короче длительность импульса, тем шире должна быть полоса пропускания соответствующего усилителя. Короткие импульсные помехи имеют широкий спектр и могут ухудшать условия радиоприёма в значительной полосе частот.

1.5. Принцип корреляционного анализа

Если в трёхмерном пространстве известны два вектора	А	и , то квадрат
модуля их суммы
2 , ,

18

от угла,	между| | | |cos	– скалярное произведение этих векторов, зависящее
где

ними (рис. 1.16).

Рис. 1.16. Суммирование векторов	и
Действуя по аналогии (сигналы тоже могут быть представлены
векторами), вычислим энергию суммы двух сигналов	и :

2

Как видно, энергия суммарного сигнала содержит в себе так называемую

взаимную энергию

	2	,
т.е. скалярное произведение двух	вещественных сигналов		и
пропорционально взаимной энергии этих сигналов:
,		.

Если сигналы тождественно совпадают, то скалярное произведение становится равным энергии

,.

Рассмотрим работу импульсного радиолокатора, предназначенного для измерения дальности до цели (рис. 1.17).

Радиолокатор

Цель

Рис. 1.17. Метод измерения дальности до цели радиолокатором

19

Информация об объекте измерения заложена в величине -задержке по времени между зондирующим и принятым сигналами. Формы зондирующего

и принятого сигналов одинаковы.

Структурная схема устройства обработки радиолокационных сигналов, предназначенного для измерения дальности, изображена на рис. 1.18.

1

2 . . . N

устройство сравнения

устройство сравнения

задержка

устройство сравнения

Рис. 1.18. Устройство для измерения времени задержки сигналов

Система состоит из набора элементов, осуществляющих задержку

передаваемого (зондирующего) сигнала		на определенные отрезки времени
, ,…,	. Задержанные сигналы вместе с принятым		подаются на

устройства сравнения, действующие в соответствии с принципом: сигнал на выходе появляется лишь при условии, что оба входных колебания являются «копиями» друг друга. Зная номер канала, в котором сигналы в наибольшей мере совпали (наложились друг на друга), можно измерить задержки, а значит, и дальность до цели.

Для количественного определения степени отличия сигнала		и его
смещенной во времени копии	принято вводить автокорреляционную
функцию (АКФ) сигнала	, равную скалярному произведению сигнала и
копии:

.

При 0 автокорреляционная функция становится равной энергии сигнала:

0.

Кчислу простейших свойств АКФ можно отнести ее четность:

.

20

Действительно, если сделать замену переменных

, то

.

Важное свойство автокорреляционной функции состоит в том, что при любом значении временного сдвига модуль АКФ не превосходит энергии сигнала:

|

| | 0 |

.

Это вытекает из неравенства Коши-Буняковского:

| , | .

Итак, АКФ представляется симметричной кривой с центральным максимумом, который всегда положителен.

Найдем АКФ прямоугольного видеоимпульса. На рис. 1.19, а изображен

прямоугольный видеоимпульс с амплитудой и длительностью		. На этом же
рисунке представлена его «копия», сдвинутая во времении		в сторону
запаздывания	на . Интеграл вычисляется элементарно на	основании
графического	построения. Действительно, произведение	отлично

от нуля в пределах интервала времени, когда наблюдается наложение сигналов.

Этот временной интервал	τи |τи|. График АКФ – треугольник, изображенный
на рис. 1.19, б.

и

и

0

и

и

а б

Рис. 1.19. Нахождение АКФ прямоугольного видеоимпульса

Часто необходимо определить АКФ последовательности прямоугольных видеоимпульсов. Такие сигналы широко используются в радиолокации. Для обнаружения такой пачки и измерения положения ее во времени создают