Глава 1. Действительные функции одного переменного

1.1. Основные понятия и определения

1. Понятие функции состоит из трех частей: 1) области определения D; 2) множества T, содержащего область значений E; 3) правила, которое для каждого элемента из области D задает единственный элемент из области T.

2. Для функций действительного переменного их области определения D и области значений E принадлежат множеству действительных чисел R. Если обозначить функцию символом f, а элементы D и E- символами x и y , то функция f сопоставляет по определенному правилу каждому элементу единственное значение, что записывается в виде:

или .

По традиции x называют независимой переменной (аргументом), а y – зависимой переменной — функцией. Иногда функцию обозначают тем же символом, что и значение и пишут y=y(x).

3. Способы задания функций:1) аналитический (т.е. математической формулой, называемой аналитическим выражением и дающей возможность вычислить значение функции); 2) графический; 3) при помощи таблицы; 4) при помощи словесного описания.

4. Функция определена для , если значениеf(x) конечное и вещественное. Множество значений x, для которых функция определена, образует область определения (область существования) . В простейших случаяхD есть открытый промежуток (интервал) (a;b): a < x < b, или полуоткрытые промежутки [a,b): a  x < b, (a,b]: a < x  b, или закрытый промежуток (отрезок, сегмент) [a,b]: a  x  b, где a и b- некоторые числа или символы - и +  (в последних случаях равенства исключаются). Если функция задана аналитически и об области определения ничего не сказано, то ее считают множеством всех чисел, при которых формула, задающая значение функции, имеет смысл и называют естественной областью определения функции D(f).

5. Множество всех значений, которые функция принимает на элементах своей области определения, есть область значений .

6. Считая, что x - некоторая точка М числовой оси, а соответствующее значение y=f(x) – точка другой числовой оси, функцию называютотображением. Тогда точка -образ точки М, а точка М- прообраз точки .

7^. Сложная функция. Если функция y=f(u) отображает область определения E в область значений L, а функция u=g(x) отображает свою область определения D в область значений , при этом, тогдасложная функция

y=f(g(x)) (1.1)

отображает D в L. Запишем иначе: если и, где, то сложная функция

(1.2)

Из (1.1) и (1.2) следует т.е. функцияреализует идею: “ применяйg, затем применяй f ”.

8^. Неявная функция. Пусть дано уравнение вида и пусть существует такое множествоX, что для каждого существует по крайней мере одно числоy, удовлетворяющее уравнению . Обозначим одно из таких чисел черези поставим его в соответствие числу. В результате имеем функциюf , определенную на множестве X и такую, что для всех. В этом случае говорят, что функцияf задается неявно уравнением . Уравнениеможет задавать не одну, а некоторое множество неявно заданных функций.

9^.Основные элементарные функции: постоянная y = C (C – const); степенная ; показательная(a > 0); логарифмическая , (a > 0, ); тригонометрические,; обратные тригонометрические,,.

10^. Элементарной функцией называется всякая функция, которая может быть явным образом задана с помощью формулы, содержащей лишь конечное число арифметических операций и композиций (суперпозиций) основных элементарных функций.

11^. Классы элементарных функций.

1) Целые рациональные функции:

, . Сумма, разность и произведение целых рациональных функций есть целая рациональная функция.

2) Дробные рациональные функции: .

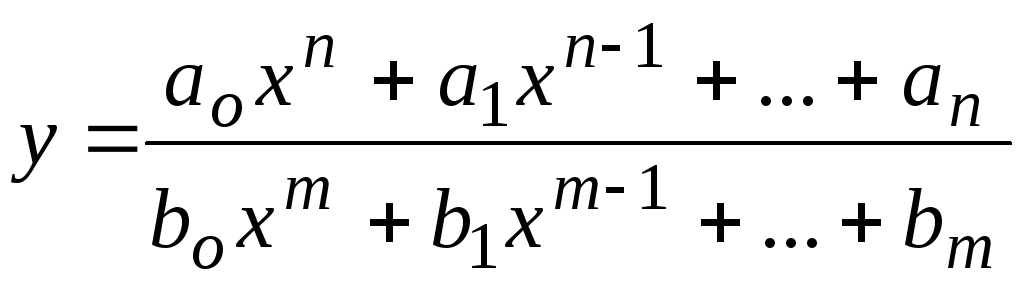Заметим, что класс целых рациональных функций содержится в классе дробных рациональных функций.

3) Алгебраические функции: между y и x существует зависимость вида

,

где -многочлены относительноx; при этом y удовлетворяет определенным требованиям. Классы 1), 2) содержатся в классе алгебраических функций.

4)Трансцендентные функции – это всякие функции, не являющиеся алгебраическими. Можно показать, что показательная, логарифмическая, прямые и обратные тригонометрические функции являются трансцендентными.

Пример. Определить область определения функций:

а) ; б).

 а) Так как функция arcsinx определена при , а функция lgx – при x>0, то x должен удовлетворять нескольким условиям одновременно, т.е. получается пересечением множеств:

;

б) Так как функция sinx определена , lgx – при x>0 и функция определена, кромеx=0, то

, .

Находим односторонние пределы:

.

Поэтому .

Пример. Сложную функцию представить цепочкой из основных элементарных функций.

 y – “пятисложная” функция. 

Пример. Функция задана в неявном виде уравнением. Написать функцию в явном виде.

 Решив уравнение относительноy, получим в явном виде две однозначные функции ис одной и той же областью существования, но с различными областями значений. Обе они удовлетворяют исходному уравнению, и выбор конкретной из них, если необходимо, определяется из геометрических, или физических, или иных соображений.