1.Прямые на плоскости

Задача аналитической геометрии – применение к геометрическим задачам координатного метода. Тем самым задача переводится в алгебраическую форму и решается средствами алгебры.

В прямоугольной декартовой системе координат каждой точке соответствует пара чисел – ее координаты.

Рассмотрим произвольное уравнение от двух переменных F(x, y) = 0. Изобразив на плоскости точки координаты которых (x, y) удовлетворяют уравнению, получим некоторую фигуру. Исходное уравнение является уравнением этой фигуры. Вместо уравнения может фигурировать неравенство или другое условие – каждое такое условие всегда можно записать в виде уравнения.

Пересечение двух фигур задается системой уравнений, определяющих эти фигуры.

Расстояние между двумя точками M₁(x₁, y₁) иM₁(x₂, y₂) определяется по формуле

. (1)

Пример 1. Построить уравнение окружности с центром в точкеА(a, b) и радиусомr.

Обозначим произвольную точку окружности через M(x, y), тогда, согласно определению, окружность задается уравнениемАМ = r. Воспользовавшись формулой (1), получаем алгебраическое уравнение, или

. (2)

Это и есть искомое уравнение окружности.

Уравнение прямой на плоскости

Прямую на плоскости можно задавать уравнениями разных видов. Для решения задач следует использовать уравнение, наиболее удобное для данной задачи.

Уравнение с угловым коэффициентом:

y = kx + b. (3)

В этом уравнении угловой коэффициент k– это тангенс угла наклона прямой к оси абсцисс. Угол отсчитывается от положительного направления оси абсцисс против часовой стрелки.

Недостаток этого уравнения: им невозможно задать вертикальную прямую x = a.

Общее уравнение прямой:

Ax + By + C = 0. (4)

Этим уравнением можно задать любую прямую. Коэффициенты А, В, Спри этом определяются не однозначно, а с точностью до пропорциональности.

Уравнение прямой в отрезках:

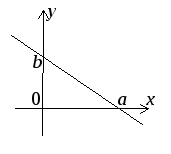. (5)

Здесь знаменатели аиb– это координаты точек пересечения прямой с соответствующими координатными осями. С помощью такого уравнения невозможно задать прямую, проходящую через начало координат или параллельную одной из осей.

Уравнение прямой, проходящей через две заданные точки M₁(x₁, y₁) и M₁(x₂, y₂):

. (6)

В этом уравнении один из знаменателей может оказаться равным 0. Тогда общее уравнение прямой получаем, приравнивая к 0 соответствующий числитель (на другую часть уравнения не обращаем внимания).

Уравнение прямой, проходящей через заданную точку M(x₀, y₀) с угловым коэффициентом k:

y – y₀ = k(x – x₀). ( 7)

Каноническое уравнение прямой:

. (8)

Здесь M(x₀, y₀) – точка, через которую проходит прямая, а (m, n) – направляющий вектор, задающий направление прямой.

Любой из приведенных видов уравнений легко преобразовать в любой другой.

Дополнительные формулы.

Угол между двумя прямыми.

Пусть прямые имеют угловые коэффициенты k₁иk₂. Тогда уголмежду ними определяется из условия

. (9)

Условие перпендикулярности двух прямых с угловыми коэффициентамиk₁иk₂:

k₁k₂= –1. (10)

Условие параллельности двух прямых с угловыми коэффициентами k₁ иk₂:

k₁=k₂ . (11)

Расстояние от точки M(x₀, y₀) до прямой Ax + By + C = 0:

. (12)

Площадь треугольникаАВСс вершинамиА(x₁, y₁), В(x₂, y₂), С(x₃, y₃):

. (13)

Пример 2. Даны три точкиА(3; 1),В(–2; 3),С(1; –2). а) Построить уравнение прямойАВ; б) Найти тангенс угла между прямымиАВиАС; в) построить уравнение перпендикуляра к прямойАВ, проходящего через точкуС; г) построить уравнение прямой, параллельнойАВи проходящей через точкуС; д) найти расстояние между точкамиАиС; е) найти расстояние между точкойСи прямойАВ; ж) найти площадь треугольникаАВС.

Решение. а) Воспользуемся формулой (6):

;

;

2x– 6 = –5y+ 5;

2x+ 5y– 11 = 0 – общее уравнение прямой.

б) Приведем уравнение прямой АВ, полученное в пункте а) к виду (3):

.

Отсюда ее угловой коэффициент . Аналогично находим угловой коэффициент прямойАС, построив ее уравнение:

;

–3x+ 9 = –2y+ 2;

3x– 2y– 7 = 0;

;

.

Теперь по формуле (9) получаем

.

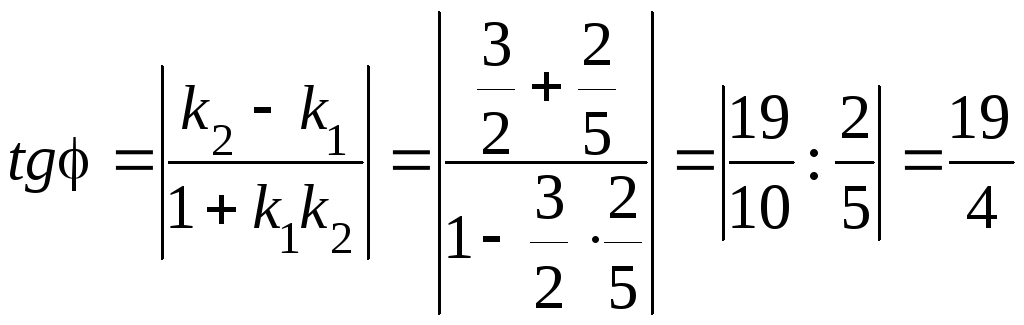в) Угловой коэффициент k₃ перпендикуляра кАВнаходим из условия (10):k₁k₃= –1, гдеиз пункта б). Отсюда. Уравнение перпендикуляра находим по формуле (7):

y– (–2) = ;

2y+ 4 = 5x– 5;

5x– 2y– 9 = 0.

г) Согласно формуле (11), угловой коэффициент прямой, параллельной АВ, также равен. Поэтому по формуле (7) получаем уравнение

y– (–2) = ;

5y+ 10 = –2x+ 2;

2x+ 5y+ 8 = 0.

д) Воспользуемся формулой (1):

.

е) Воспользуемся формулой (12) и уравнением прямой АВиз пункта а):

.

ж) Воспользуемся формулой (13):

.