Гл. Yi. Основные теоремы и некоторые применения дифференциального исчисления. § 1. Теоремы о среднем

Определение1. Точканазываетсяточкой (локального) максимума (минимума) функции, если. Точки локального максимума и минимума называютсяточками (локального) экстремума(рис. 1).

Т

Рис. 1

еорема1 (Ферма). Если функциядифференцируема в точкеи имеет в этой точке локальный экстремум, то.

Доказательство. Пусть для определенности функцияимеет в точкемаксимум, т.е.. Отсюда дляимеем, если, и, если.

Так как функция дифференцируема в точке, то это означает, что,. Следовательно,.

З

а) б)

Рис. 2

амечание. Условия теоремы Ферма только достаточные. Так для функции, но экстремума в точкенет (рис. 2а). С другой стороны, функцияимеет локальный минимум в точке, ноне существует (рис. 2б).

Поэтому в дальнейшем будем называть точки из стационарными, иликритическимидля функции, если либо в них, либоне существует.

Теорема2 (Ролль). Пусть функциянепрерывна на отрезке. Если, то в интерваленайдется, по крайней мере, одна точка локального экстремума (рис. 3). Если, кроме того, функцияf дифференцируема в интервале (a b), то

Доказательство.По теореме Вейерштрасса (гл.IY, § 2) функциядостигает на отрезкесвоих точных верхней и нижней граней. Пусть,. Тогда:. Если, то функция- постоянна, и потому любую точку интерваламожно считать точкой экстремума.

Е

Рис. 3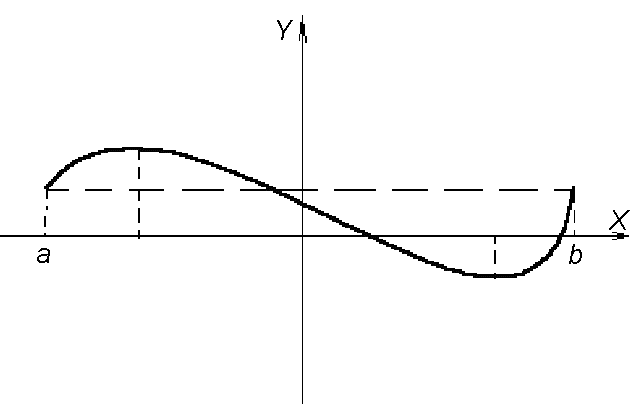

сли, то из условияследует, что хотя бы одно из значенийилине принимается на концах отрезка. Пусть этим значением является. По той же теореме Вейерштрасса. Тогда, т.е. точкаявляется точкой максимума.

Второе утверждение сразу следует из теоремы 1.

Вставка 1.

Теорема 3 (Коши). Пусть функцииинепрерывны на отрезкеи дифференцируемы на интервале, причем. Тогда

. (1)

Доказательство. Покажем сначала, что. Если бы, то функцияудовлетворяла бы условиям теоремы Ролля и, значит, нашлась бы точка, а это противоречит условию теоремы.

Рассмотрим вспомогательную функцию , где числовыберем таким образом, чтобы. Это дает, откуда

. (2)

Так как функция удовлетворяет теперь условиям теоремы Ролля, то, илиЭто дает

.

Сравнивая этот результат с (2), получим (1).

Отметим частный случай теоремы Коши.

Теорема4 (Лагранж). Пусть функциянепрерывна на отрезкеи дифференцируема на интервале. Тогда

. (3)

Вставка 2.

Полагая в (3) получим, что в условиях теоремы Лагранжа(рис. 5). Поэтому формулу Лагранжа называют ещеформулой конечных приращений Лагранжа в отличие от приближенной формулы, которая следует из определения дифференциала и иногда называетсяформулой бесконечно малых приращений.

Вставка 3.

Вопросы и упражнения.

1. Существуют ли функции, для которых нарушено одно (два, три) условие теоремы Ролля, но которые имеют экстремум?

2.Доказать теорему Лагранжа.

3.Показать, что формулу конечных приращений Лагранжа можно записать в виде, где

4.Доказать, что если все корни многочленас действительными коэффициентами вещественны, то его производные,, также имеют лишь вещественные корни.

5.Доказать неравенство.

6.Доказать, что если функцияfнепрерывна на [a;b], дифференцируема в (a;b),f(a) =f(b) и не является постоянной, то на отрезке [a;b] существуют точкис₁ис₂такие, что .

7.Привести примеры, иллюстрирующие существенность и достаточность условий теоремы Лагранжа (Коши).