
Глава IV. Непрерывность функции. § 1. Непрерывность функции в точке и точки разрыва функции.
Будем предполагать, что область определения Dfсодержит некоторую окрестностьО(х0) точких0.
Определение1. Функцияf называетсянепрерывной в точке х0, если
![]() .
(1)
.
(1)
Вставка 1.
Расшифровывая определение предела функции в точке, получим следующие определения.
Определение 2 (по Гейне). Функцияfназываетсянепрерывной
в точке х0, если{xn}Df,![]() ,
выполнено
,
выполнено
![]() .
(2)
.
(2)
Вставка 2.
Вместо (2) можно написать
![]() ,
(3)
,
(3)
т.е. для непрерывной в точке х0функции символы предела (lim) и функции (f) можно менять местами.
Определение3 (по Коши). Функцияfназываетсянепрерывной в точке х0, если> 0=() > 0:xO(x0)O(x0)|f(x) –f(x0)| <.
Вставка 3.
Пусть х=х-х0(приращение аргумента в точке х0),y=f(x) –f(x0) =f(х0+х) -f(x0) (приращение функции в точке х0).
Определение4. Функцияf называетсянепрерывной в точке х0, если
![]() .
(4)
.
(4)
Таким образом, непрерывность функции в точке означает, что б/мприращению аргумента соответствуетб/мприращение функции.
Вставка 4.
Определение5. Функцияfназываетсянепрерывной слева (справа)в точке х0, если![]() .
.
Вставка 5.
Ясно, что функция fбудет непрерывной в точкех0, если она непрерывна в ней справа и слева (см. теорему о связи между односторонними пределами и пределом функции в точке).
Из определения непрерывности функции в точке и из леммы о локальном сохранении знака функции, имеющей предел (§3, гл.III), получим утверждение.
Теорема 1 (о сохранении знака непрерывной в точке функции). Пусть функцииf непрерывны в точкех0 иf(x0)0. ТогдаО(x0):хО(x0)Df sgnf(x) =sgnf(x0).
Аналогично, из теоремы 3 (§3, гл.III) получим утверждение.
Теорема2 (об ограниченности непрерывной в точке функции). Если функцииfнепрерывны в точкех0, тоО(x0) такая, что функция будет ограничена на множествеО(x0)Df.
Теорема3 (арифметические свойства
непрерывных в точке функций). Пусть
функцииf иgнепрерывны в точкех0иС– постоянная Тогда. функцииCf,f + g,fgи![]() (еслиg(x0)0) непрерывны в
точкех0.
(еслиg(x0)0) непрерывны в
точкех0.
Доказательствонепосредственно
следует из определения непрерывности
и арифметических свойств пределов
функций. Докажем, например, непрерывность
функцииfg. Согласно
теореме о пределе произведения имеем
(пределы![]() и
и![]() существуют
в силу непрерывности функцийfиgв точкех0и равны соответственноf(x0)
иg(x0))
существуют
в силу непрерывности функцийfиgв точкех0и равны соответственноf(x0)
иg(x0))
![]() ,
,
что и означает непрерывность функции fgв точкех0.
Вставка 6.
Теорема4 (о непрерывности сложной
функции). Пусть функцияy=(x)
непрерывна в точкех0, а функцияf(y)
непрерывна в точкеy0=(х0),
причем![]() .
Тогда сложная функцияf[(x)]
непрерывна в точкех0.
.
Тогда сложная функцияf[(x)]
непрерывна в точкех0.
Доказательство. Пусть> 0 – произвольно. В силу непрерывности функцииfв точкеy0=() > 0:yDfO(y0)|f(y) –f(y0)| <.
Далее, для полученного > 0 в силу непрерывности функциив точкех0=() =() > 0:хDO( х0)|(x) -(х0)| <, т.е.y=(x)O(y0).
Таким образом, если хDO( х0), то |f(y) –f(y0)| = |f((x)) –f((х0))| <. Это и означает непрерывность сложной функцииf()в точкех0.
Вставка 7.
Определение6. Точках=х0называется точкой разрыва функцииf,если либо функцияfопределена только в![]() ,
либо определена вО(х0), но
не является непрерывной в точкех0.
,
либо определена вО(х0), но
не является непрерывной в точкех0.
Если х0 - точка разрыва функцииfи существуют конечныеf(х0), то такая точка называется точкой разрыва первого рода, а величина=f(х0+) -f(х0-) – скачком функцииfв точке х0. Если, кроме того,= 0, тох0называется точкой устранимого разрыва.
Все остальные точки разрыва функции называются точками разрыва второго рода. Если хотя бы один из пределов f(х0) равен, то разрывы называется бесконечным.
Вставка 8.
Вопросы и упражнения.
Сформулировать определение непрерывности функции в точке слева и справа по Гейне и по Коши.
Пусть функции fиg- разрывны в точкех0. Что можно сказать о функцияхfg,f + g иCf, гдеС– константа?
Пусть функция fнепрерывна в точкех0, а функцияgразрывна в точкех0. Что можно сказать о функцияхfg,f + g?
Показать, что функция
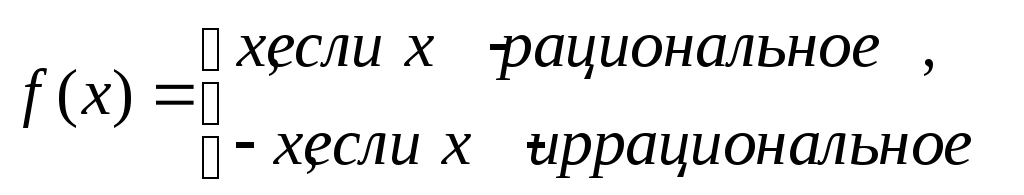 непрерывна в точкех= 0, а в остальных
точках терпит разрыв второго рода. (Л.,
149)
непрерывна в точкех= 0, а в остальных
точках терпит разрыв второго рода. (Л.,
149)Докажите непрерывность sinx в произвольной точке.
Сформулируйте на языке «-» в положительном смысле утверждение: функцияf, определенная вО(х0), не является непрерывной в точкех0.
Пусть для некоторых чисел > 0 можно найти=() > 0 такие, что
 .
Можно ли утверждать, что функцияfнепрерывна в точкех0, если:а)множество {}
– конечное;б)множество {}-
счетное;в)
.
Можно ли утверждать, что функцияfнепрерывна в точкех0, если:а)множество {}
– конечное;б)множество {}-
счетное;в)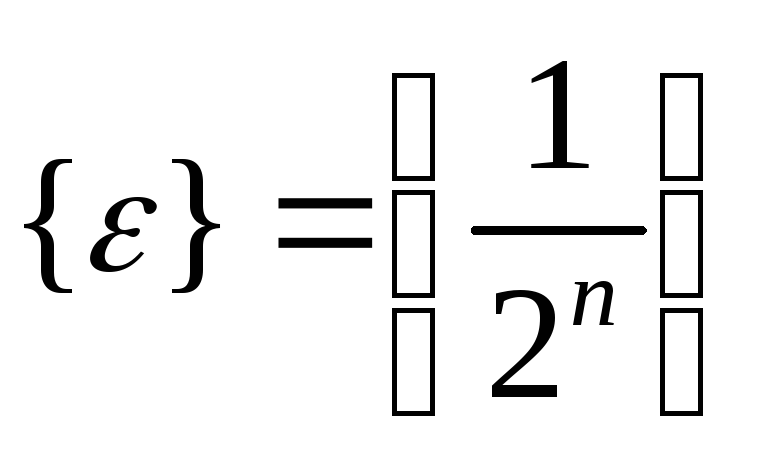 ?
?Пусть > 0=() > 0:
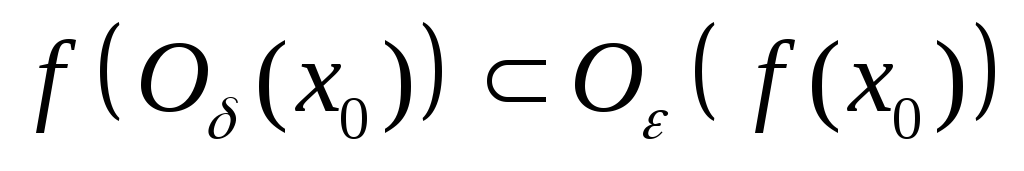 .
Следует ли отсюда, что функцияfнепрерывна в точке х0? Если
нет, то какое свойство функцииfописывается данным условием?
.
Следует ли отсюда, что функцияfнепрерывна в точке х0? Если
нет, то какое свойство функцииfописывается данным условием?При каком выборе числа афункция
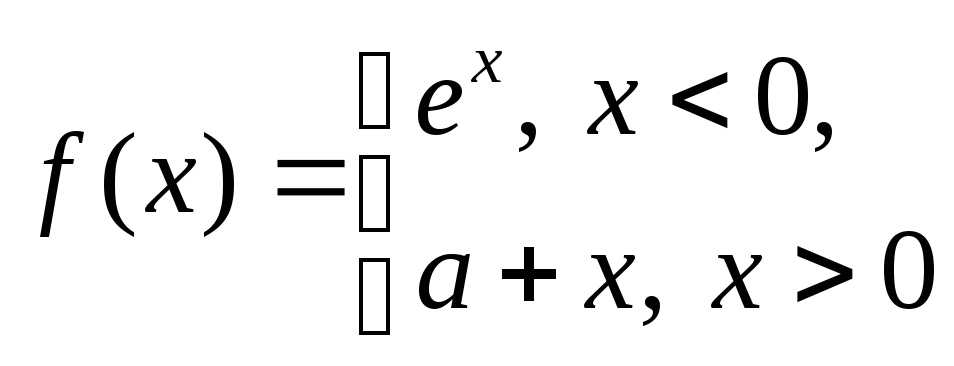 будет непрерывной в точкех= 0?
будет непрерывной в точкех= 0?Доопределить функцию
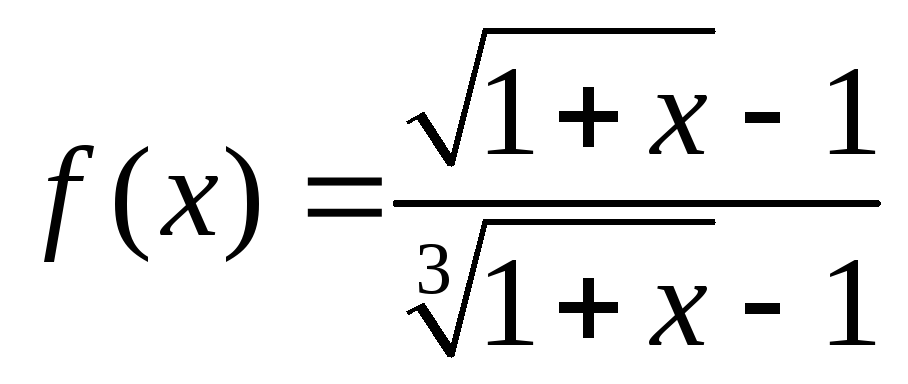 в точкех= 0 так, чтобы она была
непрерывной в этой точке.
в точкех= 0 так, чтобы она была
непрерывной в этой точке.Исследовать на непрерывность функции
 и
и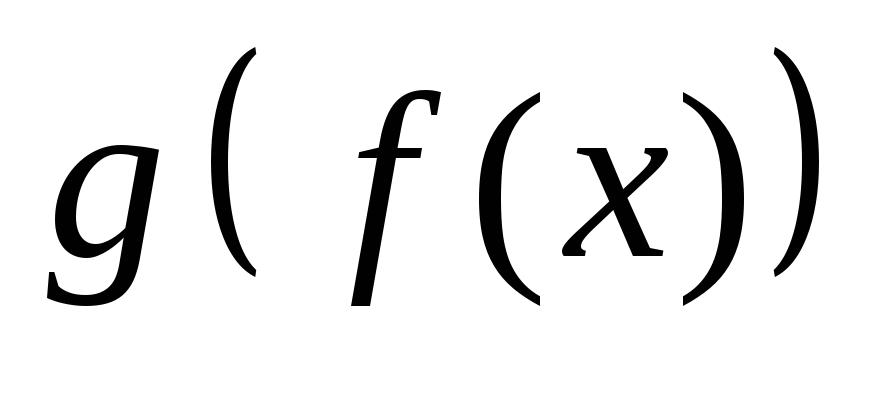 ,
если
,
если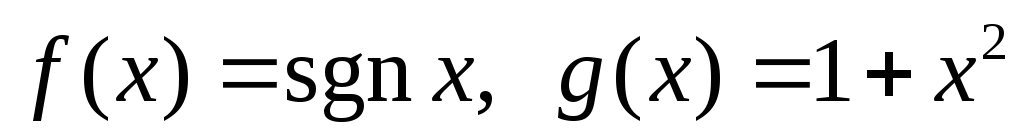 .
.
