
ГОС / 26
.doc26. Волновое движение. Интерференция и дифракция волн. Бегущие и стоячие волны. Энергия волны. Звуковые волны.
Волнами называются возмущения, распространяющиеся в среде (или в вакууме) и несущие с собой энергию. Характерное свойство волн состоит в том, что перенос энергии волной осуществляется без переноса вещества. Основными видами волн являются упругие (звуковые и сейсмические) волны, волны на поверхности жидкости и электромагнитные волны (световые и радиоволны).
В зависимости от направления колебаний частиц по отношению к направлению, в котором распространяется волна, различают продольные и поперечные. В продольной волне частицы среды колеблются вдоль направления распространения волны. В поперечной волне частицы среды колеблются в направлениях, перпендикулярных к направлению распространения волны. Упругие поперечные волны могут возникнуть лишь в среде, обладающей сопротивлением сдвигу. Поэтому в жидкой и газообразной средах возможно возникновение только продольных волн. В твердой среде возможно возникновение как продольных, так и поперечных волн.
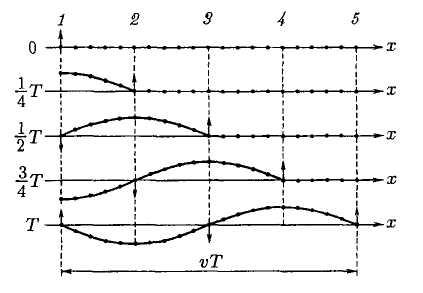
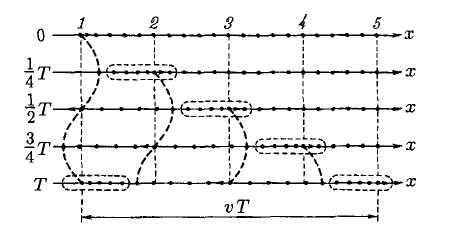
рис. 1 движение частиц при распространении в среде поперечной волны.
рис. 2. движение частицы при распространении в среде продольной волны.
Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. Волновые поверхности могут быть любой формы. В простейших случаях они имеют форму плоскости, сферы или цилиндра. Соответственно волна в этих случаях называется плоской, сферической или цилиндрической.
 Рис.
1.4
Рис.
1.4
Расстояние λ, на которое распространяется волна за время, равное периоду колебаний частиц среды, называется длиной волны.
![]() где
v
— скорость
волны, Т — период колебаний. Длину волны
можно определить также как расстояние
между ближайшими точками среды,
колеблющимися с разностью фаз, равной
2π (рис.
1.4).
где
v
— скорость
волны, Т — период колебаний. Длину волны
можно определить также как расстояние
между ближайшими точками среды,
колеблющимися с разностью фаз, равной
2π (рис.
1.4).

Уравнением волны
называется выражение, которое дает
смещение колеблющейся частицы как
функцию её координат x,
y,
z
и времени t:
![]() .
.
Э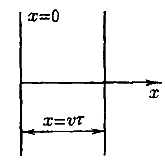 та
функция должна быть периодической как
относительно времени, так и относительно
координат. Найдем вид функции
та
функция должна быть периодической как
относительно времени, так и относительно
координат. Найдем вид функции
![]() в случае плоской волны, предполагая,
что колебания носят гармонический
характер. Для упрощения направим
оси координат так, чтобы ось х
совпала с
направлением распространения волны.
Тогда волновые поверхности будут
перпендикулярными к оси х
и, поскольку
все точки волновой поверхности колеблются
одинаково, смещение
в случае плоской волны, предполагая,
что колебания носят гармонический
характер. Для упрощения направим
оси координат так, чтобы ось х
совпала с
направлением распространения волны.
Тогда волновые поверхности будут
перпендикулярными к оси х
и, поскольку
все точки волновой поверхности колеблются
одинаково, смещение
![]() будет зависеть только от х
и t:
будет зависеть только от х
и t:
![]() .
Пусть
колебания точек, лежащих в плоскости
х = 0
(рис.), имеют вид
.
Пусть
колебания точек, лежащих в плоскости
х = 0
(рис.), имеют вид
![]() .
Найдем вид колебания точек в плоскости,
соответствующей произвольному
значению х.
Для того
чтобы пройти путь от плоскости х
= 0 до этой
плоскости, волне требуется время τ
= x/v
(v
— скорость
распространения волны). Следовательно,
колебания частиц, лежащих в плоскости
х, будут
отставать по времени на τ
от колебаний частиц в плоскости х
= 0, т. е. будут
иметь вид
.
Найдем вид колебания точек в плоскости,
соответствующей произвольному
значению х.
Для того
чтобы пройти путь от плоскости х
= 0 до этой
плоскости, волне требуется время τ
= x/v
(v
— скорость
распространения волны). Следовательно,
колебания частиц, лежащих в плоскости
х, будут
отставать по времени на τ
от колебаний частиц в плоскости х
= 0, т. е. будут
иметь вид
![]() .
.
Итак, уравнение плоской волны (и продольной, и поперечной), распространяющейся в направлении оси х, выглядит следующим образом:
![]() (1.4)
(1.4)
Величина а
представляет собой амплитуду волны.
Начальная фаза волны α
определяется
выбором начал отсчета x
и t.
Зафиксируем
какое-либо значение фазы, стоящей в
уравнении (1.4), положив
![]() (1.5)
(1.5)
Это выражение определяет связь между временем t и тем местом х, в котором фаза имеет зафиксированное значение. Вытекающее из него значение dx/dt дает скорость, с которой перемещается данное значение фазы. Продифференцировав выражение (1.5), получим
![]() (1.6) Таким
образом, скорость распространения
волны v
в уравнении
(1.4) есть скорость перемещения фазы, в
связи с чем ее называют фазовой скоростью.
(1.6) Таким
образом, скорость распространения
волны v
в уравнении
(1.4) есть скорость перемещения фазы, в
связи с чем ее называют фазовой скоростью.
Согласно (1.6) dx/dt > 0. Следовательно, уравнение (1.4) описывает волну, распространяющуюся в сторону возрастания х. Волна, распространяющаяся в противоположном направлении, описывается уравнением
![]() (1.7)
(1.7)
Уравнению плоской
волны можно придать симметричный
относительно х
и t
вид. Для
этого введем величину
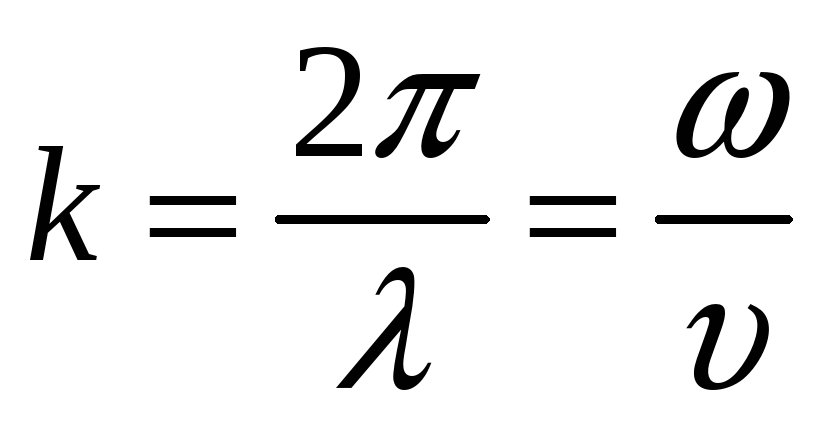 (1.8) Тогда
уравнение волны можно переписать так:
(1.8) Тогда
уравнение волны можно переписать так:
![]() (1.9)
(1.9)
Уравнение волны, распространяющейся в сторону убывания х, отличается от (1.9) только знаком при члене кх. При выводе формулы (1.9) мы предполагали, что амплитуда колебаний не зависит от х. Соответственно уравнение плоской волны с учетом этой зависимости имеет следующий вид:
![]() (1.10) (
(1.10) (![]() — амплитуда в точках плоскости х
= 0).
— амплитуда в точках плоскости х
= 0).
Уравнение плоской
волны, распространяющейся в производном
направлении, образующем с осями координат
x,
y,
z
углы α,
β,
γ:
![]()
где
![]() – волновой вектор,
– волновой вектор,
![]() – радиус вектор; или:
– радиус вектор; или:
![]() ,
,
где
![]() ,
,
![]() ,
,
![]() .
.
Стоячие волны – волны, возникающие вследствие интерференции волн, распространяющихся во взаимно противоположных направлениях. Практически С. в. возникают при отражениях волн от преград и неоднородностей в результате наложения отражённой волны на прямую. Различные участки С. в. колеблются в одной и той же фазе, но с различной амплитудой. В С. в., в отличие от бегущей, не происходит течения энергии. Такие волны возникают, например, в упругой системе - стержне или столбе воздуха, находящегося внутри трубы, закрытой с одного конца, при колебаниях поршня в трубе. Бегущие волны отражаются от границ системы, и в результате наложения падающих и отражённых волн в системе устанавливаются С. в. При этом по длине воздушного столба образуются т. н. узлы смещений (скоростей) - плоскости, перпендикулярные к оси столба, на которых смещения частиц воздуха отсутствуют, а амплитуды давлений максимальны, и пучности смещений - плоскости, на которых смещения максимальны, а давления равны нулю. Узлы и пучности смещений располагаются в трубе на расстояниях четверти длины волны, причём у твёрдой стенки образуются всегда узел смещений и пучность давлений. Во всяком объёме, имеющем определённые границы и источник звука, образуются С. в., но более сложной структуры.
Падающая волна:
![]() ,
отраженная:
,
отраженная:
![]() .
.
складываем:
![]() –
–
уравнение стоячей волны. Выбираем начало отсчета x и t так, чтобы выполнялось:
![]() ,
,
![]()
Координаты узлов
(min):
![]()
Координаты
пучностей (max):
![]()
Волновое уравнение и его решение.
Уравнение любой волны является решением дифференциального уравнения, называемого волновым. Чтобы установить вид волнового уравнения, сопоставим вторые частные производные по координатам и времени от функции
,![]() описывающей
плоскую волну. Продифференцировав
эту функцию дважды по каждой из
переменных, получим:
описывающей
плоскую волну. Продифференцировав
эту функцию дважды по каждой из
переменных, получим:
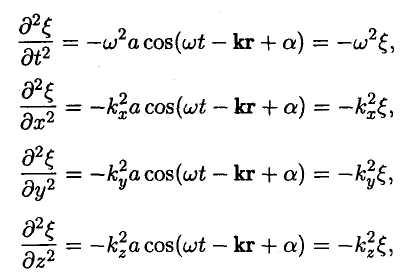
Сложение производных
по координатам дает
![]()
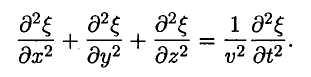 Сопоставив
эту сумму с производной по времени и
заменив
Сопоставив
эту сумму с производной по времени и
заменив
![]() на 1/v2,
получим уравнение
на 1/v2,
получим уравнение
![]() Это
и есть волновое можно записать в виде
Это
и есть волновое можно записать в виде
где Δ — оператор Лапласа.
Легко убедиться в том, что волновому уравнению удовлетворяет не только функция
![]()
, но и любая функция вида
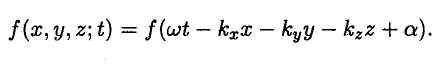
Действительно, обозначив выражение, стоящее в скобках в правой части, через ζ, имеем
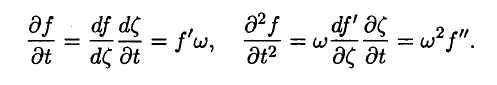
Аналогично

П![]() одстановка
последних двух выражений в волновое
уравнение приводит к выводу, что функция
одстановка
последних двух выражений в волновое
уравнение приводит к выводу, что функция
удовлетворяет волновому уравнению, если положить v = ω/k.
Всякая функция,
удовлетворяющая волновому уравнению,
описывает некоторую волну, причем корень
квадратный из величины, обратной
коэффициенту при
![]() ,
дает фазовую
скорость этой волны.
,
дает фазовую
скорость этой волны.
Для плоской волны, распространяющейся вдоль оси х, волновое уравнение имеет вид
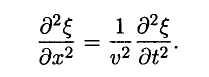
Энергия упругой волны
Пусть в некоторой
среде распространяется в направлении
оси х плоская
продольная волна
![]()
Выделим в среде элементарный объем ΔV, настолько малый, чтобы скорость движения и деформацию во всех точках этого объема можно было считать одинаковыми и равными соответственно дξ/дt и дξ/дх.
Выделенный нами объем обладает кинетической энергией

(ρ ΔV — масса объема, дξ/дt — его скорость).
Рассматриваемый объем обладает также потенциальной энергией упругой деформации
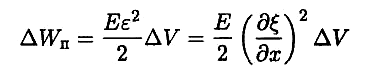
(ε = дξ/дх — относительное удлинение цилиндра, Е — модуль Юнга среды). Заменим модуль Юнга на ρv2 (ρ — плотность среды, v — фазовая скорость волны). Тогда выражение для потенциальной энергии объема ΔV примет вид
Сумма даёт полную
энергию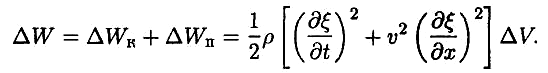
Разделив эту
энергию на объем ΔV,
в котором
она содержится, получим плотность
энергии

Дифференцирование
уравнения
![]() один раз по t,
другой
раз по х дает
один раз по t,
другой
раз по х дает
![]()
Подставив эти выражения в формулу для ω и приняв во внимание, что k2v2 = ω2, получим
![]()
В случае поперечной волны для плотности энергии получается такое же выражение.
Из предыдущего
выражения следует, что плотность энергии
в каждый момент времени в разных
точках пространства различна. В одной
и той же точке плотность энергии
изменяется со временем по закону
квадрата синуса. Среднее значение
квадрата синуса равно 1/2. Соответственно
среднее по времени значение плотности
энергии в каждой точке среды равно
Плотность энергии и ее среднее значение пропорциональны плотности среды ρ, квадрату частоты ω и квадрату амплитуды волны а. Подобная зависимость имеет место не только для незатухающей плоской волны, но и для других видов волн (плоской затухающей, сферической и т. д.).
Итак, среда, в
которой распространяется волна, обладает
дополнительным запасом энергии. Эта
энергия доставляется от источника
колебаний в различные точки среды самой
волной; следовательно, волна переносит
с собой энергию. Количество энергии,
переносимое волной через некоторую
поверхность в единицу времени, называется
потоком энергии через эту поверхность.
Если через данную поверхность переносится
за время dt
энергия
dW,
то поток
энергии Ф равен
![]()
Поток энергии — скалярная величина, размерность которой равна размерности энергии, деленной на размерность времени, т. е. совпадает с размерностью мощности. В соответствии с этим Ф измеряется в ваттах, эргах в секунду и т. п.
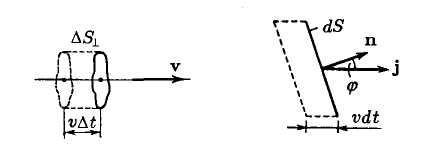
Поток энергии в разных точках среды может быть различной интенсивности. Для характеристики течения энергии в разных точках пространства вводится векторная величина, называемая плотностью потока энергии . Эта величина численно равна потоку энергии через единичную площадку, помещенную в данной точке перпендикулярно к направлению, в котором переносится энергия. Направление вектора плотности потока энергии совпадает с направлением переноса энергии.
Пусть через площадку
![]() ,
перпендикулярную
к направлению распространения волны,
переносится за время Δt
энергия ΔW.
Тогда
плотность потока энергии равна
,
перпендикулярную
к направлению распространения волны,
переносится за время Δt
энергия ΔW.
Тогда
плотность потока энергии равна
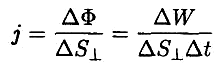
Через площадку
![]() (рис.) будет перенесена за время Δt
энергия ΔW,
заключенная
в объеме цилиндра с основанием
(рис.) будет перенесена за время Δt
энергия ΔW,
заключенная
в объеме цилиндра с основанием
![]() и высотой vΔt
(v
— фазовая
скорость волны). Если размеры цилиндра
достаточно малы (за счет малости
и высотой vΔt
(v
— фазовая
скорость волны). Если размеры цилиндра
достаточно малы (за счет малости
![]() и Δt)
для того,
чтобы плотность энергии во всех точках
цилиндра можно было считать одинаковой,
то ΔW
можно найти как произведение плотности
энергии w
на объем
цилиндра, равный
и Δt)
для того,
чтобы плотность энергии во всех точках
цилиндра можно было считать одинаковой,
то ΔW
можно найти как произведение плотности
энергии w
на объем
цилиндра, равный
![]() vΔt:
vΔt:
![]()
![]() Подставив
это выражение в формулу для j,
получим для плотности потока энергии
Подставив
это выражение в формулу для j,
получим для плотности потока энергии
Наконец, введя вектор v, модуль которого равен фазовой скорости волны, а направление совпадает с направлением распространения волны (и переноса энергии), можно написать
![]()
Мы получили выражение для вектора плотности потока энергии. Этот вектор был введен в рассмотрение Умовым и называется вектором Умова (Пойтинга). Вектор j, как и
плотность энергии Е, различен в разных точках пространства, а в данной точке изменяется со временем по закону квадрата синуса. Его среднее значение равно
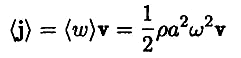
Это выражение, так же справедливо для волны любого вида (сферической, затухающей и т. д.). Отметим, что, когда говорят об интенсивности волны в данной точке, имеют в виду среднее по времени значение плотности потока энергии, переносимой волной.
Зная j во всех точках произвольной поверхности S, можно вычислить поток энергии через эту поверхность. С этой целью разобьем поверхность на элементарные участки dS. За время dt через площадку dS пройдет энергия dW, заключенная в изображенном на рис. косом цилиндре. Объем этого цилиндра равен dV = vdt dS cos φ. В нем содержится энергия dW = w dV = wv dt dS cos φ (w — мгновенное значение плотности энергии в том месте, где расположена площадка dS). Приняв во внимание, что
![]()
(dS
= ndS;
см.рис.),
можно написать dW
= jdSdt.
Отсюда для
потока энергии dФ
через площадку
dS
получается
формула
![]()
Полный поток энергии через поверхность равен сумме элементарных потоков:
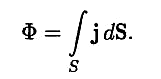 Поток
энергии равен потоку вектора j
через поверхность S.
Поток
энергии равен потоку вектора j
через поверхность S.
Заменив вектор j его средним по времени значением, получим среднее значение Ф:
![]()
Вычислим среднее
значение потока энергии через произвольную
волновую поверхность незатухающей
сферической волны. В каждой точке
этой поверхности векторы j
и dS
совпадают
по направлению. Кроме того, модуль
вектора j
для всех точек поверхности одинаков.
Следовательно,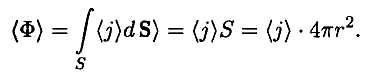
(r — радиус волновой поверхности). ‹ j › = ρa2ω2v/2. Таким образом,
![]() (аr
— амплитуда
волны на расстоянии r
от источника).
(аr
— амплитуда
волны на расстоянии r
от источника).
Звук — колебательное движение частиц упругой среды, распространяющееся в виде волн в газообразной, жидкой или твёрдой средах. Человек слышит З. с частотой от 16 гц до 20 000 гц. Физическое понятие о З. охватывает как слышимые, так и неслышимые звуки. З. с частотой ниже 16 гц называется инфразвуком, выше 20 000 гц — ультразвуком; самые высокочастотные упругие волны в диапазоне от 109 до 1012—1013 гц относят к гиперзвуку. Область инфразвуковых частот снизу практически не ограничена — в природе встречаются инфразвуковые колебания с частотой в десятые и сотые доли гц. Частотный диапазон гиперзвуковых волн сверху ограничивается физическими факторами, характеризующими атомное и молекулярное строение среды: длина упругой волны должна быть значительно больше длины свободного пробега молекул в газах и больше межатомных расстоянии в жидкостях и в твёрдых телах. Поэтому в воздухе не может распространяться гиперзвук с частотой 109 гц и выше, а в твёрдых телах — с частотой более 1012—1013 гц.
Основные характеристики звука. Важной характеристикой З. является его спектр, получаемый в результате разложения З. на простые гармонические колебания (т. н. частотный звука анализ). Спектр бывает сплошной, когда энергия звуковых колебаний непрерывно распределена в более или менее широкой области частот, и линейчатый, когда имеется совокупность дискретных (прерывных) частотных составляющих. З. со сплошным спектром воспринимается как шум, например шелест деревьев под ветром, звуки работающих механизмов. Линейчатым спектром с кратными частотами обладают музыкальные З.; основная частота определяет при этом воспринимаемую на слух высоту звука, а набор гармонических составляющих — тембр звука. В спектре З. речи имеются форманты — устойчивые группы частотных составляющих, соответствующие определённым фонетическим элементам. Энергетической характеристикой звуковых колебаний является интенсивность звука — энергия, переносимая звуковой волной через единицу поверхности, перпендикулярную направлению распространения волны, в единицу времени. Интенсивность З. зависит от амплитуды звукового давления, а также от свойств самой среды и от формы волны. Субъективной характеристикой З., связанной с его интенсивностью, является громкость звука, зависящая от частоты. Наибольшей чувствительностью человеческое ухо обладает в области частот 1—5 кгц. В этой области порог слышимости, т. е. интенсивность самых слабых слышимых звуков, по порядку величины равна 10-12вт/м2, а соответствующее звуковое давление — 10-5н/м2. Верхняя по интенсивности граница области воспринимаемых человеческим ухом З. характеризуется порогом болевого ощущения, слабо зависящим от частоты в слышимом диапазоне и равным примерно 1 вт/м2. В ультразвуковой технике достигаются значительно большие интенсивности (до 104 квт/м2).
Уровень громкости
в децибелах (дБ):
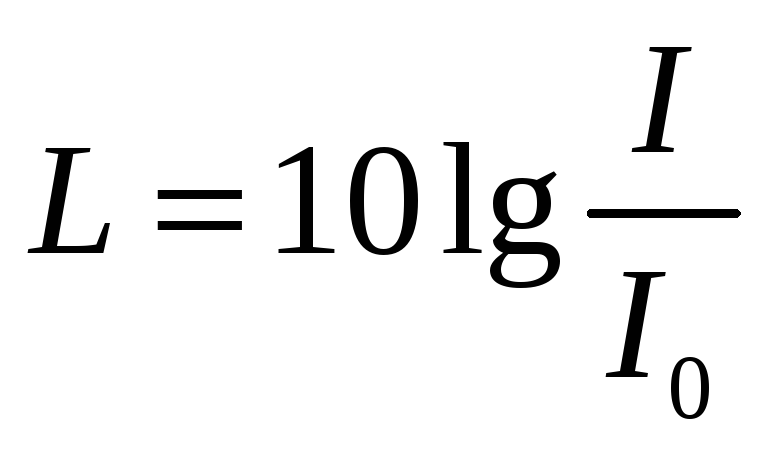 ,
где I0
– исходная интенсивность (принимается
равной 10-12
Вт/м2)
,
где I0
– исходная интенсивность (принимается
равной 10-12
Вт/м2)
Звуковая волна в газе представляет собой распространяющуюся в пространстве последовательность чередующихся областей сжатия и разряжения газа.
Скорость звука в
газе (выведена при учёте, что процесс
распространения в пространстве
последовательность чередующихся
областей сжатия и разряжения газа
адиабатический):
 ,
М – масса одного моля.
,
М – масса одного моля.
Средняя скорость
теплового движения молекул газа:
![]() .
.
Интерференция и дифракция упругих волн – сущность явления и способы практического осуществления.
И нтерференция.
При приходе в данную точку среды двух
волн их действие складывается. Особо
важное значение имеет наложение так
называемых когерентных волн (т. е. волн,
разность фаз которых постоянна, не
меняется со временем). В случае
когерентности волн имеет место явление,
называемое интерференцией: в точках,
куда обе волны приходят в фазе, они
усиливают друг друга; в точках же, куда
они попадают в противофазе, — ослабляют
друг друга. В результате получается
характерная интерференционная картина.
Стоячие волны – волны, возникающие
вследствие интерференции волн,
распространяющихся во взаимно
противоположных направлениях. Практически
С. в. возникают при отражениях волн от
преград и неоднородностей в результате
наложения отражённой волны на прямую.
нтерференция.
При приходе в данную точку среды двух
волн их действие складывается. Особо
важное значение имеет наложение так
называемых когерентных волн (т. е. волн,
разность фаз которых постоянна, не
меняется со временем). В случае
когерентности волн имеет место явление,
называемое интерференцией: в точках,
куда обе волны приходят в фазе, они
усиливают друг друга; в точках же, куда
они попадают в противофазе, — ослабляют
друг друга. В результате получается
характерная интерференционная картина.
Стоячие волны – волны, возникающие
вследствие интерференции волн,
распространяющихся во взаимно
противоположных направлениях. Практически
С. в. возникают при отражениях волн от
преград и неоднородностей в результате
наложения отражённой волны на прямую.
Падающая волна:
![]() ,
отраженная:
,
отраженная:
![]() .
.
складываем:
![]() –
–
уравнение стоячей волны.
Выбираем начало
отсчета x
и t
так, чтобы выполнялось:
![]()
![]()
Координаты узлов
(min):
![]()
К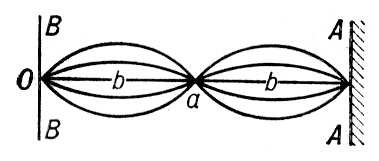 оординаты
пучностей (max):
оординаты
пучностей (max):
![]()
Рис. Стоячая волна, возникшая в результате интерференции падающей и отраженной от препятствия АА волны; в точке а — узел колебания, в точках b — пучности.

Д
Рис. Образование
тени при падении волны: а — на непрозрачное
тело; б — на отверстие в непрозрачном
экране (d — paзмер тела или отверстия).
 Дифракция имеет
место также при прохождении волны через
отверстие (рис.),
где она также выражается в проникновении
волны в область тени и в некотором
изменении характера волны в «освещённой»
области: чем меньше диаметр отверстия
по сравнению с длиной волны, тем шире
область, в которую проникает волна.
Дифракция имеет
место также при прохождении волны через
отверстие (рис.),
где она также выражается в проникновении
волны в область тени и в некотором
изменении характера волны в «освещённой»
области: чем меньше диаметр отверстия
по сравнению с длиной волны, тем шире
область, в которую проникает волна.
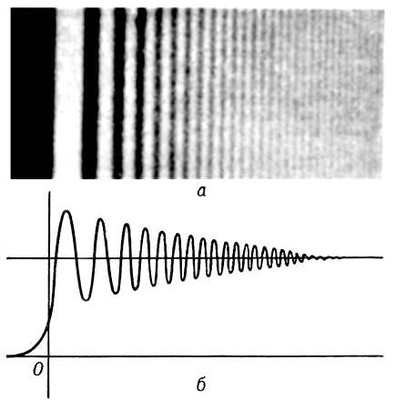
Р ис.
а — дифракция света от края экрана;
виден сложный переход от света к тени;
б — кривая, характеризующая освещенность
пространства между светом и тенью; край
экрана в точке О.
ис.
а — дифракция света от края экрана;
виден сложный переход от света к тени;
б — кривая, характеризующая освещенность
пространства между светом и тенью; край
экрана в точке О.
