ГОС / 17

17.Постоянный ток в металлах. Закон Ома. Правила Кирхгофа. Мощность постоянного тока, закон Джоуля. Понятие о сверхпроводимости.

Закон Ома - это экспериментальный закон и в дифференциальной форме он имеет следующий вид:

(2.1), где

– напряженность электрического поля,

– плотность тока,

– удельная проводимость.

(, где ρ – удельное сопротивление)

Из закона Ома следует, что плотность тока пропорциональна напряженности электрического поля.

, где ρ – плотность заряда (ρ(t)=Const) (2.2)

Для постоянных токов плотность не зависит от времени, тогда (2.3)

Это уравнение говорит о том, что линии постоянного тока не могут обрываться, они либо замкнуты, либо уходят на бесконечность.

П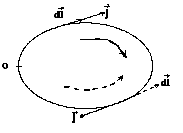осчитаем циркуляцию вектора плотности тока вдоль замкнутого контура. Замкнутый контур выберем совпадающим с токовой линией.

Вектор может быть направлен по вектору плотности тока или противоположно ему. В первом случае скалярное произведение и будет положительным, во втором отрицательным.

Т. е. циркуляция вектора плотности постоянного тока вдоль замкнутого контура равна нулю. Это говорит о том, что постоянный ток при наличии только электростатических сил невозможен.

Постоянный электрический ток при прохождении по проводнику выделяет тепло (джоулево тепло). При циркуляции постоянного электрического тока по замкнутому контуру работа электростатических сил равна нулю. Следовательно, для поддержания постоянного тока необходим источник, который являлся бы сторонним по отношению к электростатическому полю и все время пополнял энергию магнитного поля, выделяющуюся в виде тепла.

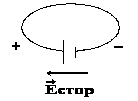
(2.5) (2.6)

(2.6) – обобщенный закон Ома в дифференциальной форме.

Закон Ома для линейных проводников.

П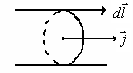од линейным проводником будем понимать такой проводник, в котором в поперечном сечении вектор плотности тока не меняется и совпадает с направлением касательной к проводнику.

Рассмотрим линейный проводник, по которому течет постоянный ток.

Умножим (2.6) на элемент длины и проинтегрируем по всей длине проводника:

: (2.7) (2.7’)

1). (2.8)

, , - сопротивление проводника

- сопротивление всего рассматриваемого проводника

2). (2.9) – разность потенциалов на концах проводника

3). (2.10) – работа при перемещении единичного заряда из 1 в 2. А по определению это есть ЭДС сторонних сил.

Подставляя (2.8 – 2.10) в (2.7’), получим: (2.11)

(2.11) – закон Ома в интегральной форме для участка цепи или для незамкнутого проводника: падение напряжения на участке цепи равно разности потенциалов на этом участке + ЭДС сторонних сил.

Если участок цепи или проводник замкнутый, то . Тогда

(2.12)

(2.12) – закон Ома в интегральной форме для замкнутого проводника: падение напряжения замкнутого проводника равно ЭДС сторонних сил.

В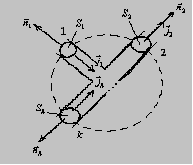ыражение (2.12) говорит о том, что существование и сила постоянных токов действительно обуславливается наличием сторонних электродвижущих сил.

Правила Кирхгофа.

Рассмотрим линейные проводники. Пусть k – проводников сходятся в одну точку. Точка, в которой сходятся три и более проводников, называется узлом. В каждом проводнике ток может течь по-разному. Нормаль выбирается выходящей из поверхности. Окружим данные проводники поверхностью произвольного объема.

(3.1) – закон сохранения заряда в дифференциальной форме.

Проинтегрируем по объему , получим (3.2).

По теореме Остроградского-Гаусса перейдем к интегралу по поверх: (3.3)

Выбранная нами поверхность будет складываться из площадей поперечного сечения каждого проводника, через которые проходят токи, и поверхностей, где токов нет. Поэтому данный интеграл разобьется на k – интегралов, где токов нет, по площадям S₁, S₂,…, S_k:

(3.4)

По определению каждый из этих интегралов равен току, протекающему в данном проводнике:

(3.5). Тогда (3.6).

Плотности токов могут быть направлены по-разному, и токи текут в разных направлениях. Следовательно, алгебраическая сумма токов, сходящихся в узле, равна нулю. Это I правило Кирхгофа.

Если ток втекает в узел, то его считают положительным; если вытекает – отрицательным.

Рассмотрим замкнутый контур. В этом контуре выделим участок цепи ik . Для данного участка цепи мы можем записать закон Ома в интегральной форме:

Просуммируем для всего замкнутого контура:

(3.7) – алгебраическая сумма падений напряжений во всем контуре равна алгебраической сумме ЭДС. Это II правило Кирхгофа.

При записании II правила Кирхгофа выбираем обход контура. Если направление выбранного нами тока совпадает с направлением обхода, то ток со знаком «+», если противоположно, то «-». Если направление ЭДС совпадает на участке с обходом контура, то оно выбирается со знаком «+», если противоположно, то «-».

При протекании постоянного тока по проводникам происходит их нагревание. Электрический ток сродни течению жидкости. Для того чтобы жидкость двигалась по трубам, необходимо работа по преодолению вязких сил. Аналогично и для протекания постоянного тока по проводам необходим источник сторонних по отношению к электростатическому полю, который пополнял бы энергию магнитного поля, выделяясь в виде джоулева тепла.

Вычислим количество теплоты, выделяемое в проводнике при прохождении

по нему постоянного электрического тока.

(4.1) – плотность силы Лоренца

(4.2)

Получили мощность, выделяемую токами в виде джоулева тепла. Если умножить эту величину на элемент объема, то получим мощность в элементе объема:

(4.3)

Величина называется плотностью тока (4.3’)

С другой стороны, из закона Ома в дифференциальной форме:

Тогда с учетом сказанного (4.4)

Перейдем к линейным токам. Рассмотрим элемент объема линейного тока. Пусть площадь поперечного сечения S.

(4.5)

Для линейных проводников можно переходить от объемного элемента с током к линейному по формуле (4.5). При этом объемный интеграл переходит в линейный и если проводник замкнут, то линейный интеграл замкнут, и наоборот. Подставив (4.5) в (4.3’) получим

(4.6)

(4.6) количество теплоты, выделившееся линейным проводником в единицу времени.

Если проводник замкнут, то , а следовательно (4.7)

Выражение (4.7) говорит о том, что все тепло, выделяемое в замкнутом контуре, обусловлено мощностью сторонних сил.

Запишем закон Ома в интегральной форме для замкнутого контура:

(4.8) (4.9)

(4.9) – закон Джоуля – Ленца и он говорит о том, что количество теплоты, выделяемое в замкнутом контуре прямо пропорционально квадрату силы тока, сопротивлению и времени.

Понятие о сверхпроводимости.

В 1911 году голландский ученый Камерлит обнаружил, что сопротивление некоторых веществ при сверхнизких температурах (порядка 4 К) резко падает до нуля. Никакими сверхточными приборами невозможно было обнаружить сопротивление. Это явление было названо сверхпроводимостью.

Д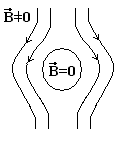о середины 50-х годов природа данного явления была непонятна, но при этом были проведены многочисленные эксперименты, которые показали, что магнитное поле огибает сверхпроводник.

Температура сверхпроводникового перехода зависит от массы ядер вещества.

«Плохие» проводники, например олово и свинец, являются хорошими сверхпроводниками.

Природу сверхпроводимости объяснили в своей теории Бардин, Купер и Шриффер. Природу сверхпроводимости смогла объяснить только квантовая теория. Суть ее в следующем: электроны в проводнике взаимодействуют с колебаниями решетки, (колебания решетки отождествляют с частицами фотонами). При этом образуются пары частиц с противоположными спинами. Такие пары были названы куперовскими. Куперовские пары имеют общий спин, равный нулю, относятся к бозе-частицам и обладают способностью перемещаться в сверхпроводнике без трения и без выделения тепла. При этом если создать поток таких куперовских пар, то возникший электрический ток будет существовать практически вечно.