ГОС / 8

Вопрос 8. Принцип наименьшего действия. Уравнения Лагранжа. Канонические уравнения Гамильтона.

Обобщенные координаты

Связь – это ограничение движения тела. ( Ограничения: например- тело находится на плоскости z=h).

Определение: Если ограничения накладываемые связями могут быть выражены в виде равенства, связывающего координаты частиц и время, т.е. f(₁, _2, …_n, t)=0 то такие связи называются голономными.

Связи вносят в решение механических задач трудности, т.к. не все переменные в уравнениях Ньютона оказываются независимыми, кроме того возникают реакции связи.

Трудности, накладываемые голономными связями можно разрешить, если ввести обобщенные координаты. Для определения положения системы из N материальных точек в пространстве надо задать N радиус-векторов, т.е. 3N координат. Если на систему наложены голономные связи, выражаемые k уравнениям, то мы можем с их помощью исключить k координат из общего числа и получить таким образом 3N-k независимых координат. Число независимых величин, задание которых необходимо для однозначного определения положения системы наз. числом ее степеней свободы, в дан. случае их S=3N-k. Исключение зависимых координат может быть произведено и другим путем. Он состоит в том, что вводят S независимых координат q₁, q_2, q_3, ….., q_s, характеризующих положение системы ( с S степенями свободы). Такие координаты называются обобщенными координатами,

Пр. Тело движется на плоскости – 2 степени свободы, значит q₁=x, q₂=y.

Обобщенные координаты могут быть любыми, но требования к ним следующие:

1. чтобы их количество должно = количеству степеней свободы

2. задание обобщенных координат полностью описывало положение точки.

Пр.:-обобщенная координата при движении математического маятника.

Производные обобщенных координат по времени ₁, ₂, …., _s наз. обобщенными скоростями.

В дальнейшем для краткости мы будем чисто условно будем понимать под q совокупность всех координат q₁, q_2, q_3, ….., q_s и под аналогично совокупность всех ее скоростей ₁, ₂, …., _s.

Принцип наименьшего действия

Одновременное задание всех координат и скоростей в классической механике полностью определяет, как показывает опыт, состояние системы и позволяет в принципе предсказать дальнейшее ее движение . С математической точки зрения это значит, что заданием всех координат обобщенных q и обобщенных скоростей в некоторый момент времени однозначно определяется также и значение ускорений в этот момент. Соотношения, связывающие ускорения с координатами и скоростями, называются уравнениями движения. По отношению к функциям это дифференциальные уравнения второго порядка, интегрирование которых позволяет в принципе определить эти функции, т.е. траектории движения механических систем.

Наиболее общая формулировка закона движения механических систем дается так называемым принципом наименьшего действия (или принципом Гамильтона). Согласно этому принципу, каждая механическая система характеризуется определенной функцией

L(q₁, q_2, q_3, ….., q_{s, 1}, ₂, …., _n, t).

Или, к краткой записи, , Функция определяет состояние системы в целом и называется функцией Лагранжа. Движение системы удовлетворяет следующему условию.

Пусть в моменты времени и система занимает определенные положения, характеризуемые двумя наборами значений координат и . Тогда между этими положениями система движется таким образом, что интеграл

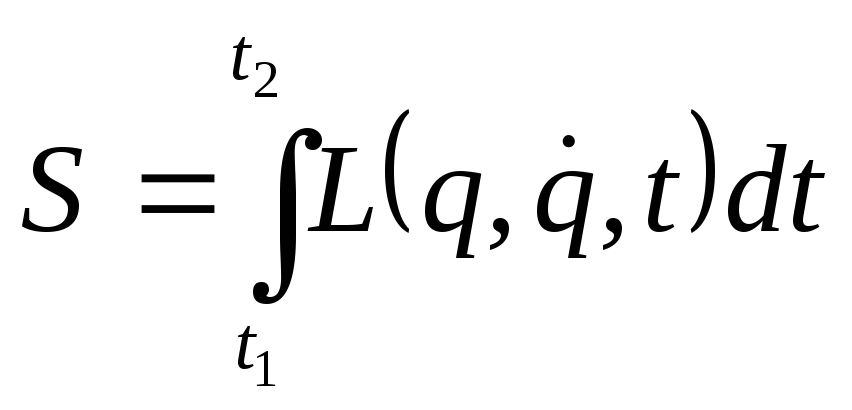
имел наименьшее возможное значение. Величина S называется действием. Тот факт, что функция Лагранжа содержит только q и , но не более высокие производные и т.д., является выражением указанного ранее факта, что механическое состояние полностью определяется заданием координат и скоростей. Действие является функционалом. Для нахождения минимума функционала, нужно взять вариацию функционала и приравнять к нулю. Таким образом, принцип наименьшего действия можно записать в виде

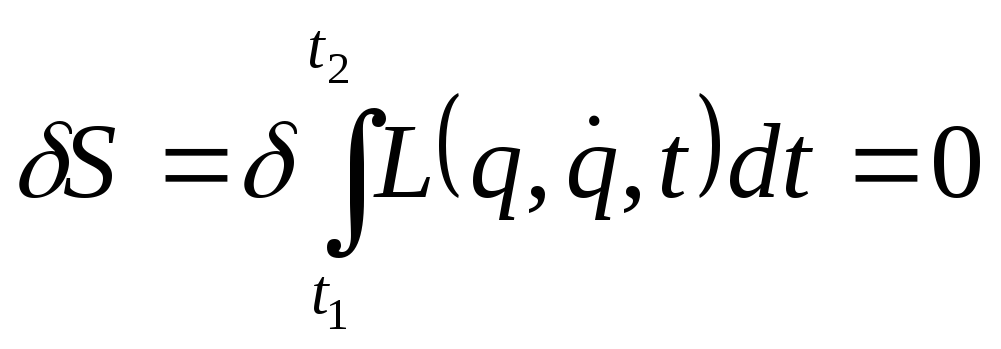
Произведя варьирование, можно получить уравнение Лагранжа

-уравнение Лагранжа

При наличии нескольких степеней свободы в принципе наименьшего действия должны независимо варьироваться s неизвестных функций . Очевидно, мы получим систему из s уравнений

Функция Лагранжа системы материальных точек.

L=- U (q₁, q_2, q_3, ….., q_s, t)

U (q₁, q_2, q_3, ….., q_s, t)- потенциальная энергия.

=T-кинетическая энергия.

Зная функцию Лагранжа, можно получить уравнение движения.

Пример 1. Точка движется в декартовой системе координат. Система имеет 3 степени свободы, достаточно 3 координат- x, y, z. .Составим функцию Лагранжа:

T=, U=U(x, y, z).

Система уравнений Лагранжа -

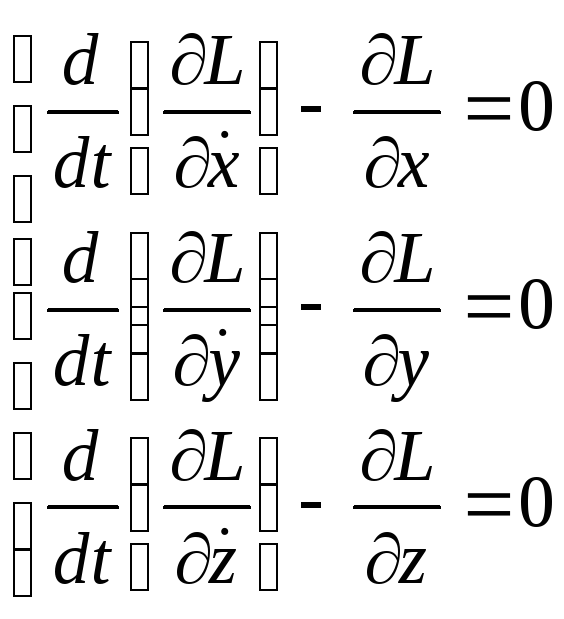
Известно, что для потенциальных сил

При подстановке вычисленных производных в систему уравнений Лагранжа, получим

F_x

F_y - 2 з-н Ньютона.

F_z

В теоретической механике существует понятие -=Q_i, которая наз. обобщенной силой.

Пример 2. Точка движется в полярной системе координат на плоскости. Система имеет 2 степени свободы, достаточно 2 координат- r и . .Составим функцию Лагранжа:

Вычислим скорость

T=, U=U( r, ).

Система уравнений Лагранжа -

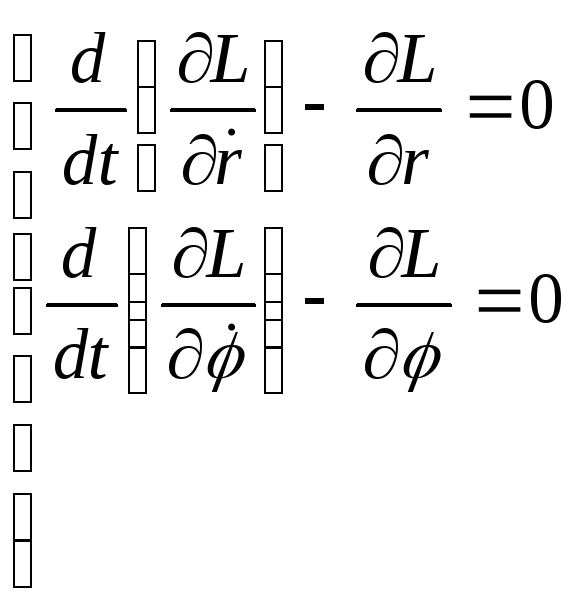
Где -проекция силы на радиальную ось, -модуль центробежной силы,-проекция момента силы на z.

При подстановке вычисленных производных в систему уравнений Лагранжа, получим

то есть - основное уравнение вращательного движения - момент инерции, проекция ускорения на ось z

П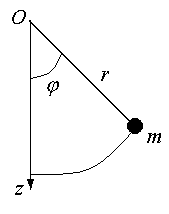ример 3. Покажем метод решения задач по механике с помощью уравнения Лагранжа. В качестве обобщенной координаты примем угол отклонения маятника от положения равновесия ..Составим функцию Лагранжа:

Воспользуемся формулой скорости в полярной системе координат. Учтем, что точка движется по окружности с радиусом, равным длине нити.

T=, U=.

Уравнений Лагранжа -

Вычисляем призводные

При подстановке вычисленных в систему уравнений Лагранжа, получим

То есть получили широко известное уравнение математического маятника

Преимущества вариационной концепции.

1. 2 закон Ньютона был выведен из опыта. Эксперимент может давать погрешности, поэтому теоретический вывод 2-ого закона Ньютона был необходимым, он более строгий.

2. Количество уравнений Лагранжа меньше, чем система уравнений Ньютона.

3. В уравнениях Лагранжа не нужно учитывать связи.

4. Уравнения Лагранжа являются более общими.

Определение: Под обобщенным импульсом или обобщенным количеством движения понимают величину P_i=, L- функция Лагранжа, - обобщенная координата. Каждой координате соответствует свой обобщенный импульс.

Пример. Если - декартовая координата x.

L=- U(x)

= =P_x проекция обычного импульса на ось z

Канонические уравнения Гамильтона.

Формулирование законов механики с помощью функции Лагранжа предполагает описание механического описания системы путем задания ее обобщенных координат и скоростей. Такое описание не является единственно возможным. В подходе Гамильтона задание положения системы осуществляется с помощью обобщенных координат и обобщенных импульсов.

Вводится функция Гамильтона по формуле

или - Функция Гамильтона или гамильтониан

Физический смысл гамильтониана в классической механике – полная энергия системы, то есть

Уравнения движения в переменных p и q

и - канонические уравнения Гамильтона.

Они составляют систему 2s дифференциальных уравнений первого порядка для 2s неизвестных функций и , заменяющих собой s уравнений второго порядка лагранжевого метода.