
ГОС / 39
.doc39. Уравнение Шредингера. Классическая механика как предельный случай квантовой. Принцип причинности в квантовой механике. Стационарное уравнение Шредингера и свойства стационарных состояний. Связь энергетического спектра с видом потенциала.
Квантовомеханический
принцип причинности утверждает, что
если известна волновая функция системы
в начальный момент времени
![]() ,
то с помощью волнового уравнения
(уравнение Шредингера) можно получить
волновую функцию в последующий момент
времени
,
то с помощью волнового уравнения
(уравнение Шредингера) можно получить
волновую функцию в последующий момент
времени
![]() (t>0).
(t>0).
Из
принципа причинности следует, что в
квантовой механике нет понятия траектории,
а
![]() определяется только в последующий
момент времени. Зная волновую функцию,
можем определить среднее значение
физических величин.
определяется только в последующий
момент времени. Зная волновую функцию,
можем определить среднее значение
физических величин.
Согласно принципу причинности в квантовой механике знание волновой функции в начальный момент времени должно определять состояние системы в последующий момент времени.
t=0:
![]() t>0:
t>0:
![]()
Определим
![]() через промежуток
времени
через промежуток
времени
![]() ,
то есть в момент t>0(
,
то есть в момент t>0(![]() 0).
0).
![]()
![]() 2.1.
2.1.
Уравнение 2.1. показывает, что знание волновой функции в момент t=0 должно определять и ее первую производную в момент t=0. То есть между самой функцией при t=0 и ее первой производной должно быть установлено некоторое соотношение. Это соотношение должно быть операторным:
![]() 2.2.
2.2.
2.2.
определяет соотношение между волновой
функцией в момент времени t=0
и ее первой производной в этот же момент
времени. Это соотношение дается через
оператор, то есть является операторным.
Оператор
![]() реализует принцип причинности. Оператор
реализует принцип причинности. Оператор
![]() не может содержать первых, вторых и
высших производных по времени. Первая
производная по времени находится в
левой части.
не может содержать первых, вторых и
высших производных по времени. Первая
производная по времени находится в
левой части.
Если же оператор будет содержать вторые и высшие производные, то при определении волновой функции в момент времени t необходимо в момент времени t=0 задавать не только саму волновую функцию, но и ее производную, что противоречит принципу причинности.
2.2. мы записали для момента времени t=0, при этом момент времени выбирался произвольно. Следовательно, 2.2. мы записали для любого момента времени.
![]() 2.2'.
2.2'.
Рассмотрим свободную частицу:
![]()
![]()
![]() 2.3.
2.3.
2.3.
говорит о том, что в качестве оператора
![]() c
точностью до множителя мы можем взять
оператор полной энергии
c
точностью до множителя мы можем взять
оператор полной энергии
![]() .
.
Тогда:
![]() 2.4.
2.4.
2.4.- уравнение Шредингера для произвольных состояний, зависящих от времени.
![]() 2.4'.
2.4'.
Волна де Бройля описывается свободной частицей.
![]() →
→![]()
![]()
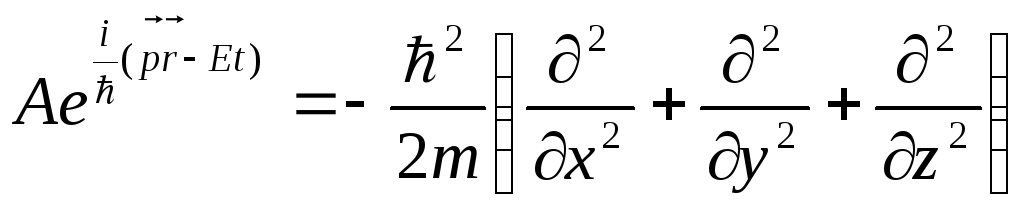
![]()
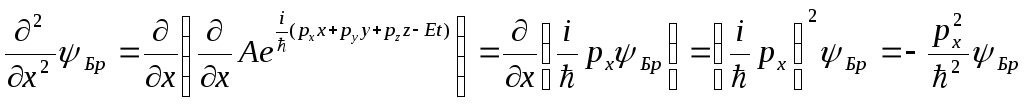
![]()
Приведенные результаты не доказывают, а показывают справедливость уравнения 2.4. или 2.4'. Данное уравнение в квантовой механике играет такую же роль, как законы Ньютона в классической механике. Оно не доказывается, а его справедливость следует из опыта. Наиболее употребимо уравнение Шредингера 2.4'.
![]() 2.5.
2.5.
Состояние, не зависящее от времени, называется стационарным.
Запишем уравнение Шредингера для произвольных состояний:
![]() (4.1)
(4.1)
![]() (4.2)
(4.2)
Если
![]() является
только функцией координат и не зависит
от времени, то
является
только функцией координат и не зависит
от времени, то
![]() так
же от времени не зависит.
так
же от времени не зависит.
Тогда
уравнение Шредингера можно решать
методом разделения переменных, т. е.
волновую функцию
![]() можно представить:
можно представить:
![]() (4.3)
(4.3)
![]() (4.4)
(4.4)
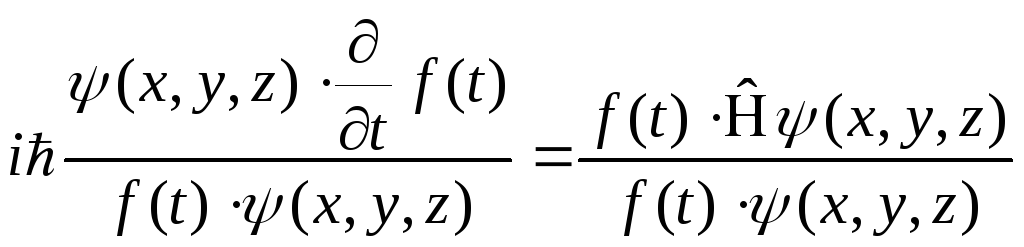 (4.4')
(4.4')
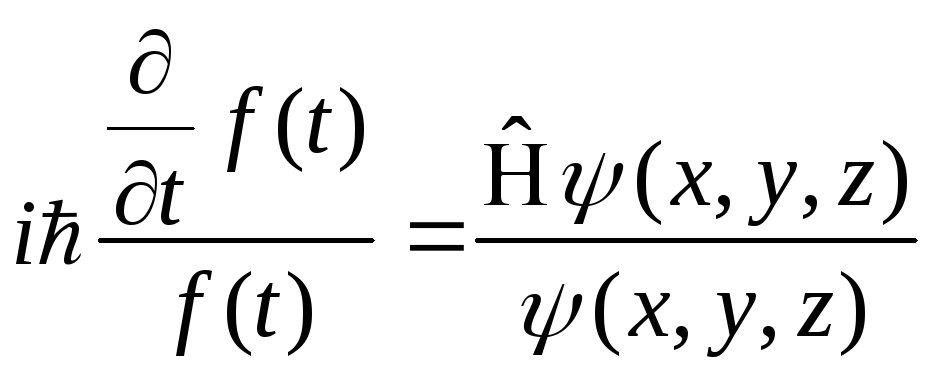 (4.5)
(4.5)
Левая часть зависит только от времени, правая часть зависит только от координат. Эти части равны какой-то постоянной величине.
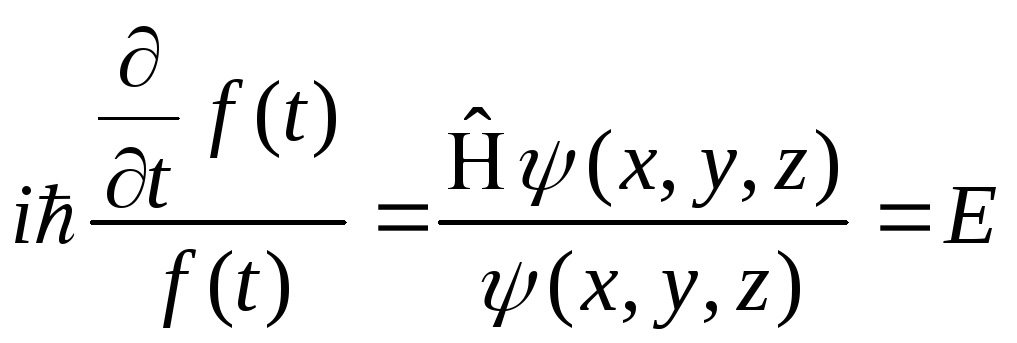 (4.5')
(4.5')
![]() (4.6)
(4.6)
(4.6)
представляет собой уравнение на
собственные функции и собственные
значения оператора
![]() .
.
Т.
к.
![]() оператор
полной энергии, то
оператор
полной энергии, то
![]() -
собственные значения этого оператора.
И это есть те значения полной энергии,
которые определяются из эксперимента.
-
собственные значения этого оператора.
И это есть те значения полной энергии,
которые определяются из эксперимента.
![]() -
собственные функции оператора полной
энергии.
-
собственные функции оператора полной
энергии.
Физически уравнение (4.6) называется уравнением Шредингера для стационарных состояний.
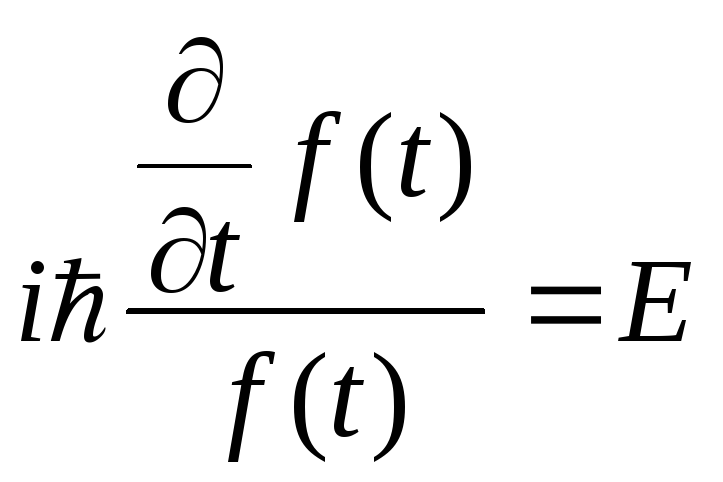 (4.7)
(4.7)
![]()
![]()
![]() (4.8)
(4.8)
![]() (4.9)
(4.9)
Волновая функция (4.9) является решением стационарного уравнения Шредингера. Стационарность состоит в том, что ни плотность вероятности, ни вектор плотности тока вероятности, ни условие нормировки не зависят от времени.
![]() (4.10)
(4.10)
– плотность вероятности не зависит от времени.
Вектор плотности тока вероятности не зависит от времени:
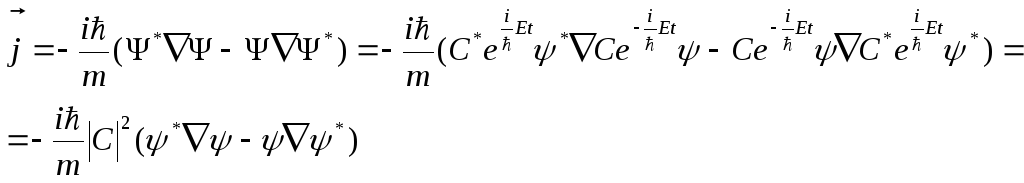 (4.11)
(4.11)
Условие нормировки так же не зависит от времени:
![]()
![]() (4.12)
(4.12)
То,
что волновая функция (4.9) есть волновая
функция стационарного состояния
(является решением стационарного
уравнения Шредингера) при решении
стационарных задач позволяет «забывать»
о временной зависимости. В необходимых
случаях (квантовые переходы) волновая
функция легко восстанавливается
умножением на функцию
![]() (4.8).
(4.8).
![]() (5.1)
(5.1)
![]() (5.2)
(5.2)
![]() (5.3)
(5.3)
![]() (5.4)
(5.4)
Уравнение (5.4) на собственные функции и собственные значения оператора полной энергии.
Волновая
функция
![]() должна
быть однозначной, т.е. однозначно
определяться из данного уравнения.
Также она должна быть непрерывной
функцией координат.
должна
быть однозначной, т.е. однозначно
определяться из данного уравнения.
Также она должна быть непрерывной
функцией координат.
Если потенциальная энергия не испытывает бесконечных скачков в какой-либо области пространства, то непрерывными должны быть и первые производные волновой функции.
Выясним, при каких условиях уравнение Шредингера имеет непрерывный спектр собственных значений, при каких - дискретный спектр и когда физических решений вообще нет.
Решить стационарное уравнение Шредингера – это значит найти собственные значения оператора полной энергии.
Рассмотрим первый случай.
Предположим, что на бесконечности потенциальная энергия обращается в ноль.
![]()
Тогда
![]() (5.5)
(5.5)
Решение
![]() (5.6)
(5.6)
координатная часть волны де Бройля.
![]()
![]() >0
– кинетическая энергия свободной
частицы.
>0
– кинетическая энергия свободной
частицы.
Частицы,
обладающие
![]() >0,
могут уходить на бесконечность, т.е.
движение таких частиц является инфинитным,
или неограниченным.
>0,
могут уходить на бесконечность, т.е.
движение таких частиц является инфинитным,
или неограниченным.
Рассмотрим второй случай.
Потенциальная
энергия
![]() >0,
полная энергия
>0,
полная энергия
![]() <0.
<0.
Т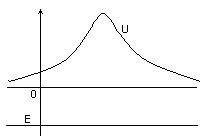 огда
огда
![]() (5.7)
(5.7)
Решение в виде волны де Бройля не существует.
Покажем это:
![]()
![]() (5.7')
(5.7')
![]() >0
>0 ![]() <0
<0
Левая часть уравнения положительная, правая часть отрицательная. Следовательно, решения в виде волны де Бройля не существует.
Математически решение уравнения Шредингера (5.7) есть. В одномерном случае это суперпозиция двух решений:
![]() .
.
Однако
физически данное решение является
бессмысленным. Действительно, при
![]() ,
,
![]() .
А значит, плотность вероятности
.
А значит, плотность вероятности
![]() .
.
Т.е. вероятность обнаружить частицу в единице любого объема пространства бесконечно, что физически бессмысленно. Поэтому состояния с отрицательной энергией при положительной потенциальной энергии не существует.
Рассмотрим третий случай.
Пусть
потенциальная энергия меньше нуля
![]() <0,
полная энергия меньше нуля
<0,
полная энергия меньше нуля
![]() <0,
но
<0,
но
![]() >
>![]() .
И пусть
.
И пусть
![]() .
.
Уравнение
запишем в виде:
![]() (5.8)
(5.8)
Н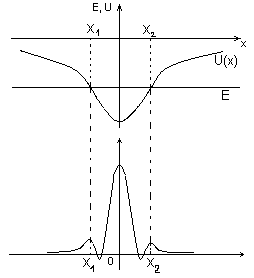 а
данном отрезке решением уравнения будет
волна де Бройля. Вне этого отрезка
координатная волновая функция будет
экспоненциально затухать. Данная
волновая функция говорит о том, что
частица, описываемая этой волновой
функцией, локализована в некоторой
потенциальной яме, причем на бесконечности
волновая функция стремится к нолю.
а
данном отрезке решением уравнения будет
волна де Бройля. Вне этого отрезка
координатная волновая функция будет
экспоненциально затухать. Данная
волновая функция говорит о том, что
частица, описываемая этой волновой
функцией, локализована в некоторой
потенциальной яме, причем на бесконечности
волновая функция стремится к нолю.
Состояние, при котором частицы находятся в некоторой ограниченной области, называется финитным или ограниченным.
В
точках
![]() и
и
![]() полная энергия равна потенциальной
энергии. В классической механике эти
точки называются точками поворота.
полная энергия равна потенциальной
энергии. В классической механике эти
точки называются точками поворота.
Частицы за точками поворота оказаться не могут, т.е. в классической механике частицы, находящиеся внутри потенциальной ямы, выйти из нее не могут. В квантовой механике состояние микрочастиц описывается волновой функцией. Видим, что за точками поворота волновая функция хоть и мала, но все же отлична от нуля. Т.е. вероятность обнаружить частицу с энергией меньше потенциальной энергии хоть и мала, но отлична от нуля (радиоактивный распад).
Решение в области энергий Е < Umin отсутствует, при Umin < E < U(±∞) решение существует лишь при некоторых дискретных E. В области E > U(±∞)решение существует для любых E (непрерывный спектр).
