ГОС / 04

4. Закон сохранения механической энергии и его связь с однородностью времени. Работа силы. Понятие консервативных и неконсервативных сил. Потенциальные силовые поля. Кинетическая и потенциальная энергии.

Уравнение движения материальной точки массы m, движущейся под действием сил, результирующая которых равна : . (Второй закон Ньютона)

Умножим скалярно правую и левую часть этого равенства на элементарное перемещение точки , тогда (1)

Так как , то _. (Здесь V – модуль скорости) Используя последнее равенство и то обстоятельство, что масса материальной точки постоянная величина, преобразуем (1) к виду.

Проинтегрировав части этого равенства вдоль траектории частицы от точки 1 до точки 2, имеем: (3)

Работа силы

Если сила перемещает тело на некоторое расстояние, то она совершает над телом работу. Работа есть интеграл от силы по перемещению. То есть

Единицей работы в СИ служит работа, совершаемая на пути в один метр с силой в один ньютон, действующей в направлении перемещения. Эта единица называется джоулем (Дж), т.е. 1 Дж = 1 Н 1 м. Все силы, встречающиеся в механике, принято разделять на консервативные и неконсервативные. Если силовое поле таково, что работа силы на любом замкнутом контуре, равна нулю, то есть , (4) то такая сила (система) называется консервативной. Примеры консервативных сил – сила тяжести, сила упругости. С физической точки зрения ясно, что при наличии трения или других диссипативных сил система не может быть консервативной, ток как соответствующей этой силе член будет все время отрицательным, и поэтому интеграл (4) не может обратиться в нуль. Согласно теореме Стокса (векторный анализ) условие консервативности сил можно записать в виде . Такие силы также называются потенциальными. Так как всегда равен нулю, то консервативную силу можно представить в виде в виде градиента некоторого скаляра, то есть

Величина называется потенциальной энергией. Для консервативных сил

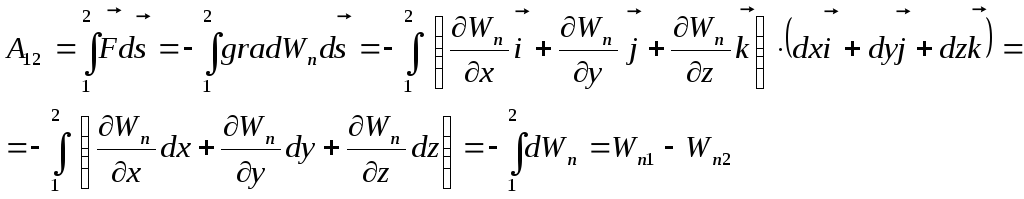
Следовательно, работа консервативных сил равна разности значений функции W_n в начальной и конечной точках пути, т.е. убыли потенциальной энергии.

Потенциальная энергия определяется с точностью до постоянной. Однако, это не имеет существенного значения, поскольку во все физические соотношения входит либо разность значений потенциальной энергии, либо ее производная по координатам.

Кинетическая энергия

Согласно формуле (3) для работы силы, получим также соотношение: .

Величина (5) называется кинетической энергией материальной точки.

Таким образом, мы приходим к формуле , (6)

из которой следует, что работа результирующей всех сил, действующих на материальную точку, расходуется на приращение кинетической энергии этой частицы.

Закон сохранения энергии

Полученный результат без труда обобщается на случай произвольной системы материальных точек.

Кинетической энергией системы называется сумма кинетических энергий материальных точек, из которых эта система состоит или на которые ее можно мысленно разделить: .

Напишем соотношение (3) для каждой материальной точки системы, а затем все такие соотношения сложим. В результате снова получим формулу, аналогичную (3), но для системы материальных точек.

, (7) где и - кинетические энергии системы, а под необходимо понимать сумму работ всех сил, действующих на материальные точки системы.

Таким образом мы доказали теорему (7): работа всех сил, действующих на систему материальных точек, равна приращению кинетической энергии этой системы.

Рассмотрим систему из n материальных точек, на которые действуют как консервативные так и неконсервативные силы. Найдем работу, которую совершают эти силы при перемещении системы из одной конфигурации в другую. Работа консервативных сил может быть представлена как убыль потенциальной энергии системы [(см. 4.8)]: .

Работу неконсервативных сил обозначим посредством А*. Согласно (7) суммарная работа всех сил затрачивается на приращение кинетической энергии системы , следовательно, или

.

Сумма кинетической и потенциальной энергии представляет собой полную механическую энергию Е системы: (8) Таким образом (9)

Очевидно, что если неконсервативные силы в системе отсутствуют, т.е. , то ее полная механическая энергия остается постоянной (сохраняется) т.е. Е = const. Эту теорему называют законом сохранения механической энергии, он утверждает: полная механическая энергия системы материальных точек в замкнутой системе, а также в не замкнутой системе, но находящихся под действием консервативных сил остается постоянной.

В такой системе могут происходить лишь превращения потенциальной энергии в кинетическую и обратно, но полный запас энергии системы измениться не может. При наличии неконсервативных сил (например, сил трения, сил сопротивления...) механическая энергия системы не сохраняется, она уменьшается, что приводит к ее нагреванию. Такой процесс называется диссипацией (рассеянием) энергии. Силы, приводящие к диссипации энергии, называются диссипативными.

Вывод закона сохранения энергии.

В основе закона сохранения энергии лежит такое свойство времени как однородность, т.е. равнозначность всех моментов времени, заключающаяся в том, что замена момента времени t₁ моментом времени t₂, без изменения значений координат и скоростей тел не изменяет механических свойств системы. Поведение системы, начиная с момента времени t₂ будет таким же, каким оно было бы, начиная с момента t₁.

Рассмотрим замкнутую систему, время однородно значит, состояние системы не должно явно зависеть от времени. Состояние системы определяется функцией Лагранжа. Поэтому частная производная от функции Лагранжа по времени равна нулю

Вычислим полную производную по времени

Поэтому L зависит от обобщенных координат обобщенных скоростей

Из уравнения Лагранжа

Поэтому

Отсюда

Функция Гамильтона:

Физический смысл:

Вычислим функцию Гамильтона для материальной точки в декартовой системе координат (10)

(11)

В классической механике потенциальная энергия от скоростей не зависит

Подставив (11) в (10) получим

более строгое доказательство, этого выражения проведено Эйлером.

Функция Гамильтониана равна энергии. Полная энергия системы сохраняется, энергия величина постоянная. Закон сохранения энергии один из фундаментальных законом, так как является следствием однородности времени.

4