МОТС / Часть2 / 21. Симплекс метод

21. Симплексный метод.

Симплекс-метод — алгоритм решения оптимизационной задачи линейного программирования путём перебора вершин выпуклого многогранника в многомерном пространстве. Метод был разработан американским математиком Джорджем Данцигом в 1947 году.

Идея симплексного метода состоит в том, что поставленная описательная задача переводится в математическую форму. Математическая формулировка задачи содержит уравнение целевой функции с указанием желаемого результата — определение минимума или максимума целевой функции; системы линейных ограничений, заданных равенствами или неравенствами. Полученное математическое описание приводят к матричному виду. Затем матричное описание задачи приводят к канонической форме. После того как система линейных уравнений приведена к канонической форме, приступают к решению задачи линейного программирования. Алгоритм решения этой задачи состоит из последовательности построения матриц. Каждый шаг решения приближает к получению желаемого результата.

В вычислительной схеме симплекс-метода реализуется упорядоченный процесс, при котором, начиная с некоторой исходной допустимой угловой точки (обычно начало координат), осуществляются последовательные переходы от одной допустимой экстремальной точки к другой до тех пор, пока не будет найдена точка, соответствующая оптимальному решению.

Алгоритм симплекс-метода

1. Приводим систему ограничений к каноническому виду (когда система ограничена). Причём в системе можно выделить единичный базис.

2. Находим первоначальный опорный план.

3. Строим симплексную таблицу.

4. В симплексной таблице проверяем вектора на отрицательность, т.е. оценки Zj – Сj записанные в 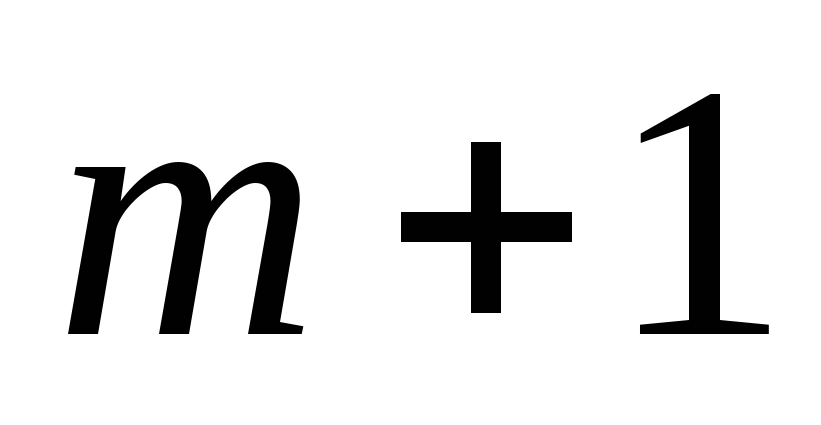строке должны быть ≤ 0 (на минимум), Zj – Сj ≥ 0 (на максимум). Если оценки удовлетворяют условиям оптимальности то задача решена.

5. Если для некоторых векторов нарушаются условия оптимальности, то необходимо ввести в базис вектор, которому соответствует:

max[θ_0j ( Zj – Сj )] ; min[θ_0j ( Zj – Сj )] ; θ_0j = min , где х_i > 0

Элемент вектора θ_j который соответствует θ_0j называется разрешающим; строка и столбец в которых он находится, называется направляющим, из базиса уходит вектор, стоящий в направляющей строке.

6. Найдём коэффициент разложения для всех векторов в новом базисе. Применим метод Джордано Гаусса

7. Проверим на оптимальный опорный план. Если оценка удовлетворяет условиям оптимальности, то задача решена, если нет, то выполняются пункты 5-7.