
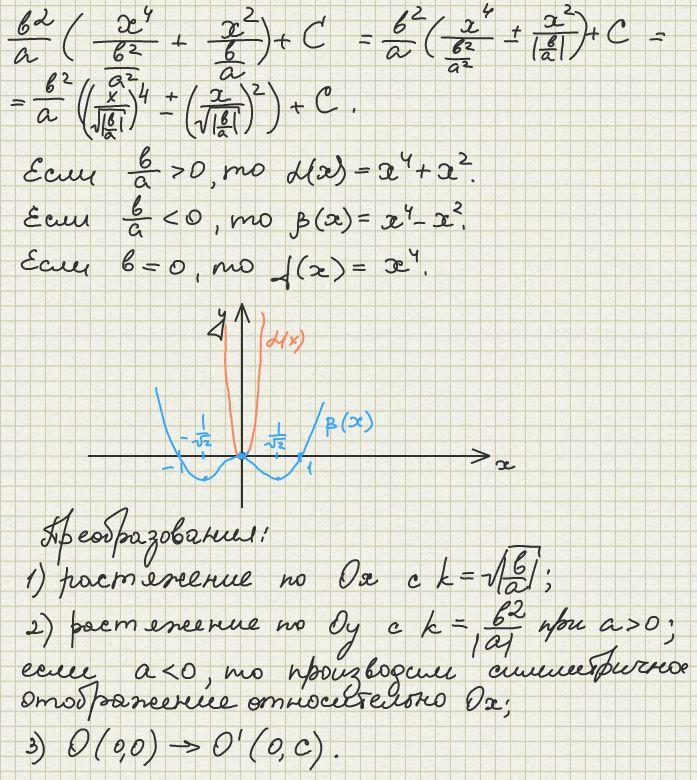
- •3. Если
- •4. Если
- •Класс целых рациональных функций.
- •4) Выводы:
- •Класс дробно-рациональных функций.
- •1) Дробно-рациональные функции, числитель которой представлен в виде многочлена второй степени.
- •2) Дробно-рациональные функции, знаменатель которой представлен в виде мрогочлена второй степени.
- •3) Дробно-рациональные функции, числитель и знаменатель которой представлен в виде многочлена второй степени.
Параграф 3. Элементарные геометрические преоьразования графиков функции.
Теорема 1. Пусть функция F(x)=f(x-a)+b, где a, b - положительные числа, и график функции f (x) известен. Тогда график функции F (x) можно построить с помощью параллельноо переноса графика функции f (x),птри котором точка начала координат имеет своим образом точку с координатами (a,b).
Доказательство.
1. Пусть точка М (х0,у0) лежит на графике функции f (x), тогда f (x0)=y0.
Закон параллельного переноса:
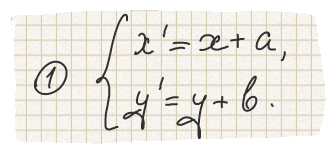
М' - образ точки М.
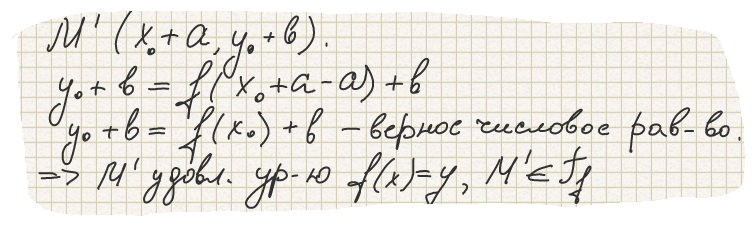
2.
Пусть точка
![]()
Тогда
координаты этой точки удовлетворяют
равенству: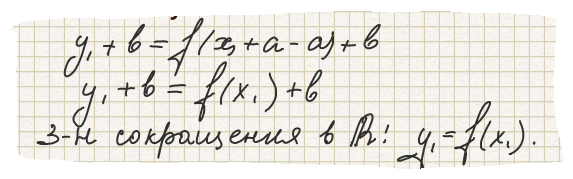
При параллельном переносе (1) точка М' имеет образ точку М, следовательно точка М (х1, у1) лежит на графике функции y=f (x).
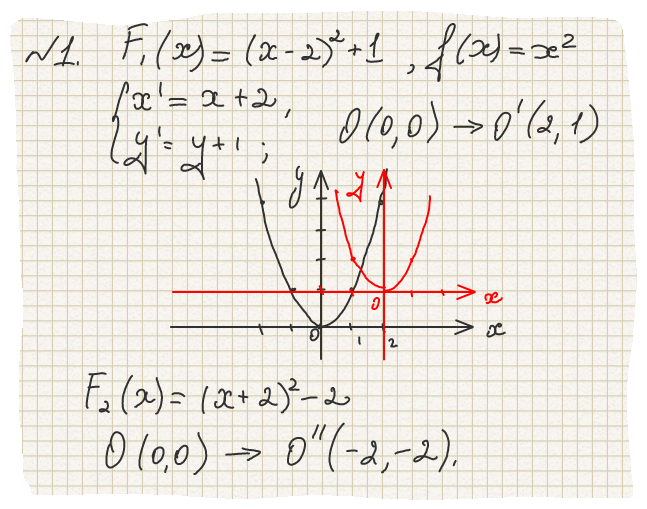








П













 равила
построения графика функции ,
зная график функции :
равила
построения графика функции ,
зная график функции :
1. Если число а> 0, то график функции смещается вправо на а единиц.
2. Если а <0, то график функции смещается влево на модуль а единиц.
3. Если b> 0, то график смезается вверх на b единиц. Если b <0, то график функции смещается вниз на модуль b единиц.











Т







 еорема
2. Пусть
функция задана
, где l, k отличны от нуля. Тогба график
функции F можно получить растяжением
графика f вдоль оси ординат с коэффициентом
l, а затем вдоль оси абсцисс с коэффициентом
k.
еорема
2. Пусть
функция задана
, где l, k отличны от нуля. Тогба график
функции F можно получить растяжением
графика f вдоль оси ординат с коэффициентом
l, а затем вдоль оси абсцисс с коэффициентом
k.
Правило трансформации функции .
1. Если l> 1, то осуществляется растяжение с коэффициентом l вдоль оси Оу.
2. Если 0 <l <1, то осуществляется сжатие графика с коэффициентом 1/l вдоль Оу.
3. Если k> 1, то осуществляется растяжение с коэффициентом k вдоль Ох.
4. Если 0 <k<1, то осуществляется сжатие с коэффициентом 1/k вдоль Ох
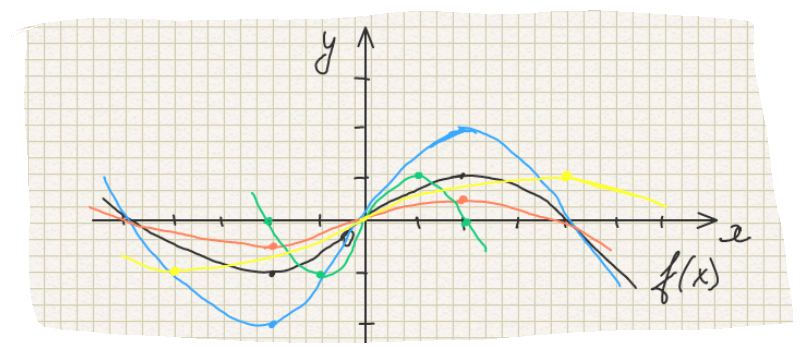
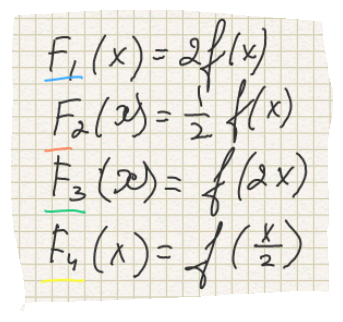
Следствия из теорем:
1. Если F задано формулой
![]() ,
,
то график F получается из графика f с помощью симметрии относительно оси Ох.
2. Если
![]() ,
,
то график F получается при помощи графика f с помощью симметрии относительно Оу.
3. Если
![]() ,
,
то график F получается при помощи графика f с помощью симметрии относительно начала координат.
4. Если
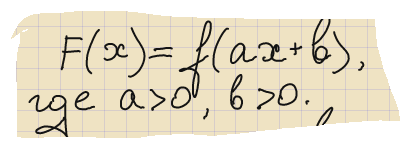 ,
,
то следует преобразовать формулу функции к виду
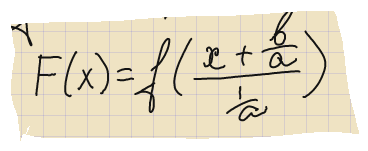 .
.
Следует сначала выполнить сжатие, а затем параллельный перенос графика влево.
Параграф 4. Геометрические преобразования как метод исследования рациональных функций.
Рациональные функции:
1. Целые - это функции, значения которых находятся посредством только трёх операций: сложения, вычитания, умножения, которые выполняются над переменной х и действительными числами. Представляют целые рациональные функции в виде многочлена от одной переменной х, записанного по убыванию степеней:

2. Дробно-рациональные - функции, которые можно представить в виде отношения двух многочленов, записанных по убыванию степеней:
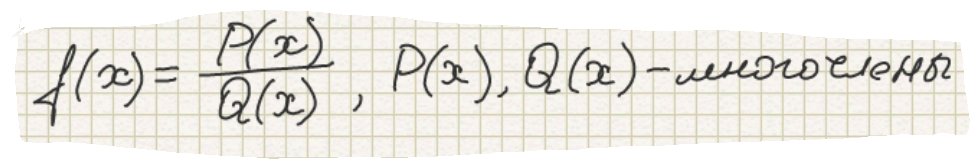
Класс целых рациональных функций.
1. Функции целых положительных значений.
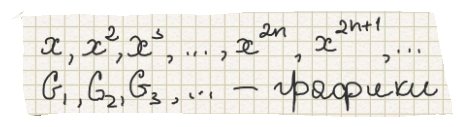
1) у=х.

G1 - прямая.
2) у=х^2.

Исследуем функцию на выпуклость.

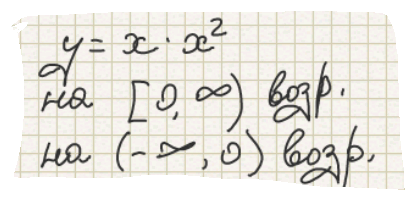
G2 - парабола.
3) у=х^3.
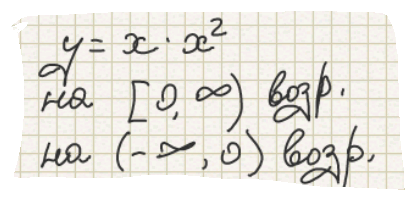
Исследуем на выпуклость.
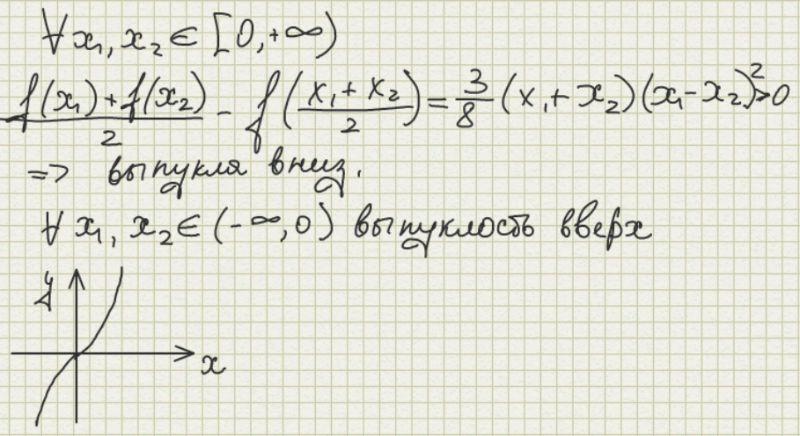
G3 - кубическая парабола.
4) Выводы:
Функции вида х^2n имеют схожие свойства с функцией у=х^2, график функции напоминает параболу, ветви тем ближе к осям, чем больше показатель степени.
Функции вида х^2n+1 имеют схожие свойства с функцией х^3, график напоминает кубическую параболу, лишь ветви ближе распологаются к осям, чем выше показатель степени.
2. Линейная функция.
Линейной называют функцию, заданную формулой y=kx+b.
График линейной функции можно получить при помощи растяжения вдоль Оу с коэффициентом k и параллельного переноса на b единиц вверх графика функции y=x.
Графиком линейной функции является прямая.
Если k> 0, то функция возрастает; если же k <0, то функция будет убывать.
3. Квадратичная функция.
Квадратичной функцией называют функцию, заданную формулой y=ax^2+bx+c, где a, b, c отличны от нуля.
Выполним необходимые преобразования:

4. Функция-многочлен третьей степени.
Функцией-многочленом третьей степени называют функцию вида:
![]()
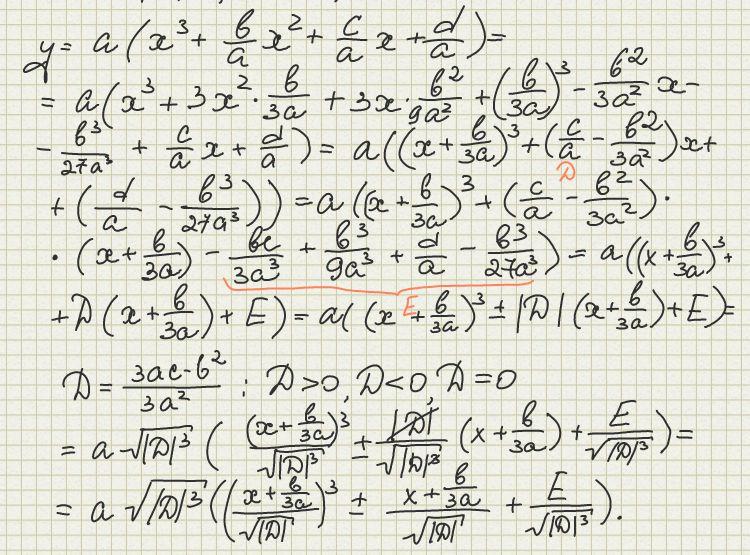
Выделяем три базовые функции:
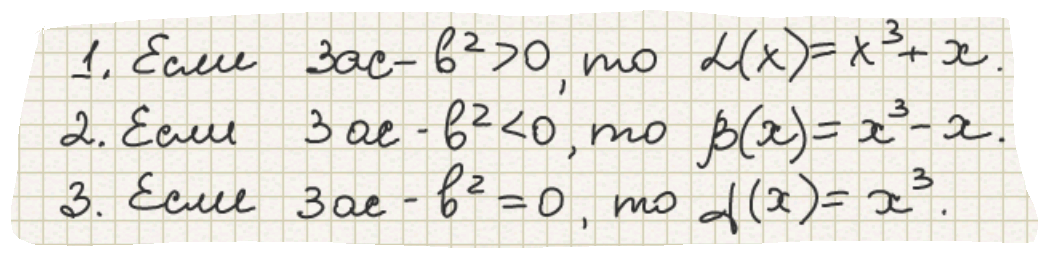
Геометрические преобразования следует выполниьь в следующей последовательности:
1. На основании теоремы 2 выполняем иастяжерие базовых функций вдоль Ох с коэффициентом корень квадратный из модуля D.
2. По теореме 1 выполняем параллельный перенос, при котором точка начала координат перейдёт в точку:
![]() .
.
3. Выполняем растжение вдоль Оу, если а> 0:
![]() .
.
4. Если а <0, то мы осуществляем симметрию относительно Ох.
Исследуем аналитически свойства базовых функций.
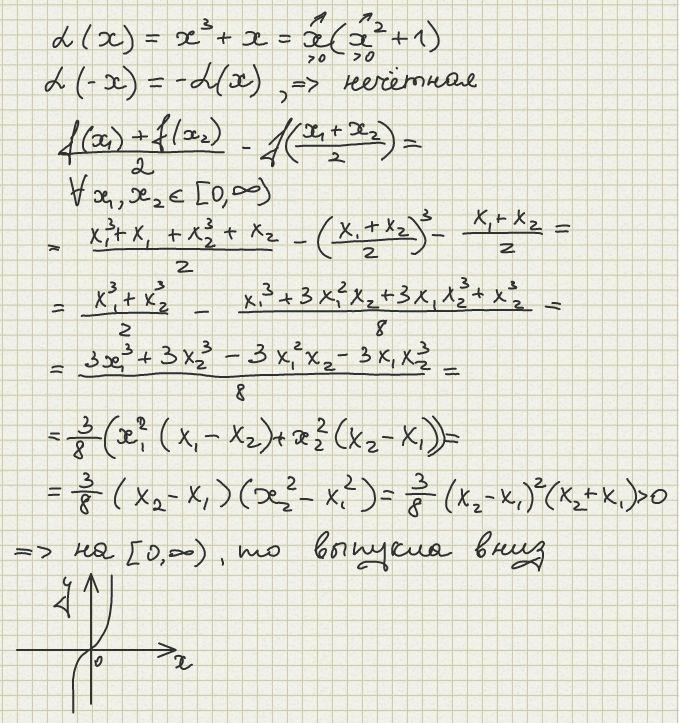


5. Функция-многочлен четвёртой степени (биквадратный многочлен).
Функция от биквадратного многочлена называется функция вида
![]()
Класс дробно-рациональных функций.
1. Функции целых отрицательных степеней.
Функцию целых отрицательных степеней называют функцию вида:
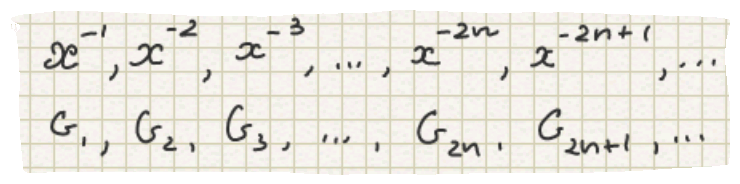
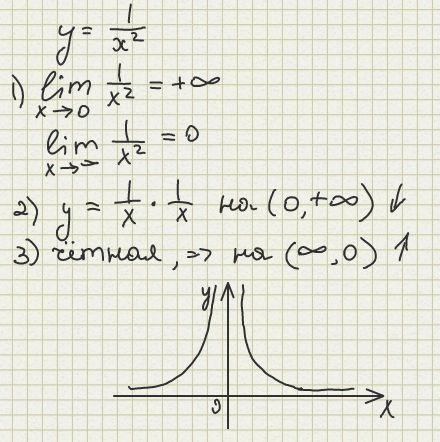
1) y=1/x.

G1 - гипербола.
2) y=1/x^2.
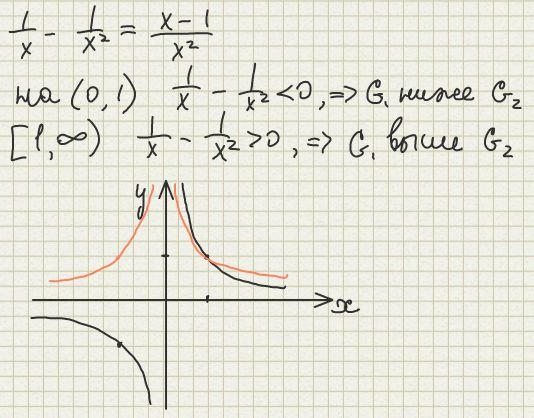
Выясним взаимное расположение графиков G1, G2.
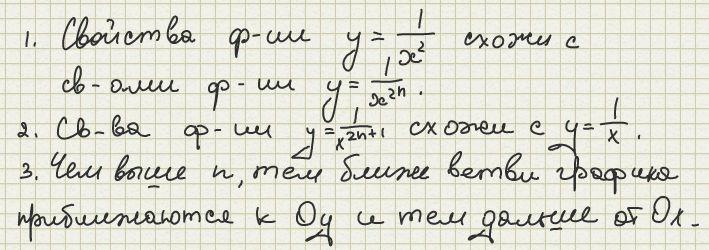
2. Дробно-линейные функции.
Дробно-линейными функциями называются функции вида
![]()
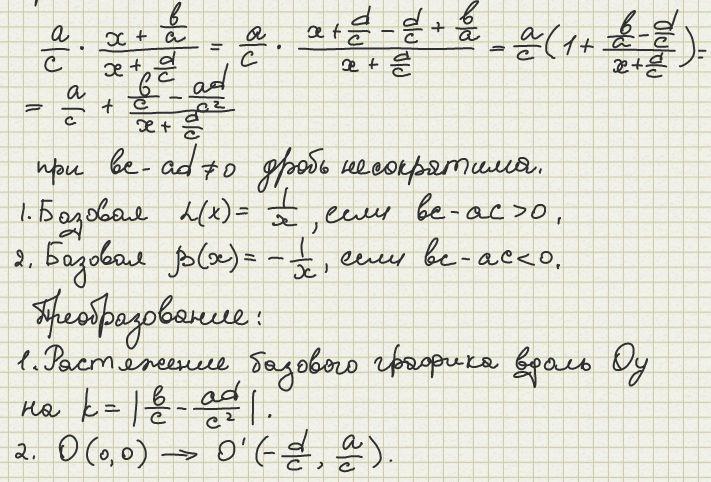
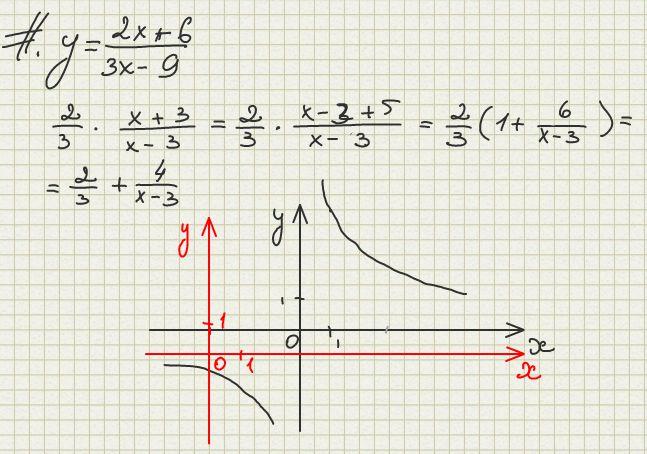
3. Дробно-рациональные функции, числитель и/или знаменатель которых представлен (ы) в виде многочлена второй степени.
