praktikum_po_lineinoi_algebre

41

x(i),(i =1,...,r) i-е свободное неизвестное равно 1, а остальные

свободные неизвестные равны 0, а xr(i+)1,...,xn(i) (главные

неизвестные) через них однозначно выражаются. Система решений

м		(i)ь		(i =1,...,r)	называется фундаментальной (или базисной)
нx			э
о			ю

системой решений (ФСР) вышеуказанной однородной системы уравнений.

Теорема. Любое решение x однородной системы уравнений однозначно представляется в виде некоторой линейной комбинации решений ФСР: x =a1x(1) +...+ar x(r) при некоторых

числах a1,...,ar .

Следствие. ФСР полностью определяет множество решений однородной системы уравнений. Для решения такой системы достаточно найти её ФСР.

Замечание. Если свободные неизвестные имеют другие индексы, то ФСР строится аналогично.

жз x1 цч

Легко видеть, что задача поиска всех решений x =з...ч

зиxn чш

векторного уравнения (*) сводится к задаче поиска всех решений

жз x1 цч

x =з...ч однородной системы уравнений, матрица которой

зиxn чш

составлена (по столбцам) из координат заданных векторов

42

а1,...,аn . Как отмечалось выше, множество решений однородной системы уравнений полностью определяется её ФСР. Таким образом, задача нахождения всех линейных соотношений между векторами а1,...,аn сводится, по сути, к нахождению r базисных соотношений между ними, задаваемых при помощи ФСР соответствующей однородной системы.

Во всех приведённых ниже примерах требуется выяснить,

является ли заданная система векторов линейно зависимой, и в случае линейной зависимости найти базисные соотношения между векторами.

Пример 1. Даны вектора a,b,c,d,e (их координаты — столбцы

ж

a

b

c

d

e

ц

- 2

-3

1

1

1

матрицы А):

з

ч

з 4

0 - 2 1 - 2ч= A.

з

6

3

-3

0

ч

з

-3ч

и

ш

Запишем:

x1

+ x2

+ x3

+ x4

+ x5

=

(**).

a

b

c

d

e

0

Перепишем векторное равенство (**) в виде

ж- 2

ц

ж-3 ц

ж

1 ц

ж1 ц

ж 1

ц ж0 ц

з

ч

з

ч

з

ч

з ч

з

ч з ч

x1з 4 ч + x2з 0 ч + x3з- 2 ч + x4з1 ч + x5з- 2 ч = з0 ч

з

6

ч

з

3

ч

з

ч

з ч

з

ч з ч

и

ш

и

ш

и

-3 ш

и0 ш

и-3

ш и0 ш

м- 2x1 - 3x2 + x3 + x4 + x5 = 0

п

- 2x3 + x4 - 2x5 = 0 .

или н4x1

п

-3x3 -

3x5 = 0

о6x1 +3x2

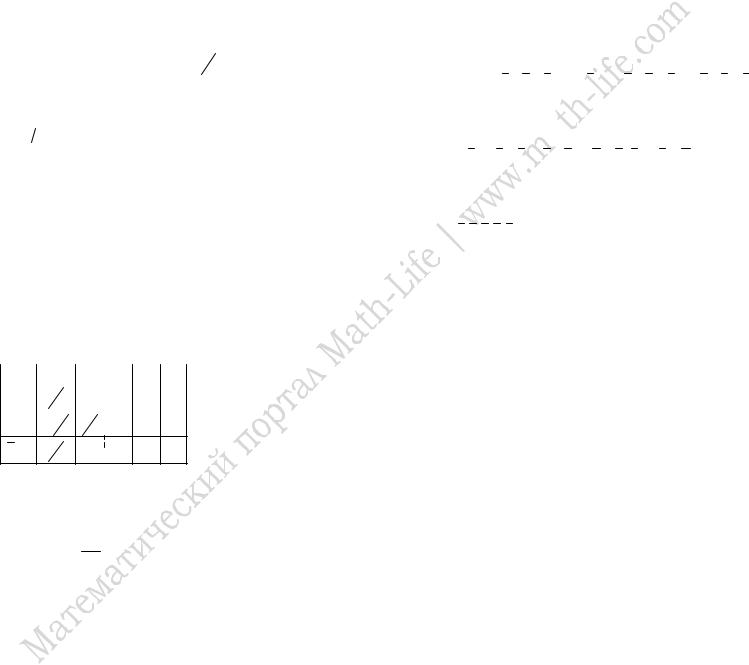
Решим эту однородную систему уравнений, т.е. найдём её ФСР.

Сначала по методу Гаусса найдём общее решение системы:

43

ж- 2

-3

1

1

1 ц

ж - 2 -3

1

1

1 ц

з

ч

Ю

A ® з 0 - 6 0 3 0 ч ®

з

0

1

0

-

1

0

ч

з

ч

з

ч

0

- 6

0

3

и

2

ш

и

0 ш

мx = -

3x2

+

x3

+

x4

+

x5

м- 2x -3x

+ x

+ x

+ x

= 0

п

1

2

3

4

5

п

2

2

2

2 Ю

Ю н

1

Ю н

о

x2 - x4 2 = 0

п

x2

=

x4

п

о

2

мx =

1

(x

3

- x

4

+ x

5

)

п

1

2

п

x

п

4

(***)

Ю н

x2 =

.

2

п

пх3,х4,х5 - любыечисла

п

о

Здесь главные неизвестные — x1, x2, свободные — x3, x4, x5.

Для построения						ФСР	х(1)	,	х(2)			,	х(3)		составим следующую
таблицу.
						x1	x2				x3		x4		x5
					(1)	1	0				1		0		0
			x			2
				(2)		- 1	1						1		0
		x									0
						2	2

(3)1

x2 0 0 0 1

Столбцы таблицы соответствуют неизвестным х1,...,х5 (пунктирная линия разделяет главные и свободные неизвестные — для наглядности), а строки — искомым решениям. Поясним, как

получено, например, решение х(1) : выбираем х3 =1,х4 = 0,х5 = 0,

а х1 и х2 определяем однозначно по формулам (***).

44

Подставим теперь в (**) три найденных набора x1,…,x5,

получив три базисных соотношения между векторами:

0,5a + c = 0, -0,5a + 0,5b + d = 0, 0,5a + e = 0 .

Умножая левые и правые части этих равенств на "2", получим окончательный ответ.

Ответ: a + 2c = 0, -a + b + 2d = 0, a + 2e = 0.

Рекомендуется проверить полученные соотношения.

Отметим также, что любое линейное соотношение вида (**)

между а,b,c,d,е однозначно представляется в виде некоторой линейной комбинации полученных соотношений в том смысле, что

=a

Ч

х(1)

+a

Ч

х(2)

+a

Ч

х(3)

при некоторых числах a ,a

,a

.

х

1

2

3

2

3

1

Пример 2. Даны

,

,

(их координаты — столбцы матрицы А):

а

b

c

ж

a

b

c

ц

1

1

1

A =

з

ч

. Запишем:

з2

2

2 ч

з

3

-2

ч

з2

ч

и

ш

x1

+ x2

+ x3

=

.

(****)

a

b

c

0

А ®

ж1 1 1

ц

®

ж1 1 1

ц

мx + x

+ x

= 0

з

ч

з

ч Ю н 1

2

3

Ю

з

ч

з

0 1 - 4

ч

о

x2 -

4x3

= 0

и2 3 -2

ш

и

ш

мx

1

= -5x

3;x ,x

-главные, x

-свободное неизвестное.

Ю н

оx2 = 4x3

1

2

3

Для нахождения ФСР, положим х3 =1 и найдём х1 = -5 и

х2 = 4. Подставив в равенство (****) эти значения х1, х2 и х3 ,

получим окончательный ответ.

45

Ответ: -5a + 4b + c = 0 .

Пример. Даны вектора a,b,c (их координаты — столбцы

нижеприведённой матрицы).

Повторяя рассуждения примера 1, придём к задаче решения

однородной системы уравнений с заданной матрицей.

	a	b	c		ж1 2		-1ц	мx1 + 2x2 - x3 = 0
ж				ц
	1	2
з			-1ч		з		ч	п	- x2 +3x3 = 0 Ю x1 = x2 = x3 = 0.
з 1		3	2 ч		® з0	-1 3 ч Ю н
з				ч	з0	0	-3ч	п	-3x	3	= 0
з	- 2	- 4		ч	и		ш	о
и			-1
				ш

Следовательно, все неизвестные — главные, нет свободных; у

системы уравнений есть только нулевое решение x = (0,0,0).

Поэтому исходная система векторов линейно независима.

Ответ: система векторов линейно независима.

Выводы. Чтобы найти связь между векторами необходимо:

1)

Записать матрицу А, столбцы которой — координаты

векторов;

2)

Решить однородную систему уравнений с матрицей А

методом Гаусса и затем найти ФСР.

3)

Подставить найденные

решения

из ФСР

в уравнение

x1

+ x2

+...+ xn

=

,

получив r

базисных

соотношений

a1

a2

an

0

между векторами (r равно числу свободных неизвестных); если r=0, то вектора — линейно независимы.

46

Задачи для самостоятельного решения

Найти зависимость между векторами (если вектора линейно

зависимы):

мж1ц

з чп

п

=

з2ч

м

ж

1 ц

а

з

3ч

п 1

м

ж

1 ц

п

з

-2

ч

п

з ч

п

а = з

ч

а =

з

ч

п

з

ч

1

з

ч

п

1

и

4ш

п

и

-1ш

п

з

3

ч

п

п

и

ш

п

ж

4ц

п

ж

-2ц

п

з

ч

а

2

= з

ч

п

ж

2 ц

з

ч

п

з3ч

п

и

-2ш

п

з

ч

1) на2 =

з

2

ч; 2)

н

; 3)

на2

= з-3ч; 4)

п

з

ч

п

ж

-1ц

п

з

1

ч

а

3

=з

ч

п

з

1

ч

п

з

ч

п

и

ш

и

ш

и

-3ш

ж

-1ц

п

п

п

п

ж

5ц

п

=

ж1ц

п

=

з

-3

ч

п

з

ч

п

а4

з

ч

а

з

ч

5ч

з

ч

п

3

п

=

з

о

и1ш

п

з

2

ч

а3

з

ч

о

и

ш

п

з

5ч

п

з

5

ч

о

и

ш

м

ж1ц

м

ж

2ц

п

з

ч

п

з

ч

па1

=з2ч

па1

=з3ч

м

ж

1ц

п

з

ч

п

з

ч

и

2ш

и

0ш

п

з ч

п

ж

1ц

п

ж

1ц

па1

=з2ч

п

п

п

з ч

5)

п

з

ч

п

з

ч

п

и

1ш

.

на2

= з2ч ; 6)

на2

=з0ч; 7)

н

ж

0ц

п

з

ч

п

з

ч

п

и

3ш

и

4ш

з

ч

п

п

па2

ж

-1ц

ж

0ц

=з3ч

п

п

п

з

4ч

з

ч

з

ч

п

п

п

и

=з

-2ч

= з1ч

о

ш

па3

па3

п

з

ч

п

з

ч

о

и

-6ш

о

и

2ш

мж1ц

з чп

па1 =з2			ч
п	з	3	ч
	и		ш
п

пж0ц

пз ч на2 =з1ч;

пзи2чш

пж1ц

пз ч па3 = з1ч

пзи1чш

о

47

ма

= а + а

п

3

1

2

Ответы: 1)

а3 = а1 +а2 ; 2)

; 3),6),7) — вектора

н

= -

а2

п

а4

о

2

линейно независимы; 4) а1 = а2 +а3 ; 5) а3 = 3а1 - 4а2 .

Занятие 8.

Скалярное произведение векторов.

Определение. Скалярным произведением векторов a и b

ж Щ ц

называется число a Чb = a Ч b Чcosззa,bчч .

иш

Свойства скалярного произведения векторов.

1)aЧb = bЧа;

2)laЧb = aЧlb = l(aЧb);

3) (a + b)Чc = aЧc + bЧc ;

4) aЧa і 0;aЧa = 0 Ы a = 0.

Некоторые формулы.

2

1)

a Чa =

a

Ю

a

= aЧa ;

ж

Щ

ц

aЧb

2)

з

ч

=

;

cos

a,b

з

ч

a

Ч

b

и

ш

3)

^

Ы

Ч

= 0;

a

b

a

b

48

ж

Щ

ц

Ч

a

b

4)

Пр

b

=

b

Чcosз

a

,

b

ч

=

(Пр

b

— проекция вектора

b

на

a

з

ч

a

a

и

ш

вектор

);

a

жx

ц

жx

ц

з

1

ч

з

2

ч

5)

если

a =з y1 ч,b = зy2 чЮ aЧb = x1 Чx2 + y1 Ч y2 + z1 Чz2 .

з z

ч

зz

2

ч

и

1

ш

и

ш

Последняя формула справедлива для ортонормированного

базиса.

Задачи.

I.

Даны два вектора

и

такие, что

m

n

ж

Щ

ц

m

=

n

=1,j = з

m

,

n

ч =120o

;

a

= 2

m

+ 4

n

,

b

=

m

-

n

з

ч

иш

ж

Щ

ц

Найти: 1)

a

; 2)

b

; 3)

a

Ч

b

; 4)

з

a

,

b

ч

; 5)

S—площадь

з

ч

и

ш

параллелограмма, построенного на векторах

и

; 6)

Пр

.

a

b

a

b

Имеем:

a2 = aЧa = (2m + 4n)Ч(2m + 4n)= 4mЧm +16mЧn +16n Чn =

1)

2

2

= 4

m

+16Ч

m

Ч

n

Чcosj +16

n

= 4 -8 +16 =12 Ю

a

= 12.

2
b = bЧb = (m - n)Ч(m - n)= mЧm - 2mЧn + n Чn =
2)	2
2
= m	- 2Ч m Ч n Чcosj + n =1+1+1= 3 Ю b = 3.

49

Ч

= (2

+ 4

)Ч(

-

)= 2

Ч

+ 2

Ч

- 2

Ч

=

3)

a

b

m

n

m

n

m

m

m

n

n

n

= 2

2

Ч

Чcosj - 4Ч

2

= 2-1-4 = -3.

m

+2Ч

m

n

n

ж

Щ

ц

ж

Щ

ц

a Чb

-3

1

4)

з

ч

з

ч

o

a = cosзa,b

ч

=

=

= -

2

Юa =

зa,b

ч

=120 .

a

Ч

b

12 Ч 3

и

ш

и

ш

5)S = a Ч b Чsina = 12 Ч 3 Ч 1- 14 = 33. (sina = 1- cos2 a ;

не путать α с φ!)

6) Пр

a

Ч

b

-

3

a

=

=

= -

3.

b

b

3

Пример 2. Даны координаты вершин треугольника ABC:

A(-1,-2,4), B(-4,-2,0), C(3,-2,1). Найти: 1) BA , BC ; 2) РB; 3) SDABC ;

4) ПрBC BA; 5) hBC — высоту, опущенную на BC.

Имеем:

ж

3

ц

ж7

ц

з

ч

з

ч

1) BA=з

0

чЮ

BA

=5;BC =з0

чЮ

BC

= 50;

з

4

ч

з

1

ч

и

ш

и

ш

2)

Ч

= 25 Ю cosРB =

BA

Ч

BC

=

25

=

1

Ю РB =

p

;

BA

BC

BA

Ч

BC

5Ч 50

2

4

1

p

1

Ч

5

=12,5;

3)

SD

=

Ч

Чsin

=

50

BA

BC

2

4

2

2

Ч

=

25

5

;

4)

Пр

BA

BC

=

=

BA

BC

BC

50

2

50

5) S

1

=

1

Ч

Ч

Чsin

p

Ю h

=

Ч

2

=

5

2

.

=

h

Ч

D

BC

AB

BC

AB

2 BC

2

4

BC

2

2

Пример 3.

Упростить выражение:

ж

2

2

ц

(3a + b)Ч(a - 2b)+ (5b -a)Чb

-3з

a

+

b

ч.

Имеем:

и

ш

ж

2

2

ц

= 3aЧa + aЧb - 6aЧb -2bЧb +

(3a + b)Ч(a - 2b)+ (5b -a)Чb -3з

a + b

ч

иш

																2						2						2										2						2						2
+5bЧb -aЧb -3												a				-3		b				= 3		a				- 6aЧb + 3						b				-3		a				-3		b				=

= -6aЧb.

Задачи для самостоятельного решения

ж

Щ

ц

p

з

ч

1)

Даны вектора m и

n такие, что

m

= 2,

n

=1,j =

m,n

=

з

ч

3

и

ш

и

по

ним

построены

вектора

= 2

+

,

=

- 2

.

Найти

a

m

n

b

m

n

ж

Щ

ц

a =

з

a

,

b

ч,

a

,

b

,

a

Ч

b

, S — площадь параллелограмма, построенного

з

ч

и

ш

на a,b.

2) Даны точки A(4,1,2),B(2,3,0),C(1,3,-1). Найти SDABC

(площадь треугольника АВС), hBA (высоту, опущенную на сторону

ВА), cosРB.

3) Даны вектора a = i + j + 2k,b = i - j + 4k . Найти Прba,Прab .

4) Упростить выражение (2i - j)Ч j + (j -2k)Чk + (j - 2k)Ч(i -2k).

51

5) Даны три вершины параллелограмма ABCD:

A(-3,-2,0),

В(3,-3,1),С(5,0,2). Найти четвёртую вершину D(x,y,z).

Ответы:

1)

=

= 2,

Ч

= 3,a = arccos

3

,S = 6

;

a

21,

b

a

b

2

2

21

2) S

=

2

,cosРB = -

2

; 3) Пр

8

,Пр

=

8

;

DABC

=

2,h

a

=

b

b

BA

6

6

8

a

6

4) 2; 5) D(-1,1,1).

Занятие 9.

Векторное и смешанное произведение

векторов.

Определение. Векторным произведением векторов a и b

ж

Щ

ц

называется вектор

c

=

a

ґ

b

такой, что: 1)

с

=

a

Ч

b

Чsinз

a

,

b

ч

; 2)

c

з

ч

и

ш

перпендикулярен плоскости векторов a и b; 3) a,b и c — правая тройка векторов (см. рисунок).

Геометрический смысл модуля векторного произведения: с

равен площади параллелограмма, построенного на векторах a и

b.

52

Свойства векторного произведения.

1)

aґb = -bґa;

с

2)

(l

)ґ

= l(

ґ

)=

ґ(l

);

a

b

a

b

a

b

3)

(

+

)ґ

=

ґ

+

ґ

;

a

b

c

a

c

b

c

b

4)

||

Ы

ґ

=

;

Рис. 7

a

b

a

b

0

a

жa

x

ц

жb

ц

з

ч

з x

ч

{i, j,k}Ю c = aґb =

5)

пусть

a = зay ч, b =зby ч в

базисе

з

ч

з

ч

иaz

ш

иbz

ш

i

j

k

=

ax

ay

az

. Последнее

выражение

является символической

bx by bz

записью

=

ґ

в

виде

определителя,

который

позволяет

с

a

b

получить

координаты

вектора

в базисе {i,

,

}.

Для этого

c

j

k

необходимо разложить этот определитель по 1-ой строке.

Определение.

Смешанным

произведением 3-х векторов

,

,

называется

число (

ґ

)Ч

.

В базисе {i,

,

} смешанное

a

b

c

a

b

c

j

k

произведение векторов

,

,

находится по формуле

a

b

c

(

ґ

)Ч

=

ax

ay

az

.

a

b

с

bx by bz

cx

cy

cz

53

Геометрический

смысл

модуля

смешанного

произведения:

(

ґ

)Ч

равен

объёму

параллелепипеда, построенного

на

a

b

c

векторах

,

,

(здесь берётся модуль числа!).

a

b

c

Утверждение. 1) Векторы

,

,

компланарны Ы (

ґ

)Ч

= 0 ;

a

b

c

a

b

c

2)

векторы

,

коллинеарны Ы

ґ

=

.

a

b

a

b

0

Пример 1. Даны четыре точки A(5,1,-4), B(1,2,-1), C(3,3,-4),

D(2,2,2).

Найти

1)

SDBCD;

2)

Vпирамиды ABCD ;

3)

Vпараллелепипеда на

,

,

; 4) hBCD

— высоту в пирамиде ABCD,

AB

AC

AD

опущенную на грань BCD.

Найдём

(

)Ч

-4

1

3

= -24ЮVпарал.

(

)Ч

ґ

=

-2

2

0

=

ґ

= 24,

AB

AC

AD

AB

AC

AD

-3

1

6

V

=

1

V

=

24

= 4;

пирамиды

6

парал.

6

ж

2 ц

ж1ц

S

=

1

ґ

,

=

з

1 ч,

=

з

0

чЮ

BC

BD

BC

BD

DBCD

з

з

2

ч

ч

з

ч

з

3

ч

и-3ш

и

ш

i

j

k

1

-3

2

-3

2

1

BCґBD =

2 1 -3

= i

- j

+ k

=3i-9j -k Ю

0

3

1

3

1

0

1

0

3

1

=

.

Ю S

=

91

DBCD

9+81+1

2

2

54

С другой стороны,

V

= 1 h

ЧS

DBCD

Ю h

=

3Vпирамиды

= 24 .

пирамиды

3

BCD

BCD

SDBCD

91

Выводы.

1) SD,Sпараллелограмма = 2SD

ищем

через векторное

произведение соответствующих векторов; высоту в треугольнике

ищем, используя формулу геометрии: SD = 1 hЧа , где а —длина

2

стороны, на которую опущена высота.

2) Vпараллелепипеда ищем через смешанное произведение

1

соответствующих векторов; Vпирамиды = 6 ЧVпараллелепипеда ; высоту

в пирамиде ищем, используя формулу:

V	=	1	ЧhЧS , где S — площадь грани (т.е.
пирамиды	3

треугольника), на которую опущена высота);

Vпараллелепипеда = h ЧS , где S — площадь основания, (т.е.

параллелограмма), на которое опущена высота.

Задачи для самостоятельного решения

1) Даны точки А(1,-2,8),В(0,0,4),С(6,2,0). Найти SDABC

(площадь треугольника АВС), используя векторное произведение, и

hAC (высоту треугольника АВС, опущенную на сторону АС).

53

ж

Щ

ц

p

з

ч

2)

Даны вектора m и n , такие что

m

=1,

n

= 2,j =

m,n

=

,

з

ч

4

и

ш

и по

ним

построены вектора

=

+

,

= 2

-

. Найти

S —

a

m

n

b

m

n

площадь параллелограмма, построенного на векторах

,

.

a

b

3)

Даны точки

A(2,0,0),B(0,3,0),C(0,0,6),D(2,3,8). Найти

V

—

объём

пирамиды

ABCD,

hABC —

высоту этой

пирамиды,

опущенную на грань АВС.

4)

Доказать, что точки А(1,2,-1),В(0,1,5),С(-1,2,1),D(2,1,3)

лежат в

одной плоскости.

ж 2

ц

ж

1 ц

ж

3

ц

з

ч

з

ч

з

ч

5)

Доказать, что вектора

a = з-1ч,b = з

2 ч,c =з-4ч

лежат

з

ч

з

ч

з

7

ч

и 2

ш

и

-3ш

и

ш

в одной плоскости.

2

Ответы:

1) S = 7

5,hAC

=

21

;

2) S = 3

2

;

3)

V =14,

3

hABC = 14 ; 4),5) показать, что смешанное произведение векторов

AB,AC,AD (или a,b,c ) равно нулю.

54

Занятие 10.

Плоскость в пространстве.

Пусть M0(x0,y0,z0) — фиксированная точка плоскости p , а

ж Aц з ч

M(x,y,z)—любая точка этой плоскости, N =зBч — вектор

зиCчш

нормали к плоскости p , т.е. N^p .
z
	N
M0		p
M0
M
		y

xРис. 8.

1)Уравнение плоскости, проходящей через точку M0 , с вектором нормали N :

A(x - x0)+ B(y - y0)+C(z - z0) = 0.

2)Если мы раскроем скобки в предыдущем уравнении и приведём подобные члены, то получим общее уравнение плоскости:

Ax + By +Cz + D = 0, где D = -Ax0 -By0 -Cz0 .

Если один из коэффициентов A,B или C равен нулю, то плоскость p параллельна соответствующей координатной оси.

Если равны нулю два коэффициента, то p параллельна

57

соответствующей координатной плоскости. Если D=0, то плоскость p проходит через начало координат О(0,0,0).

3) Уравнение плоскости p , проходящей через 3 точки

M1(x1,y1,z1),M2(x2,y2,z2),M3(x3,y3,z3) можно получить

следующим	образом:	N = M1M2 ґM1M3,M0 є M1	и
воспользоваться формулой из пункта 1).

4)Углом между плоскостями p1 и p2 называется наименьший из двугранных углов, образованных p1 и p2 . Как легко заметить, в

силу данного определения 0 Јj Ј p . Следовательно, cosj > 0

2

и cosj =

N1 ЧN2

.

Ч

N1

N2

5)

Плоскости p1

и p2

перпендикулярны

в том и только том

случае, когда

Ч

= 0 , т.е. A1 Ч A2 +B1 ЧB2 +C1 ЧC2 = 0 .

N1

N2

6)

Плоскости p1

и p2

параллельны в том и только том случае,

когда

= l

(λ — число), т.е.

A1

=

B1

=

C1

.

N

2

N

1

A2 B2

C2

7)

Плоскости p1

єp2 (т.е. совпадают)Ы

A1

=

B1

=

C1

=

D1

.

A2

B2

C2 D2

8)

Расстояние

d

от

точки M1(x1,y1,z1)

до

плоскости p

(p : Ax + By +Cz + D = 0 ):

d = Ax1 + By1 +Cz1 + D .

A2 + B2 +C2

58

Пример 1.

Написать уравнение

плоскости p ,

проходящей

через точку M0(1,-2,0) и ось Oz.

Уравнение искомой плоскости имеет вид

Ax +By = 0 (C=D=0,

так как p

проходит через OZ). Пусть

x0 =1,y0 = -2,z0 = 0. Тогда,

подставив

эти

координаты

в

уравнение,

получим:

A - 2B = 0 Ю A = 2B

(пустьB =1Ю A = 2) Юp :2x + y = 0 .

Пример 2.

Написать уравнение

плоскости p ,

проходящей

через точку M0(4,-7,6) и перпендикулярной оси ОХ.

ж

1ц

з

ч

Так как p^ОХ ,

то

можно взять

N =з0чЮp : Ax+ D = 0.

з

ч

и

0ш

Подставим координаты точки М0

в это уравнение. Получим, что

4A+D=0. Возьмём A =1Ю D = -4 Ю p : x - 4 = 0 .

Пример 3.

Написать уравнение

плоскости p ,

проходящей

через точку M0(0,1,-1) , причём p ^p1,p ^p2 , где

p1 : 2x - y + 3z -1= 0, p2 : x + 2y + z = 0.

Так как p ||

,p ||

, то в качестве вектора нормали к искомой

N1

N2

плоскости можно взять следующий вектор

i

j

k

=

ґ

=

2

-1

3

= -7i +

+ 5

Ю

= (-7,1,5) Ю

N

N1

N2

j

k

N

1

2

1

Ю p : -7(x -0)+1(y -1)+ 5(z +1).

59

Пример 4.

Написать уравнение плоскости p , проходящей

через точки M1(3,-1,2),M2(4,-1,-1),M3(2,0,2).

Пример 5.

Написать уравнение плоскости p , проходящей

через точки M1(2,2,0)иВ(4,0,0)

и параллельной оси OZ.

Уравнение

плоскости p

должно иметь следующий вид:

Ax + By + D = 0 (C = 0,так какp ||OZ).

Кроме

того,

2А + 2В +D = 0 (таккак M1 Оp)

и

4A + D = 0 (таккак M2 Оp).

Разделив каждое из получившихся двух уравнений на D, получаем

систему

м2A

2B

мA

1

п

+

+1

= 0

п

= -

x

y

п

п

4 Ю -

н D D

Ю нD

-

+1= 0 Ю p : x + y - 4 = 0 .

п

4A

пB

1

4

4

п

+1= 0

п

= -

D

4

о

оD

Задачи для самостоятельного решения.

1)

Написать уравнение плоскости p , проходящей через точку

М0(1,1,-2)

и:

ж

1ц

з

ч

а)

имеющей нормаль N =з2ч;

з

ч

и

3ш

б)

проходящей через ось OZ;

в)

параллельной плоскости p1 : x + y -2z +1= 0 ;

г)

перпендикулярной

плоскостям p1 : x + y - z +1= 0

и

p2 :3x - y + 4z -1= 0;

д)

параллельной оси OZ и проходящей через точку М1(2,3,0);

				60
е)	проходящей через точки М1(1,2,3)				и М2(1,3,7).
2)	Найти	угол j	между	плоскостями p1 :3y - z = 0 и
p2 : 2y + z = 0.
3)	Найти	расстояние	d от	точки	М0(5,1,-1) до плоскости
p : x -2y - 2z + 4 = 0 .

Ответы:

1)а) p : x + 2y +3z + 3 = 0 ; б) p : y - x = 0 ;

в) p : x + y -2z - 6 = 0; г) p :3x -7y - 4z - 4 = 0;

д) p : -2x + y +1= 0; е) p : x -1= 0 .

3) j = p ; 3) d=3.

4

Занятие 11.

Прямая в пространстве и на плоскости.

Совместные задачи на прямую и плоскость.

z M

r М0

О

r0

y

l s

x

Рис. 9.