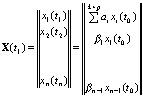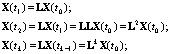Матр модели / Матричные модели популяций

Матричные модели популяций

Детализация возрастной структуры популяций приводит к классу моделей, впервые предложенных Лесли, (1945, 1948). Пусть ресурсы питания не ограничены. Размножение происходит в определенные моменты времени Пусть популяция содержит n возрастных групп. Тогда в каждый фиксированный момент времени (например, ) популяцию можно охарактеризовать вектор-столбцом

(3.18)

Вектор X(t1), характеризующий популяцию в следующий момент времени, например, через год, связан с вектором X(t0) через матрицу перехода L:

(3.19)

Установим вид этой матрицы. Из всех возрастных групп выделим те, которые производят потомство. Пусть их номера будут k, k+1 ,..., k+p. Предположим, что за единичный промежуток времени особи i-й группы переходят в группу i+1, от групп k, k+1,..., k+p появляется потомство, а часть особей от каждой группы погибает. Потомство, которое появилось за единицу времени от всех групп, поступает в группу 1.

(3.20)

Вторая компонента получается с учетом двух процессов. Первый - переход особей, находившихся в момент в первой группе, во вторую. Второй процесс - возможная гибель части из этих особей. Поэтому вторая компонента x2 (t1) равна не всей численности x1(t0), а только некоторой ее части

,

Аналогично получаются третья компонента и все остальные. Предположим, что все особи, находившиеся в момент t0 в последней возрастной группе к моменту t1 погибнут. Поэтому последняя компонента вектора X (t1) составляется лишь из тех особей, которые перешли из предыдущей возрастной группы.

Коэффициенты для каждой группы имеют следующий смысл: a - коэффициент рождаемости, b - коэффициент выживания. Вектор численностей возрастных групп в момент времени t1 представим в виде:

(3.21)

Вектор X(t1) получается умножением вектора X(t0) на матрицу

(3.22)

По диагонали матрицы стоят нули, под диагональными элементами коэффициенты выживания b, на первой строке стоят члены, характеризующие число особей, родившихся от соответствующих групп. Все остальные элементы матрицы равны нулю.

(3.23)

Таким образом, зная структуру матрицы L и начальное состояние популяции - вектор-столбец X(t0), - можно прогнозировать состояние популяции в любой наперед заданный момент времени. Главное собственное число матрицы L дает скорость, с которой размножается популяция, когда ее возрастная структура стабилизировалась.

Пример популяции из трех возрастных групп (Уильямсон, 1967)

Пусть возрастная динамика популяции характеризуется матрицей:

Такая запись означает, что исходная популяция состоит из одной самки старшего возраста (вектор столбец в правой части уравнения). Каждое животное старшего возраста, прежде чем умереть, успевает произвести в среднем 12 потомков, каждое животное среднего возраста, прежде чем умереть или перейти в следующий возрастной класс (вероятности этих событий одинаковы) производит в среднем 9 потомков. Молодые животные не производят потомства и с вероятностью 1/3 попадают в среднюю возрастную группу. По прошествии одного временного интервала в популяции будет уже 12 самок младшего возраста:

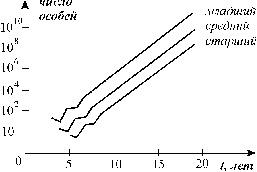
Рис. 3.18. Численность самок старшего, среднего и младшего возраста в зависимости от времени для первых 20 временных интервалов (Джефферс, 1981)

Далее процедуру следует повторять на каждом шаге. Из графика видно, что до некоторого момента времени (" t10), наблюдаются колебания численности, после чего количество самок всех трех возрастов экспоненциально возрастает, причем со-отношение между ними остается постоянным. Главное собственное число l1 при этом равно 2, т.е. размер популяции за каждый временной шаг удваивается.

Рис. 3.19. Динамика численности ценопопуляции овсеца Htlictotrichon S. Для различных возрастных групп; а - проростки, прегенеративные и генеративные особи, б - субсенильные особи, в - сенильные особи. 1 - эмпирические данные, 2 - прогноз по модели Лесли. (Розенберг, 1984).

Наклон графика равен ln l1 - собственной скорости естественного прироста. Соответствующий главному собственному числу собственный вектор отражает устойчивую структуру популяции и в нашем случае равен

Этот пример страдает тем же недостатком, что и модель Мальтуса экспоненциального роста: мы допускаем, что популяция может неограниченно расти. Более реалистическая модель должна учитывать, что все элементы матрицы L являются некоторыми функциями размера популяции.

Модели с применениями матриц Лесли для крупных возрастных групп могут дать описание колебательных изменений численности популяции. Пример такой модели ? описание динамики популяции овсеца Шелли ? мелкодерновинного злака северных луговых степей (Розенберг, 1984). Модель позволила описать наблюдаемые в природе явления - старение овсеца и колебания распределений по возрастному спектру в течение ряда лет (рис. 3.19).