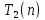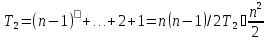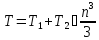Билет № 1.
1). Источники и классификация погрешностей численного решения математических задач. Неустранимая погрешность, погрешность метода, вычислительная погрешность.
2). Формулировка задачи решения систем линейных алгебраических уравнений, источники ее появления,
Причины возникновения:
Существуют типы погрешностей:
Неустранимая погрешность разделяется на две части: а) неустранимой погрешностью называют лишь погрешность, являющуюся следствием неточности задания числовых данных, входящих в математическое описание задачи б) погрешность, являющуюся следствием несоотвествия математического описания задачи реальности, называют, соотвественно погрешностью математической модели
Общая погрешность – суммарная погрешность Нат. < цел <Рац( бесконеч. периодич. Дробь) <Иррац (бесконеч. непериодич. Дробь Рац и Иррац – вещественные (действии) Комплексные числа – пара вещественных |
A(mxn) – матрица Однородная система – если вектор свободных членов равен нулевому вектору (если правая часть нулевая)
=
неопределенная. Бесчисленноемн-во решений
2
решения
=
переопределенная.несовместная
Смысл решения системы – переход от одного базиса к другому. Методы решения делят на три группы 1)прямые
методы
2)Итерационные
методы
3)методы
типа Монте-Карло ( |
Билет № 2.
1). Формы представления чисел в компьютере. Абсолютная и относительная погрешности, оценки погрешностей.
2). Метод Гаусса (схема единственного деления) решения систем линейных алгебраических уравнений. Трудоемкость и рабочее поле метода.
|
Комплексные числа представляют в виде пары вещественных чисел. Формы представления чисел в компьютере. В компьютере числа представляются
Представление чисел с фиксированной точкой: все числа в ЭВМ имеют модуль, меньший 1; число знаков после запятой фиксировано. Один байт отводится на знак числа, фиксированное число байтов отводится на целую часть и фиксированное число – на дробную часть. a = ± an , an-1 … a0 а-1 а-2 … а-m где ai – разряды, (anan-1 … a0) – целые, (а-1 а-2 … а-m) – дроби Дело в том, что в позиционной системе счисления смысл каждого разряда зависит от его позиции в этой записи. а = ± an рn + … + a1 p + a0 p0 + a-1 p-1 + … + ampm, где р – целое, основание системы счисления, ai –целые натуральные числа, такие что(0 ≤ ai<p) При использовании чисел с фиксированной точкой может возникнуть переполнение. В таком случае можно увеличить разрядность, но вырастут время обработки и занимаемая память. Представление чисел с плавающей точкой: числа представляются в виде мантиссы и порядка а = М рs, где М – мантисса (множитель, содержащий все цифры числа), p – основание системы счисления, s – порядок числа (целое число). Причем (р-1 ≤│M│<1), то есть мантисса должна быть правильной дробью, у которой первая цифра после запятой отлична от нуля. Выводы:
Абсолютная и относительная погрешности Если a - точное значение некоторой величины, а а*- известное приближение к нему (значение с погрешностью), то Δа =│а– а*│ - абсолютная погрешность, а = а* + Δа δ(а) = Δа / (│а│) = (│а – а*│) / │а│ - относительная погрешность, а = а* · (1 ± δ(а)) Оценки погрешностей
│а1 - а│≥│а2 - а│=>a= а2 │а1 - а│<│а2 - а│=>a= а1
Δа ≤ ½ (а2 - а1) = ½ ·10-t δ(а) = ½ 101-t где t – количество использованных разрядов |
|
2) Метод Гаусса (схема единственного деления) решения систем линейных алгебраических уравнений. Трудоемкость и рабочее поле метода.
На
iом
шагевыбираем элемент aii
.Принимаем j
= i.Обзовем
его ведущим. Делим строку (вместе с
iым
элементом столбца свободных членов)с
номером i
на этот элемент. Умножаем строку
(вместе с iым
элементом столбца свободных членов)с
номером i
на ai+ji.И
вычитаем из i
ой(преобразованной умножением)
строки,строку с номером i+j.Строку
с номером i+j
заменяем на получившуюся строку,строка
с номером i
остается неизменной.J
увеличиваем на 1.и так продолжаем до
тех пор пока j≠n.Как
только j=n
,делаем последнее преобразование,
выходим из цикла и увеличиваем i
на 1 .и так до тех пор пока i≠n
Трудоемкость и рабочее поле метода Рабочее
поле:
Трудоемкость метода Прямой
ход
Обратный
ход
Достоинства : простота, низкая трудоемкость вычислений Недостатки не универсальность(очередной ведущий элемент может оказаться 0),относительно невысокая точность вычисления, не запоминается информация о преобразовании правой части системы |


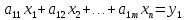
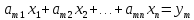
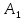
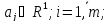
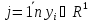

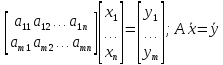

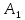
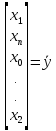

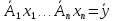
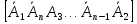








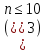
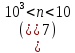
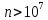 сотни алгоритмов. Зависит от
особенностей С.У.)
сотни алгоритмов. Зависит от
особенностей С.У.)

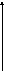
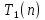
 ячеек памяти
ячеек памяти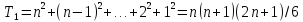 [ВМО]
[ВМО]