Vych_mat / Vych_mat / шпоры / 22-Билет(1,2)шшш

Билет № 22.

1). Метод Зейделя решения систем линейных алгебраических уравнений.

Запись итерационного стационарного процесса в канонической форме. Рассмотрим произвольную квадратную матрицу:

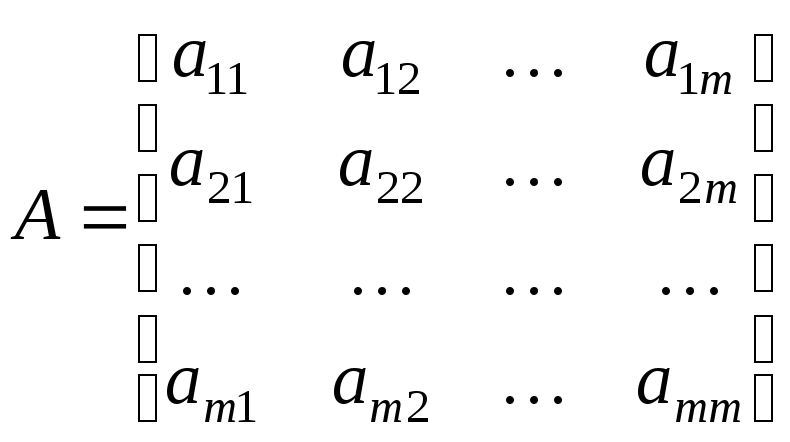
Разложим её на сумму трех матриц , где - диагональная часть матрицы , которая содержит элементы , стоящие на главной диагонали; - нижняя треугольная матрица, - верхняя треугольная матрица.

В классическом методе Зейделя, записанном в канонической форме, полагают

В результате формула принимает вид:

,

или

(*)

Перейдем от векторной формы записи рекуррентной формулы (*) к построчной:

Эти уравнения позволяют последовательно рассчитать компоненты вектора - ой итерации подобно тому, как это делалось во время обратного хода в методе Гаусса:

, .

Формула предполагает, что , . Если матрица удовлетворяет условиям теоремы Самарского: , то, все ее диагональные элементы должны быть строго положительными и, тем самым, не могут обращаться в ноль.

Алгоритм в методе Зейделя прост и удобен для вычислений. Он не требует никаких действий с матрицей . Ранее вычисленные на текущей итерации компоненты сразу же участвуют в расчетах наряду с компонентами и, таким образом, не требуют дополнительного резерва памяти, что существенно при решении больших систем.

Сходимость метода Зейделя в случае, когда матрица удовлетворяет условию теоремы Самарского, т.е. является самосопряженной и положительно определенной. Метод Зейделя сходится для любой системы , в которой матрица обладает свойством диагонального преобладания.

В методе Зейделя при вычислении (k+1)-го приближения неизвестных х₁, х_2,..., х_i-1 вычисления осущест­вляются следующим образом. Выбираем произвольно начальные приближения корней х₁⁽⁰⁾, х₂⁽⁰⁾_,..., х_n ⁽⁰⁾и подставляем в первое уравнение системы

(1):

х₁⁽¹⁾ = ₁ + ₁₁х₁⁽⁰⁾ + ₁₂х₂⁽⁰⁾ + … + _1nх_n⁽⁰⁾

полученное первое приближение х₁⁽¹⁾ подставляем во второе уравнение сис­темы (1):

х₂⁽¹⁾ = ₂ + ₂₁х₁⁽⁰⁾ + ₂₂х₂⁽⁰⁾ + … + _2nх_n⁽⁰⁾

Полученные первые приближения х₁⁽¹⁾ и х₂⁽¹⁾ подставляем в третье урав­нение системы (1):

Х₃⁽¹⁾ = ₃ + ₃₁х₁⁽⁰⁾ + ₃₂х₂⁽⁰⁾ + … + _3nх_n⁽⁰⁾

и т.д.

Наконец,

Х_n⁽¹⁾ = _n + _n1х₁⁽⁰⁾ + _n2х₂⁽⁰⁾ + … + _nn-1х_n-1⁽¹⁾ + _nnх_n⁽⁰⁾ Аналогично строим вторые, третьи т.д. итерации. Таким образом, пред­полагая, что k-e приближение корней х₁^(k) известны, по методу Зейделя строим (k+l)-e приближение по следующим формулам:

…

где k= 0, 1, 2, ..., n. Объясним откуда они появляются. Зейдель рассмотрел Метод простых итераций: x^(k+1) = x^(k) + 

Зейдель предложил разбить = В + С на сумму двух матриц. Тогда итерационная формула Метода простых итераций примет вид: x^(k+1) = Cx^(k) + 

Переносим слагаемое x^(k) в левую часть: x^(k+1) - x^(k) = Cx^(k) + 

Зейдель предложил поменять индекс k на индекс k + 1.

x^(k+1) - x^(k+1) = Cx^(k) + 

Тогда получилось соотношение: (E – B)x^(k+1) = Cx^(k) + 

Окончательно имеем:

x^(k+1) = (E – B)^(-1)Cx^(k) + (E – B)^(-1)

_zeidel = (E – B)^(-1)C

_zeidel = (E – B)^(-1)

Откуда следуют формулы приведенные выше. Преимущество метода Зейделя заключается в том, что области сходимости не совпадают, так как м. Зейделя может сходиться там, где МПИ расходиться. Число ите­раций м. Зейделя, меньше так как данные лучше подготовлены (). Скорость сходимости в м. Зейделя такая же как и в МПИ (не хуже).

Сходимость метода Зейделя

В=D+T_H; =1; A=T_H+D+Т_B

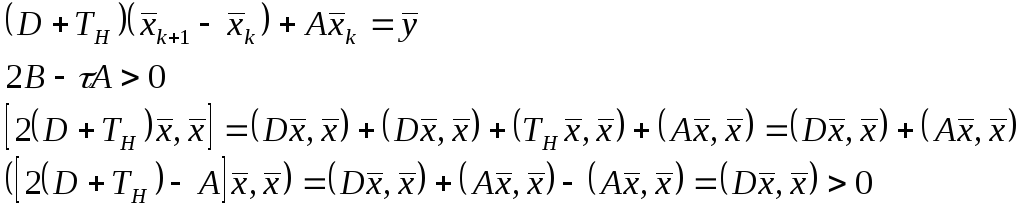
Матрица будет положительно определена, если диагональные элементы будут положительны.

Требования к выбору 

• Сходимость стационарной двухслойной схемы

• Наиболее быстрая сходимость

Требования к матрице В

Матрица-В не должна быть матрицей общего вида. Она должна быть легко обратимой, чтобы трудоемкость не превышала n² (диагональной, треугольной, их комбинацией).

Точность = kn², где (k<<n) и k - количество итераций

2). Оценка погрешностей выполнения арифметических операций с множеством чисел.

Выполнение операций над m числами

Ведем обозначения (ab) = (ab)(1+ε), где  => +, -, *, /

- произведение чисел

y₀ = 1; y_i = x_i·y_i-1;

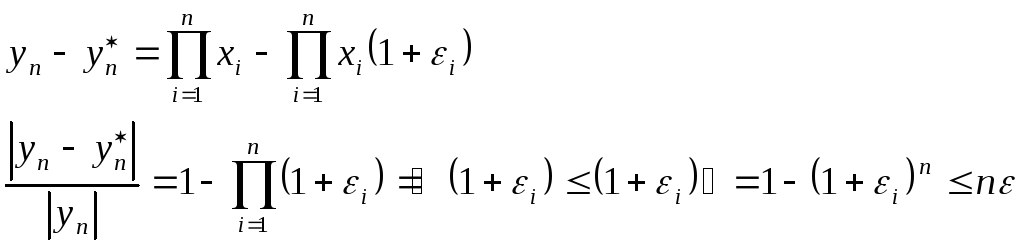
пренебрегаем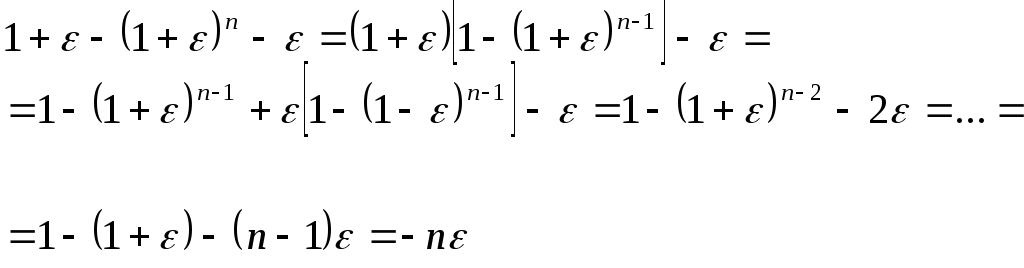

Для сложения: n²ε

В заключение:

1. Математический анализ и линейная алгебра – это абстрактные модели для задач вычислительной математики (все операции не ассоциативны)

2. Программировать оценку погрешности нереально из-за сложности и увеличения затрат. Поэтому используют оценку сверху, на практике данную задачу решают изменением входных параметров итд.