Vych_mat / Vych_mat / Экз / 14-Билет(1,2)

Билет 14

1). Нормализованные процессы разложения и их использование для определения ранга матрицы. Метод квадратного корня (случай симметричной матрицы) с20.

Минор матрицы

  А - прямоугольная матрица размеров m*n, k - любое целое положительное число, не превышающее min(m,n). Выбираем в матрице произвольные k строк и k столбцов. Элементы, стоящие на пересечении этих строк и столбцов образуют квадратную матрицу порядка k. Определитель полученной матрицы называется минором k-го порядка матрицы А.

Ранг матрицы Рангом матрицы называется наивысший порядок отличного от нуля минора этой матрицы.

метод квадратных корней

Рассмотрим систему линейных алгебраических уравнений Ax =Y. Где А=А^т – матрица А является симметричной.

Если квадратная матрица А является симметричной, то она допускает разложение

А=S ^тS, где S- верхняя треугольная матрица

Доказательство можно провести конструктивным путем, а именно нужно написать столько уравнений сколько коэффициентов в матрице

S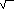₁₁ S ₁₁ = A₁₁; S₁₁= A₁;

S₁₁ S ₁₂ = A₁₂; S₁₂= A₁₂ /S₁₁;

S₁₂ S ₂₂ +S₂₂ *0= A₂₁; A₂₁ =A₁₂; в силу симметричности матрицы

Трудоемкость 1/6* n³ (в 2 раза меньше, чем в методе Гаусса)

Если матрица является положительно определенной, то все подкоренные выражения положительны

2. Постановка задачи построения интерполяционного многочлена. Кусочно-линейная интерполяция

Интерполяционный многочлен

Пусть функция у =f(x) задана таблицей своих значений:y_i=f(x_i), i=0,1,...,n,.

Многочлен называется интерполяционным для функции f(x), если его значения в точках , совпадают со значениями функции, то есть выполнены равенства: , .

Кусочно-линейная интерполяция.

При решении ряда задач требуется восстановить функцию y=f(x) для произвольного значения x на отрезке [a,b], если известны ее значения в некотором конечном числе точек этого отрезка. Кроме того, функция y=f(x) может быть задана формулой, вычисление значений которой очень трудоемко. Данная задача решается путем интерполяции.

Нахождение функции-интерполянты F(x),где F(x_i)=f_i, называют интерполяцией, а точки x₀, x₁,... , x_N - узлами интерполяции. Величины h_i=x_i-x_i-1, - называют шагами табличной функции.

Простейшим видом интерполяции является кусочно-линейная интерполяция. Она состоит в том, что заданные точки , соединяются прямолинейными отрезками, и функция f(x) приближается полученной ломаной.

Поскольку имеется N интервалов (x_i-1 , x_i), то для каждого их них в качестве уравнения интерполянты используется уравнения прямой, проходящей через две точки. В частности, для i-го интервала можно написать уравнение прямой, проходящей через точки (x_i-1 , f_i-1) и (x_i , f_i), в виде

(y-f[i-1])/(f[i]-f[i-1])=(x-x[i-1])/(x[i]-x[i-1])

Отсюда

y = a_ix + b_i  F(x), x  (x_i-1, x_i) (1)

Следовательно, при использовании кусочно-линейной интерполяции сначала нужно определить номер i интервала, в который попадает значение аргумента x, затем подставить x и i в формулу (1) и найти приближенное значение функции в точке x.