Vych_mat / Vych_mat / Экз / 12-Билет(1,2)

1. Билет № 12.

1). Ортогональные матрицы вращения (преобразования Гивенса), их использование для реализации QR-разложения.

Пусть i и j — некоторые целые индексы, такие что l ≤ i < j ≤ n,a θ — некоторое вещественное число. Рассмотрим следующую матри­цу размерности n:

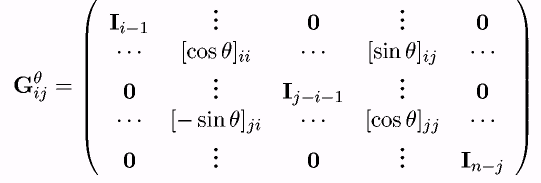
(такая матрица отличается от единичной лишь тем, что на пересече­ниях ее (i, j) строк и столбцов расставлены величины cosθ и sinθ).

Проверкой условия: если определяющая линейный оператор матрица Q удовлетворяет соотноше­нию Q^TQ = Е = I, (то есть ее обратная матрица совпадает с транспонированной) легко можно убедиться, что определяемый матрицей оператор является ортогональным.

Пусть имеется некоторый вектор х  Rⁿ и его образ х' = х. Очевидно, что они отличаются лишь i-ым и j-ым компонентами, для которых справедливо соотношение

(1)

На практике обычно возникает задача нахождения такого враще­ния, которое обнуляло бы один из компонентов х_i, или . Обозна­чим для краткости с = cosθ и s = sinθ. Если требуется обнулить x_j, то согласно (1) нужно найти такие c и s, чтобы выполнялось cx_j — sx_i = 0. Добавив к этому уравнению связывающее c и s основное тригонометрическое тождество, получим систему из двух уравнений с двумя неизвестными:

имеющую решение

Для хранения матриц вращения достаточно двух це­лых (i, j) и двух вещественных (s, с) чисел; процедура матрично-векторного умножения при этом выполняется согласно формулам (1).

Свойства:

• произведение ортогональных матриц также является ортогональной матрицей;

• матрица, обратная к ортогональной, также ортогональна.

• (Q₁Q₂)Q₂^-1Q₁^-1 = E

• Q₁Q₂ · Q₂^TQ₁^T = E

• (Q₁Q₂)(Q₁Q₂)^T = E

Замечание: чем больше , тем точнее результат деления, тем точнее оценка матрицы

Если cosθ=1 и sinθ=0, то ортогональная матрица становится единичной.

Трудоемкость метода = kn³, где k<1 (зависит от конкретной реализации ≈ n³). Метод Гивенса основан на преобразовании подобия. Алго­ритм построен таким образом, что вновь образованные нулевые элементы при всех последующих преобразованиях сохраняются. Его единственный недоста­ток состоит в том, что симметричная матрица приводится не к диагональному, а к трехдиагональному виду.

В случае матрицы размерности п х п метод Гивенса требует п — 2 основных шагов, на каждом из которых выполняется ряд преобразований, число которых зависит от числа нулей, кото­рое хотят получить в данном столбце или строке. На k -м шаге обращают в нули элементы, стоящие вне трех диагоналей k-й строки и k -го столбца, сохраняя в то же время нулевые элементы, полученные на предыдущих шагах. Таким образом, перед нача­лом k -го шага преобразованная матрица является трехдиа­гональной, если ограничиться рассмотрением ее первых k — 1 строк и столбцов. По мере преобразований симметричная матри­ца размерности 5х5 приобретает следующие формы:

	*	*	*	*	*
	*	*	*	*	*
A0=	*	*	*	*	*	исходная матрица,
	*	*	*	*	*
	*	*	*	*	*

	*	*	0	0	0
	*	*	*	*	*
A1=	0	*	*	*	*	после 1 основн шага,
	0	*	*	*	*	состоящего из 3 преобр.
	0	*	*	*	*

	*	*	0	0	0
	*	*	*	0	0
A2=	0	*	*	*	*	после 2 основн шага,
	0	0	*	*	*	состоящего из 2 преобр
	0	0	*	*	*

	*	*	0	0	0
	*	*	*	0	0	после 3 основн шага,
A3=	0	*	*	*	0	Сост. из одного преобр.
	0	0	*	*	*	Теперь матр име­ет 3диаг вид.
	0	0	0	*	*

На каждом основном шаге изменяются лишь те элементы мат­рицы а_ij, которые расположены в ее правой нижней (заштрихо­ванной) части. Ясно, что на каждой следующей стадии вы­полняется меньшее число преобразований, чем на предыдущей. Всего для приведения матрицы к трехдиагональному виду тре­буется выполнить (n² — Зп + 2)/2 преобразований.

При выполнении одного шага преобразований можно обратить в нуль сразу все элементы целой строки и столбца, стоящие вне трех диагоналей матрицы.

2). Решение частичной проблемы собственных значений. Степенной метод и его модификации.

Решение частичной проблемы собственных значений сводится к поиску нескольких собственных значений (наибольших, наименьших)

При степенном методе определяется одно наибольшее собственное значение

Степенной метод

А – λЕ

λ₁, … λ_n – собственные значения

,

,

- для i-того элемента

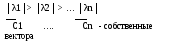
Рассмотрим отношение:

так как │λ₁│это max значение, то с ростом k вес значения в скобках будет стремиться к нулю, поэтому через определенное число итераций получим

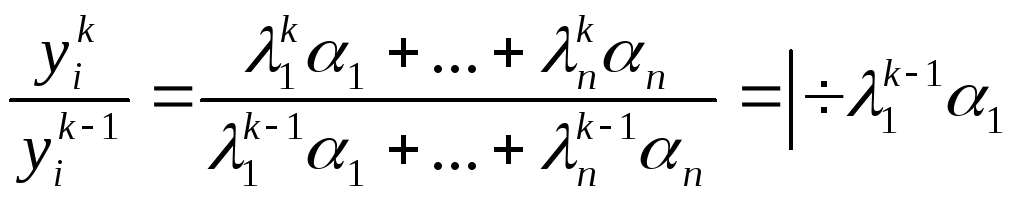
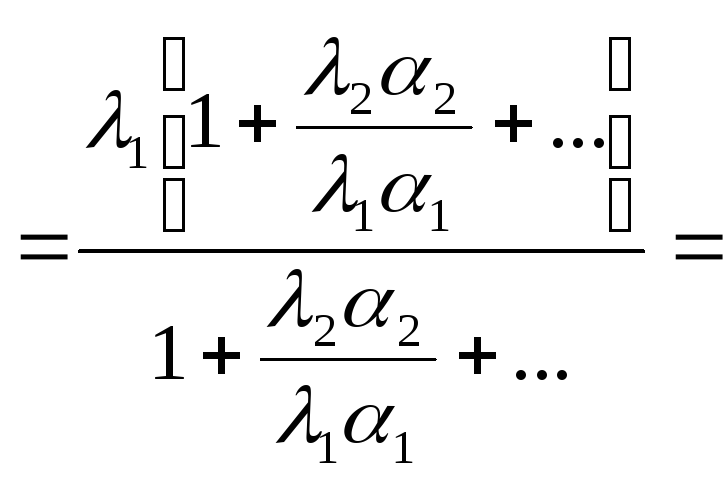
Могут возникнуть сложности, если есть несколько равных собственных значений, поэтому существуют различные модификации степенного метода для решения задачи в любом из случаев

Оценка погрешности:

Если матрица плохо обусловленная, то погрешность задания ее коэффициентов сильно влияет на результат

Существуют специальные алгоритмы, использующие разреженные матрицы для вычисления собственных значений