Vych_mat / Vych_mat / Экз / 2-Билет (1,2)

Билет № 2.

1). Формы представления чисел в компьютере. Абсолютная и относительная погрешности, оценки погрешностей.

Современные ЭВМ оперируют с числами, представленными в одной из форм: с фиксированной и плавающей запятой

Рассмотрим каждую из них:

Числа с фиксированной запятой:

a=a _n , a _n-1…a ₀ , a _–1a _-2…a _-m

целые дробые

где a _i – разряды

используется позиционная система исчисления , где значение каждого разряда зависит от позиции

a=a _n pⁿ+ a _n-1 p^n-1+…+a ₀ p+ a _–1 p^-1+ a _–2 p^-2…a _–m p^-m

где p-основание системы исчисления

a_i- натуральное число, принадлежащее множеству {0,1…p-1}

в компьютере числа с фиксированной запятой выглядят:

F_{r,t t}

r- длина

t-число разрядов под дробную чать

если m- основание с/и

тогда максимальное число m^r-1 и при нехватке разрядов возможна ситуация переполнения, а для операции деления возможна ситуация, когда останется тока целая часть или так часть остатка, которая вмещается

Числа с плавающей запятой

a=Mp^s

M-мантисса

p-основание системы

s-порядок числа

мантисса должна быть строго меньше 1 или больше или рана min числу 0.1 равному p^-1 (0.1M<1)

максимальным здесь будет число 2ⁿ-1

n-число разрядов

по умолчанию в компьютере за основание берется 2, тогда число будет выглядеть как:

мантисса*2^{порядок}

здесь возможны 2 варианта ошибок: потеря значимости –выводится ноль (если пытаются отобразить слишком точное число) или аварийное завершение программы при задании оч. большого или оч. маленького числа

Погрешности:

M₀₌10^-8 машинный ноль- самое маленькое число представляемое на машине

M_ =M_o^-1 машинная бесконечность

Погрешность в числе с фиксированном кол-вом определяется:

1) количеством отбрасываемых разрядов

пример:

F_2,1

a1=2,1

a2=2,2

a=2,18

a*=2,1 (отбрасывание восьмерки)

a=-0.08

2)округлением

|a1-a|>=|a2-a| -> a=a2

|a1-a|<|a2-a| -> a=a1

а принадлежит (a1, a2)- диапазон числа a

a  ½ (a2-a1)= ½ 10^-t

Погрешность в числе с плавающей запятой определяется формулой:

(a)= ½ 10^k-t = ½ 10 ^1-t

M* 10^k

2). Метод Гаусса (схема единственного деления) решения систем линейных алгебраических уравнений. Трудоемкость и рабочее поле метода.

Д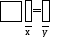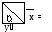ве системы называются эквивалентными, если все решения одной системы являются решениями второй и наоборот.

Условие задачи: (1) А = => (2) А = у

Суть метода состоит в том, что путем элементарных преобразований из всех уравнений системы, кроме первого, исключаем неизвестное   x₁,   далее из всех уравнений, кроме первого и второго, исключаем неизвестное   x₂,  и т.д. (То есть, матрица приводится к треугольному виду, верхняя треугольная матрица.). Причем главный элемент выбирается максимальным! На практике принято все эти действия проводить не над уравнениями системы, а над строками расширенной матрицы.

В основе метода Гаусса – элементарные операции:

1. перестановка уравнений местами

2. умножение какого-либо уравнения на число ≠ 0

3. замена i – того уравнения на сумму i – того и j – того (возможно, умноженного на число)

Критериями являются – ранг матрицы (= n) или А ≠ 0

А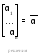₁ (х₁₁, х₁₂, … х_1n) = y

………………………..

A_m (x_m1, x_m2, … x_mn) = y_n

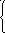
f₁ (α_{1, …} α_n) = y₁

Процесс решения системы уравнений разбивается на 2 этапа:

1. Прямой ход метода Гаусса – преобразование системы (1) в систему (2). В результате элементарных преобразований получается матрица, эквивалентная исходной, т.е. матрица, имеющая такой же ранг. На ее основе составляется система, эквивалентная исходной, но более простая в решении и анализе, так как в последнем уравнении останется только одно неизвестное, в предпоследнем два и т.д. Отметим, что параллельно при этом решается вопрос о совместности системы и количестве решений (единственное или бесконечное множество.)

2. Обратный ход метода Гаусса – решение системы. Из последнего уравнения находим единственное входящее в него неизвестное, подставляем полученное значение в предпоследнее уравнение и находим второе неизвестное и т.д. пока не дойдем до первого уравнения, в котором уже найдены все неизвестные, кроме одного. Таким образом получим совокупность значений неизвестных, образующих решение системы.

Характеристики метода:

1. Рабочее поле: n² + 2n ячеек

2. Трудоемкость: D-трудоемкость всего метода(прямой и обратный ход)

D1-количество мультипликативных операций

D2- затраченное на правую часть

D3- обратный ход

D1=n³/3

D2=D3=1/2n²

D=D1+D2+D3

3. Точность метода = kn³, где k - количество итераций

a₁₁ … a_1n y₁ 1 a₁₂’ … a_1n’ y₁

… … … … => a₁₁ a₂₂ … a_2n y₂ =>

… … … … … … … … …

a_m1 … a_mn y_n a_m1 a_m2 … a_mn y_n

1 a₁₂’ … a_1n y₁’ 1

=> * (-a₂₁) 0 a₂₂ … a_2n y₂ => * (-a₃₁) … => x =

… … … … … 0 1

a_m1 a_mn … a_mn y_n

А у

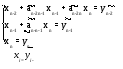
При решении СЛАУ по методу Гаусса мы сталкиваемся с

1. решением частичной проблемы собственных значений

2. решением полной системы собственных значений

Достоинства метода:

• Метод чрезвычайно прост

• Один из самых быстрых методов для матриц общего вида

Недостатки метода

• Метод не универсален (в процессе прямого хода при делении на ведущий элемент, он может оказаться равным нулю)

• Относительно небольшая точность

• В методе нет памяти