Vych_mat / Vych_mat / Экз / 9-Билет(1,2)!

билет 9

1.Итерационное уточнение решений системы линейных алгебраических уравнений

В реальном компьютере вследствие конечности разрядной сетки арифметические операции могут быть не точными. Поэтому найденный любым прямым методом вектор x⁽⁰⁾ не будет, вообще говоря, решением системы

(A x⁽⁰⁾ ≠0) , и невязка окажется отличной от нуля:

d⁽⁰⁾ =b-Ax⁽⁰⁾ ≠θ

Попробуем подобрать такой вектор ∆x ("добавку" к x⁽⁰⁾), чтобы выполнилось равенство

А(x⁽⁰⁾ + ∆х) = b. Искомый вектор ∆x⁽⁰⁾ найдем, решая систему

A∆x =b –Ax⁽⁰⁾ =d⁽⁰⁾с той же матрицей, тем же прямым методом.

Понятно, что из-за неточности машинной арифметики полученный вектор x⁽¹⁾ =x⁽⁰⁾ +∆x⁽⁰⁾ также не будет, вообще говоря, решением системы (Ах⁽¹⁾ ≠b). Находим новую невязку и т.д.

Мы построили итерационный процесс

d^(k) =b-Ax^(k) ,x^(k+1) =x^(k) +∆x^(k)

где ∆x^(k) - полученное прямым методом "решение"системы A∆x=d^{( k)}

Замечания. 1. Вычисление невязок должно выполняться в арифметике повышенной точности, иначе ите­рации не обеспечат уточнения.

2. Если прямой метод основан на какой-нибудь факторизации матрицы коэффициентов системы, то эту факторизацию - самую трудоемкую часть работы - следует выполнить один раз, полученные сомножители хранить и использовать на каждом шаге итерации.

2. Подробное исследование описанного процесса уточнения решения показало, что для не очень плохо обусловленных систем он сходится чрезвычайно быстро: три-четыре итерации обеспечивают получение решения с машинной точностью. Отсутствие же сходимости свидетельствует об очень большом числе обусловленности, что обычно означает, что эту систему решать не следует.

2). Методы вычисления собственных значений, основанные на идее интерполяции (линейная и квадратичная интерполяция).

Интерполяция- восстановление значения функции в промежуточной точке по известным ее значениям в соседних точках

Аппроксимация-нахождение наиболее точного приближения.

Интерполяция – один из способов аппроксимации данных. В простейшем (одномерном) случае

задача интерполяции состоит в следующем: заданы точки (x_i, y_i), и требуется найти функцию (x), которая проходит через эти точки

т.е. (x_i)= y_i , (1)                  

Точки (x_i, y_i) называют узлами интерполяции, а функцию (x) – интерполирующей функцией.. Рассмотрим задачу линейной интерполяции. При этом интерполирующая функция имеет следующий вид:

,      (2)

где ₀(x), ₁(x), … , _m(x) – базисные функции.

Используя условие (1) и выражение (2), получаем систему уравнений

        (3)

Единственное решение системы (3) существует при двух условиях:

1. число точек (x_i, y_i), 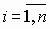равно числу коэффициентов С_k, ;

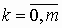2. система уравнений (3) должна быть невырожденной, т.е. определитель системы .

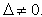Таким образом, если выполняются вышеуказанные условия, то через точки (x_i, y_i) проходит единственная функция .

Выражение (1) определяет поведение функции (x) только в узлах интерполяции (x_i, y_i), . Между узлами (x) может вести себя произвольным образом, сколь угодно далеко, в принципе, отклоняясь от зависимости f(x). Определить погрешность приближения можно, используя выражение для абсолютной ошибки =| f(x) – (x) |.

Ошибка полиномиальной интерполяции. Лучший способ проверить качество интерполяции – вычислить значения интерполирующей функции в большом числе точек и построить график. Квадратичная интерполяци Идея метода квадратичной интерполяции заключается в построении интерполяционного многочлена 2-й степени по трем точкам, взятым вблизи минимума. Положение минимума многочлена принимается в качестве нового приближения к искомой точке минимума функции.

Пусть f₁, f₂, f₃ - значения функции f(x) в точках x₁, x₂ и x₃, соответственно. Запишем интерполяционный многочлен в форме Лагранжа:

.Дифференцируя это выражение, получим первую производную:

.

Приравнивая производную нулю, найдем положение минимума P₂(x):

. (5)

 Обозначим через x₄ приближение к точке минимума, рассчитанное по формуле (5). Отбросим одну из прежних точек так, чтобы оставшиеся три точки (включая новую) ограничивали минимум. Повторяя шаг, найдем новое приближение с помощью квадратичной интерполяции, оставим три ближайшие к минимуму точки и т. д. Процесс заканчивают, когда длина интервала неопределенности либо относительное понижение значения функции на двух последовательных шагах становятся меньше заданной величины.

     По мере приближения к минимуму величины x₁, x₂ и x₃, входящие в формулу (5), все более сближаются (как и соответствующие значения функции). При этом непосредственное использование (5) может привести к вычислительным трудностям из-за потери точности в результате вычитания близких величин. Поэтому формулу приводят к более удобному для вычислений виду:

(5а)

     Первое слагаемое в (5а) определяет середину отрезка [x₁, x₂] и не страдает от потери точности при сближении точек. Второе слагаемое мало по сравнению с первым (числитель дроби содержит произведение трех малых разностей, тогда как знаменатель представляет собой комбинацию первых степеней этих разностей). Конечно, второе слагаемое будет найдено с увеличенной относительной погрешностью из-за потери точности, но это погрешность малой поправки к первому слагаемому, и ее влияние на конечный результат невелико.