Волновая оптика и квантовая физика_2010

она движется, то, решив это уравнение, можно найти волновую функцию и узнать состояние частицы в последующие моменты времени.

Если силовое поле, в котором движется частица, посто- янно во времени, то U не зависит от времени и волновую функ- цию можно представить в виде произведения двух функций, од- на из которых – φ – не зависит от времени t.

ψ(x,y,z,t) = j(x,y,z)× e−	i
		Et
	h		,

где Е – полная энергия частицы. Если мы подставим такую функцию в уравнение Шредингера, проведем дифференцирова- ние и сокращение, то получим уравнение

−	h2	ϕ +Uϕ = Eϕ или	2m	ϕ = 0
	2m		ϕ + (E-U ) h2		.

Это - уравнение Шредингера для стационарных состояний час- тиц, оно позволяет определить волновую функцию φ, которая зависит только от координат частицы.

8.6. Частица в потенциальной яме. Квантование энергии частицы. Туннельный эффект

Рассмотрим поведение микрочастицы в одномерной бес- конечно глубокой потенциальной «яме». Такой вид потенциала взаимодействия в природе не наблюдается (наиболее близок он к потенциалу, используемому при рассмотрении электрона в ме- талле), но из-за простоты его удобно использовать для нахожде- ния волновой функции. Такая потенциальная «яма» описывается следующими соотношениями для потенциальной энергии (рис. 8.4): в областях 1,3 для x≤0 и x≥a U = ∞ ; в области 2 для

0<x<a U = 0.

101

Рис. 8.4. График потенциала одномерной бесконечно глубокой «ямы».

Запишем стационарное уравнение Шредингера для об- ластей 1, 3 , где U = ∞:

∂2ϕ	+ (E-∞)	2m	ϕ = 0 .
∂x 2
		h2

Его единственное решение ϕ = 0. Это означает, что вероятность нахождения частицы в областях 1 и 3 равна нулю и частица туда

проникнуть не может вследствие бесконечно высоких «стен у ямы».

Для области 2 уравнение имеет вид

∂2ϕ + E 2m ϕ = 0 ,

∂x2 h2

оно имеет множество решений вида

ϕ = Asin (kx) + B sin (kx), k = E 2m . h 2

Вследствие требования непрерывности функции ϕ, она должна быть равна нулю в точках x = 0 и x = a, что следует из решения для областей 1, 3. Это будет выполняться согласно ма- тематике, если принять B = 0 и ka = πn, где n-целое число. Необ- ходимое также условие нормировки в данной задаче имеет вид

		a			πn
A	2	∫sin	2
					a	x dx = 1.
		0

102

A = 2 / a

Взяв этот интеграл, получаем и в результате имеем конечное выражение для возможных решений уравнения Шре- дингера в поставленной задаче

ϕ = 2/a sin ( πn x), n = 1, 2, 3, ... .

a

Данное решение показывает, что поведение микрочасти- цы в одномерной бесконечно глубокой потенциальной «яме» может быть различным в зависимости от значения числа n, его называют квантовым числом и оно считается номером возмож- ного состояния микрочастицы.

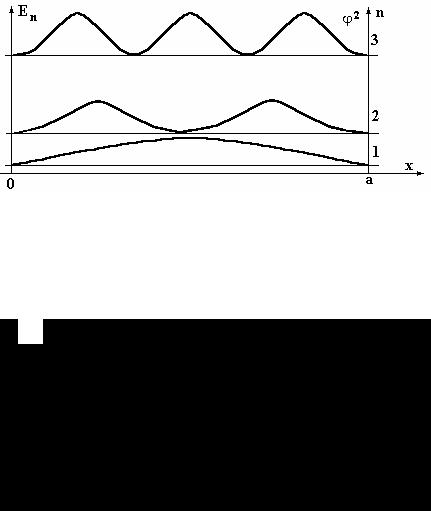
Рассмотрим графики для вероятности нахождения части- цы в разных точках «ямы» (рис. 8.5), которая определяется квадратом волновой функции.

Из рис. 8.5 видно, что во втором и в третьем состояниях микрочастица не может находиться в некоторых точках «ямы», однако она может находиться между этими точками. Кроме это-

En

Рис. 8.5. Графики вероятности нахождения частицы в бесконечно глубокой потенциальной «яме» для n = 1, 2, 3. Горизонтальные, тонкие линии показывают значения энергии состояний (энергетическая диаграмма или уровни возможных энергий системы), толстые линии показывают ϕ2.

103

го, видно, что минимальное значение полной энергии Е1, кото- рая в области 2 является кинетической энергией, не равно нулю, это означает что частица находится в непрерывном движении. Такое поведение микрочастицы существенно отличается от по- ведения макрочастицы и приводит к тому, что в квантовой ме- ханике понятие траектории не может быть использовано так же, как в классической механике.

Используя найденные соотношения ka = πn и стационар- ное уравнение Шредингера для области 2, получим выражение для полной энергии частицы

		πn 2		h	2
En	=					,
		a		2m

которое показывает, что энергия частицы в разных состояниях различна и строго определена. Других значений энергии частица иметь не может. Возможные дискретные значения называют

квантовыми уровнями энергии или энергетическими уровнями.

Подобное квантование может происходить и с другими пара- метрами микрочастиц: импульсом, моментом импульса.

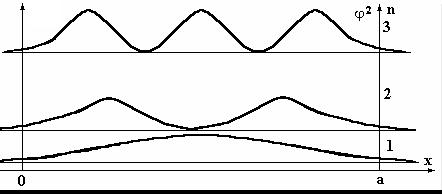
Рассмотрим более реальную ситуацию, когда частица на- ходится в одномерной потенциальной «яме» конечной глубины (в областях 1, 3 для x≤0 и x≥a имеем U = U0; в области 2 для 0>x>a имеем U = 0). Для этого случая кроме квантования энер-

гии, мы получим, что функция ϕ2 не будет равна нулю в облас- тях 1, 3 для всех состояний (рис. 8.6). На рисунке видно, что за-

висимости выходят из области 2 в первую и третью области. Это говорит о том, что частица может выйти за пределы потенци- альной «ямы» даже в случае, когда ее энергия меньше U0, чего в классической механике происходить не может. В физике эле- ментарных частиц подобное явление наблюдается при радиоак- тивном излучении и выходе альфа-частиц из ядер атомов. По- добное явление наблюдается и при рассмотрении поведения микрочастицы вблизи одномерного потенциального «барьера». Потенциальная энергия барьера U = 0 для областей 1 и 3 и U=U0

104

для области 2. Если решить уравнение Шредингера для данного случая, то можно обнаружить, что частица с энергией меньшей U0 может проходить сквозь этот «барьер».

En

Рис. 8.6. Графики вероятности нахождения частицы в по- тенциальной «яме» конечной глубины и значения энер- гии состояний для n = 1, 2, 3.

Такие явления - прохождения сквозь потенциальные барьеры частиц с малой энергией - являются чисто квантовыми и называются «туннельными эффектами». Экспериментально эти явления наблюдаются с микрочастицами в различных си- туациях: автоэлектронная эмиссия – выход электронов за преде- лы металлов, автоионизация – выход электронов из атомов и молекул под действием слабого электрического поля, когда энергии поля бывает недостаточно для вырывания электрона с точки зрения классической механики.

Рассмотрим поведение микрочастицы в силовом поле, когда потенциальная энергия зависит от координаты x в соот- ветствии с законом U = m(ω0 x)2/2. Этот случай соответствует в классической механике энергии гармонически колеблющегося тела массой m с циклической частотой ω0 (гармонический ос- циллятор). Примерно такие же колебания в мире микрочастиц происходят при движении атомов в молекуле, а также при коле-

105

баниях молекул около узлов кристаллической решетки в твер- дых телах.

В классической механике гармонический осциллятор может иметь любую произвольную полную энергию Е, а его максимальное смещение от положения равновесия (амплитуда колебаний) xo ограничено и связано с энергией соотношением Е = m(ω0 x0)2/2. В квантовой механике для анализа особенностей движения гармонического осциллятора необходимо решить уравнение Шредингера с данной потенциальной энергией

∂2ϕ				mω2			2m
				0		2
∂x	2	+	E −	2	x		h	2 ϕ = 0 .

Решение такого дифференциального уравнения в анали- тическом виде достаточно сложно, но качественные особенно- сти аналогичны предыдущим случаям. На рис. 8.7 представлены графики получаемого решения и возможные значения энергий. Возможные значения для полной энергии при решении опреде- ляются формулой

En = (n +1/ 2)hω0 , n = 1, 2, 3 ...

Из этой формулы видно, что полная энергия гармонического ос- циллятора тоже квантована, а ее минимальная величина при n = 0 отлична от нуля, так же, как и в предыдущих случаях. На- личие энергии нулевых колебаний – это чисто квантовый эф- фект, он говорит о том, даже в области нулевой потенциальной энергии у частицы имеется кинетическая энергия. Это означает, что микрочастица постоянно двигается и не может находиться в абсолютном покое.

Наличие нулевых колебаний было подтверждено в экспе- риментах по рассеиванию света в кристаллах. Согласно класси- ческой теории, при абсолютном нуле температуры колебание атомов около узлов кристаллической решетки и, соответствен- но, рассеивание света, вызываемое этими колебаниями, не про- исходит. Эксперименты показывают, что интенсивность рассе-

106

				n
		En
U(x)

Рис. 8.7. Графики вероятности нахождения гармонического осциллятора для n = 0, 1, 2. Горизонтальные, тонкие линии показывают значения энергий состояний, толстые линии по- казывают ϕ2, пунктирная – вид потенциала.

янного света при уменьшении температуры уменьшается, но не обращается в ноль при абсолютном нуле, что доказывает нали- чие нулевых колебаний.

Весь изложенный материал, указывает на необходимость использования квантово-механического описания поведения микрочастиц.

9.ФИЗИКА АТОМА

9.1.Электрон в атоме водорода. Энергетические уровни.

Квантовые числа

Квантово-механическая теория атома, построенная на уравнении Шредингера, гораздо совершеннее полу-классичеc- кой теории атома Бора, построенной на ряде постулатов.При этом она сохраняет некоторые аспекты теории Бора. Так, на- пример, согласно квантовой теории, электроны могут находить- ся в атоме только в состояниях с определенной дискретной энергией; при переходе электрона из одного состояния в другое

107

испускается (или поглощается) фотон. Но квантовая механика не просто дополняет теорию Бора, она рисует совершенно иную картину строения атома. Согласно квантовой механике, у элек- тронов не существует определенных круговых орбит, как в тео- рии Бора. В силу волновой природы, электрон «размазан» в про- странстве, т.е. может с определенной вероятностью находится в любой точке пространства.

Для атома водорода движение его единственного элек- трона можно рассматривать как движение в электрическом поле ядра. По аналогии с задачей о движении частицы в потенциаль- ной яме простой формы, здесь необходимо найти решения ста- ционарного уравнения Шредингера в трехмерном пространстве с конкретным видом потенциальной энергии, описывающем электростатическое взаимодействие электрона с ядром

U = −	q 2
		.
	4π ε0 r

При решении уравнения Шредингера в данном случае используют специальные сферические функции математической физики и сферическую систему координат, центр которой сов- падает с центром ядра атома. Если записать уравнение Шре- дингера в сферических координатах (r, α, θ), то его можно строго аналитически решить, это решение представляют в виде произведения трех функций

ϕ = Rn (r) Θlm (θ) φm (α).

Важной особенностью решения является его зависимость от трех чисел n, l, m, называемых квантовыми числами. В кван- товой механике каждому решению соответствует определенное состояние атома со своим распределением электрона вокруг яд- ра, которое задается соответствующей волновой функцией, за- висящей от трех квантовых чисел n, l, m.

108

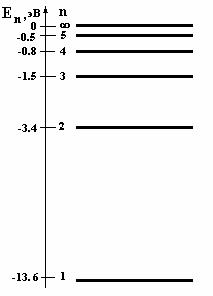
Квантовое число n называется главным квантовым чис- лом, от него зависит значение полной энергии атома водорода, при этом атом может иметь не любые значения энергии Е, а лишь некоторые Еn. Квантовое число n может принимать сле- дующий ряд значений n = 1, 2, 3, … ∞. Значения энергии Еn, ко- торые может иметь атом, называют разрешенными значениями энергии атома, а их совокупность Е1, Е2, … Е∞ представляет со- бой энергетический спектр атома. Разрешенные значения энер- гии обычно изображаются в виде горизонтальных линий, назы- ваемых энергетическими уровнями. Для атома водорода кванто- вая механика предсказывает точно такие же энергетические

уровни, что и теория Бора, т.е.
	13,6 эВ
								n
En = −			, n = 1,2,3... .			En
@		n 2
Состояние атома с наименьшей
энергией		называется		основным
(n=1), все остальные состояния –
возбужденными (рис. 9.1).
Орбитальное				квантовое
число l связано с моментом им-
пульса орбитального				движения
электрона вокруг ядра. Так как
электрон		имеет электрический
заряд, то его движение вокруг
ядра приводит к появлению маг-
нитного момента, аналогичного
магнитному моменту кругового
витка с током. Орбитальное
квантовое число l может прини-							Рис. 9.1. Схема энерге-
мать значения от 0 до n-1 и кван-						тических уровней атома
тует величину момента импуль-								водорода.
са Ll и магнитного момента μl
согласно соотношениям
				109

L =

h

= −µ

h

, l = 0, ... n −1 ,

l(l +1)

2

π

,

µ

l

Б

l(l +1)

2π

l

где μБ - постоянная, служащая единицей измерения магнитных моментов атомов и называемая магнетоном Бора. Сравнивая формулу квантования момента импульса здесь и в теории Бора, можно заметить, что они не совпадают. Более того, при l = 0 в квантовой механике возможны состояния атома с нулевым мо- ментом импульса электрона. Опыт подтверждает существование квантовых состояний атома с нулевыми орбитальными момен- тами, хотя при классическом описании движения электрона в атоме по определенной орбите атом должен всегда обладать не- нулевым моментом импульса.

Магнитное квантовое число m характеризует ориента-

цию момента импульса L и магнитного момента μ во внешнем силовом поле (например, магнитном или электрическом) и мо- жет принимать целочисленные значения от - l до + l. Согласно классической теории, магнитный момент всегда стремится по- вернуться вдоль направления магнитного поля. В квантовой ме- ханике движение электрона таково, что магнитный момент мо- жет быть направлен в нескольких, строго определенных направ- лениях в зависимости от состояния атома, т.е. он квантуется не только по величине, но и по направлению. Такое пространст- венное квантование приводит к тому, что проекции момента импульса и магнитного момента электрона на выделенное в пространстве направление могут иметь только строго опреде- ленные значения. Ориентацию магнитного момента и момента импульса задают, указывая его компоненту вдоль оси z, совпа- дающей с направлением магнитного поля. В квантовой механи- ке возможные проекции Lz и μz определяются магнитным кван- товым числом m с помощью соотношений

Lz=m h , μz = -μБ m, m = -l, -l +1, ……, l -1, l.

Так как формула квантования проекции механического момента соответствует вполне определенным направлениям ориентации

110