Лекция № 3. Фракталы

3.1. Канторово множество

Математика изобилует парадоксальными объектами. Одним из них является канторово множество. Оно описывается следующим образом. Рассмотрим единичный отрезок, показанный на рис. 3.1. Удалим из него открытую среднюю часть (1/3, 2/3) оставив два отрезка длины 1/3. Затем применим ту же самую процедуру к этим отрезкам, т.е. удалим их средние части. Продолжая процесс индуктивно до бесконечности, получим троичное канторово множество.

Рис. 3.1. Троичное канторово множество

Канторово множество можно построить не только геометрически, но и аналитически. Оно является совокупностью таких чисел из отрезка [0, 1], которые могут быть записаны в троичной системе счисления без использования цифры 1.

Доказательство. Интервал (1/3, 2/3) – это в точности множество чисел, у которых в первом разряде после запятой стоит 1 (при записи в троичной системе), т.е. которые в троичной системе не могут быть записаны в виде 0,0… или 0,2… (заметим, что 1/3 можно записать как 0,02222…, а 2/3 как 0,20000…). Соответственно средние части оставшихся отрезков – в точности те числа, для которых второй разряд после запятой должен быть равен 1, и т.д.

Троичное канторово множество обладает удивительными свойствами. Оно вполне несвязно, однако одновременно оно несчетно.

Доказательство. Сопоставляя каждой точке , () число, мы определяем отображение (функцию), потому что все двоичные разложения можно представить в таком виде. Образ канторова множества несчетен, следовательно, и само это множество несчетно. Функцияпредставлена на рис. 3.1. Она называетсяканторовой лестницей.

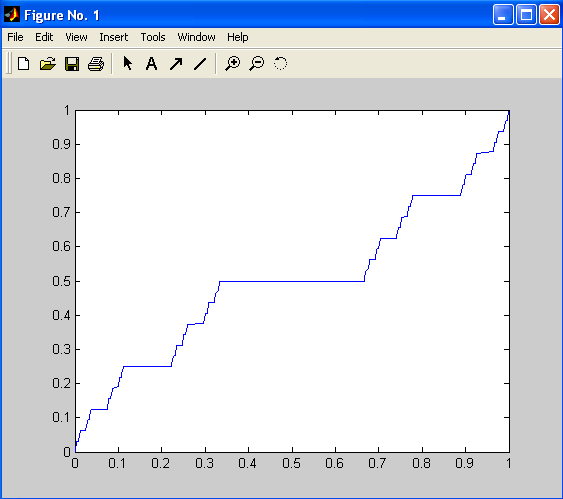
Рис. 3.2. Канторова лестница

В англоязычной литературе канторову лестницу называют «лестницей дьявола» (devil stairs). Этот термин возник из-за необычной ситуации – график этой функции полностью состоит из «ступенек», а именно горизонтальных отрезков на дополнительных интервалах, но все же разрывов эта функция не имеет – она непрерывна. Таким образом, сами ступеньки на лестнице имеются, но вот их боковые грани отсутствуют. Тем самым мы получаем удивительный пример функции с некоторыми экзотическими свойствами. Микроскопическая структура канторовой лестницы точно такая же, как и глобальная структура; она не станет более простой в любом другом уменьшенном масштабе. Линии, обладающие подобными свойствами, называются фракталами. Представленный на рис. 3.1 график канторовой лестницы был построен с использованием следующей программы MATLAB.

for k=1:1023

Sum=0;

for i=1:10

p=floor(k/(2^(10-i)));

if rem(p,2)==0

b(i)=0;

else

b(i)=1;

end

Sum=Sum+b(i)/(3^i);

end

x(k)=2*Sum;

y(k)=k/1024;

end

plot(x, y)

3.2. Ковер Серпинского и снежинка Коха

Ковер Серпинского получается из единичного квадрата удалением средней части (1/3, 2/3)*(1/3, 2/3), затем удалением из каждого квадрата (i/3, i+1/3)*(j/3, j+1/3) среднего квадрата и т.д. (рис. 3.3). Можно также начать построение равностороннего треугольника с горизонтальным основанием и разделить его на четыре конгруэнтных (идентичных) равносторонних треугольника, центральный из которых имеет горизонтальную верхнюю сторону. Затем мы удаляем этот центральный треугольник и продолжаем построение, оставляя каждый раз по три треугольника.

Рис. 3.3. Квадратный и треугольный ковры Серпинского

Трехмерный вариант ковра Серпинского (губка Серпинского или кривая Менгера) получается из заполненного единичного куба, если вырезать в его центре полый куб со стороной 1/3, а затем двадцать шесть определенным образом расположенных полых кубов со стороной 1/9 и т.д.

Снежинка Коха получается из равностороннего треугольника, если поставить на каждую его сторону равносторонний треугольник, основание которого есть средняя треть стороны, а затем продолжать этот процесс итерационно со сторонами получающегося многоугольника (рис. 3.4). Эта конструкция была предложена Хельге фон Кохом (1904 г.).

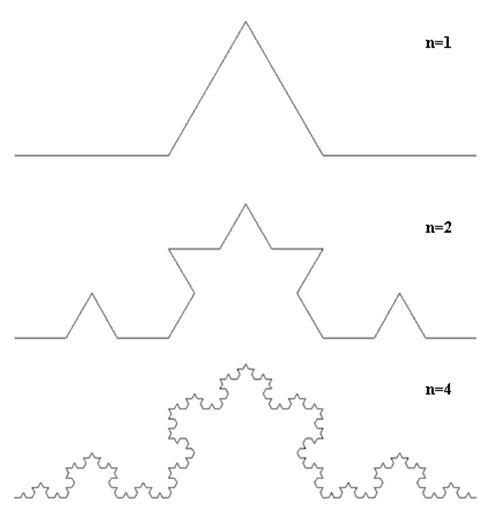
Рис. 3.4. Снежинка Коха

С математической точки зрения снежинка Коха – это линия. Однако эта линия обладает необычными свойствами. Как бы мы ни увеличивали масштаб, на этой линии всегда будут неровности. Поэтому провести касательную к такой линии невозможно. Следовательно, функция, имеющая график в виде снежинки Коха, не имеет производных.

И троичное множество Кантора, и ковер Серпинского, и снежинка Коха образуются в результате бесконечного итерационного процесса. Далее в этой главе будет показано, что такие объекты имеют дробную размерность (в отличие от гладких линий, гладких поверхностей и т.п., которые имеют целочисленные размерности). Понятие дробной размерности впервые ввел известный немецкий математик Феликс Хаусдорф (1868-1942) в начале 20 века. Поэтому описанные в данном разделе объекты называют фракталами (от англ. fractal – дробная размерность).