1.6.1.Поправка за центрировку

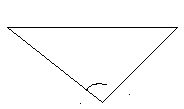
Рис. 2 Элементы центрировки и поправка в измеряемое направление за центрировку

Воспользуемся теоремой синусов и запишем (формула 7):

(7)

где С – поправка за центрировку»

S – расстояние между пунктами геодезической сети.

Формула 8.

(8)

Ввиду малости угла С можно принять , тогда для любого направления поправка (в секундах) за центрировку определяется формулой: 9

(9)

Знак поправки определяется знаком синуса угла (Ө+М):

- при (Ө+М) ≤ 180˚, С ≥ 0;

- при (Ө+М) ≥ 180˚, С ≤ 0;

Для начального направления М = 0, поэтому формула 9 принимает вид:

(10)

Поправка за редукцию

Рис. 3. Элементы редукции и поправка в измеряемое направление за редукцию

Для нахождения поправки за редукцию воспользуемся теоремой синусов, получаем следующие соотношения (формулы 11-12):

(11)

(12)

Формула для нахождения поправки (формула 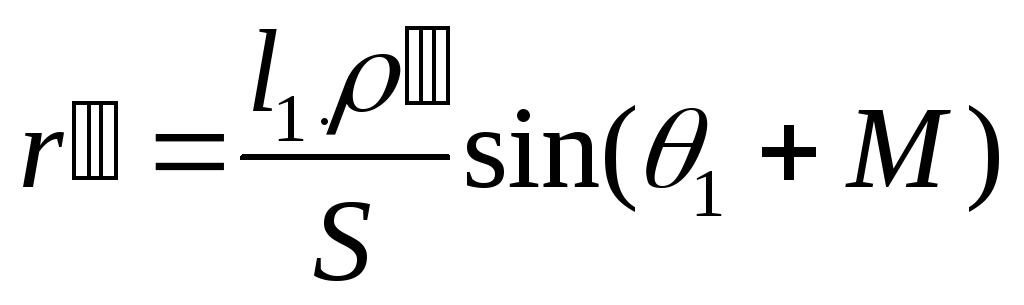13):

(13)

2. Расчетная часть

1. Выбор метода уравнивания триангуляционной сети

Триангуляционные сети по числу имеющихся исходных данных принято подразделять два вида: свободные и несвободные сети.

Сеть триангуляции, имеющая только необходимые и достаточные исходные данные, т. е один базис, координаты исходного пункта и дирекционный угол какой – либо стороны, или же имеющая вместо указанных величин координаты двух пунктов, называется свободной сетью.

Триангуляционные сети, в которых помимо необходимых имеются избыточные исходные данные, называются несвободными сетями.

Вычислительный процесс нахождения наиболее надежных значений измеренных величин при наличии избыточных измерений называется уравниванием. Окончательные значения измеренных величин характеризуют соответствующей оценкой их точности.

При наличии избыточных величин в сети появляются невязки, которые должны быть устранены в процессе уравнительных вычислений путем введения поправок в измеренные величины. В этом и заключается существо задачи уравнивания.

Однако поставленная в таком виде задача имеет множество решений. Для получения однозначного решения задачи уравнивание выполняют по методу наименьших квадратов, в соответствии с которым в измеренные величины вводят поправки V_і удовлетворяющие условию [V²] = min (для неравноточных измерений) и [рV²] = min (для неравноточных измерений). Доказано, что соблюдение указанных выше условий приводит к наилучшим оценкам для определяемых величин. В этом случае уравнительные вычисления называют строгими. Строгое уравнивание сетей связано с большим объемом вычислений, поэтому при решении некоторых специальных задач часто прибегают к различным упрощенным способом уравнивания.

При уравнивании геодезических построений используют два основных способа: параметрический и коррелатный. При коррелатном способе поправки отыскивают непосредственно к измеренным величинам, а при параметрическом к их функциям.

Существо первого способа сводится к непосредственному получению уравненных неизвестных, а второго – к вычислению неопределенных множителей – коррелат, пользуясь которыми определяют неизвестные как функции.

Параметрический и коррелатный способы, приводящие к одним и тем же результатам, относят к строгим способом уравнивания геодезических сетей, позволяющим:

1. Выполнить все геометрические условия в сети;

2. Найти наиболее надежные значения измеренных величин под условием [V²] = min или [pv²] = min соответственно для равноточных и неравноточных измерений;

3. Оценить точность результатов измерений и их функций, т.е уравненных элементов сети.