Дискретная математика - Лабораторная работа 3

Лабораторная работа №3

Произведение множеств, отношения

Цель: научиться находить произведение множеств и строить матрицы отношений

Прямое (декартовое) произведение множеств А и В– есть множество

С=А В, состоящее из упорядоченных пар (a,b), что первый элемент a

принадлежит множеству А, а второй элемент b множеству В.

С A B a,b a A,b B .

Например, пусть A={x,y} и B={1,2,3}. Тогда

А В={(x,1), (x,2), (x,3), (y,1), (y,2), (y,3)}.

Прямые произведения двух множеств можно интерпретировать графически. Для этого выберем две оси (рис.1), на первой отложим элементы множества A = {x,y,z}, а на второй элементы B={1,2,3}. Точки пересечения являются элементами А В. Именно в связи с этим представлением пары

(a,b) первый элемент называется абсциссой, а второй – ординатой.

X Y Z

Рис.1Графическая интерпретация прямого произведения Второй вариант представления А В – табличный (рис.2).

Рис.2 Табличная интерпретация прямого произведения

Отношения

Пусть заданы множества M1,M2,…,Mn. Тогда подмножество

R M1 M2 … Mn называется n-местным отношением на множествах

M1,M2,…,Mn. Многоместные отношения используются, например, в теории баз данных. Поэтому и название «реляционная» база данных происходит от relation (отношение). Говорят, что m1M1, m2M2,…, mnMn находятся в отношении R, если (m1,m2,…,mn) R. Одноместное отношение R - просто подмножество M, т.е. R M . Такое отношение называется признаком: m

обладает признаком R, если m M и R M. Свойства одноместных отношений это свойства подмножеств множества M.

Наиболее часто используются бинарные отношения. Бинарные отношения - это отношения между двумя объектами. Его можно определить как совокупность упорядоченных пар, указывающих объекты, находящиеся в данном отношении.

Рассмотрим прямое произведение множеств AB

A B a,b a A,b B .

Назовем бинарным отношением R из A в B множество пар (a,b), для которых высказывание, связывающее a и b, и определяющее отношение R

истинно. В этом случае пишем aRb, (a,b) R или <a,b> R.

Областью определения бинарного отношения R называется множество

DR a | a A и b, b B, aRb Пр1R.

Область значений бинарного отношения R называется множество

GR bb B и a,a A,aRb Пр2 R. .

Очевидно, что DR A и GRB.

Например, если A – множество жителей Украины, B – множество населенных пунктов Украины, отношение R можно задать высказыванием

“быть жителем”, которое определяет пары (a,b)R, a A, bB такие, что высказывание “ a живет в населенном пункте b ” является истинным.

Рассмотрим множества A={1,2,3}, B={3,4,5,6}и определим отношение

R следующим образом:

a A, b B, aRb a+b 7.

Соответствующее отношению множество RAB имеет состав:

R={(1,3),(1,4),(1,5),(2,3),(2,4),(3,3)}.

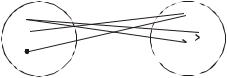
Графическое представление бинарного отношения на конечных множествах можно осуществить с помощью графа или таблицы. Для демонстрации последнего примера на рис.1.23. представлен граф отношения,

в котором участвующие в R пары указанны дугами. Таблица отношения имеет два входа, и элементы отношения выделяются единицами (табл. 1).

Таким образом, бинарное отношение R на конечных множествах

A={a1,…,am}, B={b1,…,bn} может быть задано матрицей C= сij размером mn, в которой:

1, если ai Rbj ,

cij

0, в противномслучае.

A B

13 24 35

6

Рис.1.23. Граф отношения, где дуга ai ,bj есть в графе, если

отношение, называемое пустым и которому не соответствует ни одна из пар

(a,b)AB. В противовес можно говорить и об отношении R=A B, которое содержит любую пару (a,b),aA, bB.

Если задано отношение RAB, то для любого A1 A определяется отношение R1, называемое сужением R на A1, которое получается из R

удалением всех пар, содержащих элементы, на принадлежащие M1, те

R1=R (A1 B)

Так как отношение R задается на множестве A B и R A B, т.е. R есть подмножество, то для него обычным образом определены теоретико-

множественные операции объединения, пересечения и т.д. Например,

отношение является объединением отношений и .

Если определено отношение R из A в B, то обратное отношение из B в A, обозначаемое R 1 , определяется тождеством

b R 1 a aRb, a A, b B,

или

R 1 ={(b,a) aRb}.

Например, Если R={(1,1), (1,2), (1,3), (3,4)}, то

R 1 ={(1,1), (2,1), (3,1), (4,3)}.

Свойства отношений

Рассмотрим множества A={3,4.5}, B={2,3,4}, C={5,6,7,8} и отношение

R1 a,b a A,b B,a b 7 ,

R2 { b,c b B,c C и b является делителем c}.

Композицию отношений R R1 R2 изобразим графом (рис.1.24). Из него видно, что R={(3,6),(3,8),(4,6),(4,8)},где в каждой паре (a,c) для элемента a найдется элемент b, такой, что он является делителем c.

Важным типом бинарных отношений являются те, в которых исходное множество A и конечное B совпадают, т.е. A=B. Тогда говорят об отношении из A в A или просто бинарным отношением R на A:

R ((a,b) a,b A,aRb}.

Используя такие отношения, можно задать, например, действительную

функцию f:

f x, x2 x 1 | x R ,

которая в обычной записи имеет вид y = x 2 +x+1.

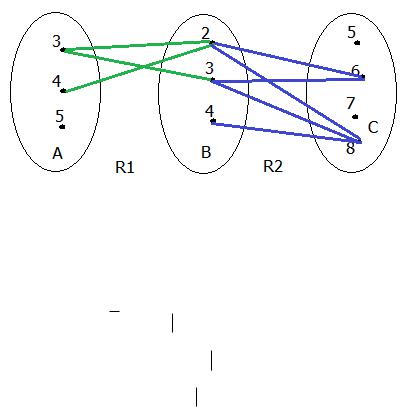
Рис.1.24. Композиция отношений

Для отношения R на A: R A A, a,b R , кроме обратного отношения можно ввести следующие понятия:

–дополнение отношения R a,b a,b R ;

–тождественное отношение I a,a a A ;

–универсальное отношение U a,b a A,b A .

Если R – отношение на множестве А, то степенью отношения R на А называется его n-композиция с самим собой

Rn R R R ,

Отметим, что R0 I , R1 R , … , Rn Rn 1 R .

Задание

1.Решите задачу на прямое произведение множеств в соответствии с условием.

2. Пусть А={1,2,3,4,5,6,7,8,9,10,11}. Определить отношение R, его область определения, область значений и обратное отношение, если отношения xRy задано. Построить матрицы отношений R и R-1. (Согласно варианту)

1.(x, y) R, если x y.

2.(x, y) R, если x y.

3.(x, y) R, если x y 2 .

4.(x, y) R, если y x 2 .

5.(x, y) R, если x делится y.

6.(x, y) R, если y делится на x

7.(x, y) R, если x y(mod3).

8.(x, y) R, если x y(mod2).

9.(x, y) R, если x y 3.

10.(x, y) R, если x y 7.

11.(x, y) R, если xr B, B {1,4,9,36,25}.

12. (x, y) R, если х и y имеют общий, не равный 1, делитель.

13.(x, y) R, если x y.

14.(x, y) R, если x y.

15.(x, y) R, если x2 y 10.

16.(x, y) R, если x2 y 2 (mod 3).

17.(x, y) R, если x y2 (mod 2).

18. (x, y) R, если x y2 (mod 3).

19.(x, y) R, если x y2 (mod 2).

20.(x, y) R, если x y2 (mod 3).

3. Найти отношение R R1 R2 и построить граф (по варианту), если: a) A={0,1,2,3}, B={2,4,5,8}, C={6,7,8,9}

отношение

R1 a,b a A,b B, a b 6 , R2 { b,c b B,c C c-b=2}.

b) A={1,2,3,4}, B={3,4,5}, C={5,7,8,10}

отношение

R1 a,b a A,b B, a b 8 ,

R2 { b,c b B,c C и c делится на b }.

c) A={2,4,5,6}, B={4,5,7}, C={2,3,5}

отношение

R1 a,b a A,b B, a b 3 ,

R2 { b,c b B,c C b c 10 }.