
дифуравнения / дифуравнения-1 / тема6
.docТема: Лінійні диференціальні рівняння вищих порядків. Лінійні однорідні рівняння з постійними коефіцієнтами
Теоретичні відомості
Означення. Рівняння
![]() ,
(2.9)
,
(2.9)
де
![]() неперервні
функції, визначені в інтервалі
неперервні
функції, визначені в інтервалі
![]() ,
називається лінійним
диференціальним рівнянням
,
називається лінійним
диференціальним рівнянням
![]() го
порядку.
го
порядку.
Якщо функція
![]() ,
то рівняння (2.9) називається лінійним
неоднорідним диференціальним рівнянням
,
то рівняння (2.9) називається лінійним
неоднорідним диференціальним рівнянням
![]() го
порядку. В разі, якщо
го
порядку. В разі, якщо
![]() ,
то рівняння (2.9) називається лінійним
однорідним диференціальним рівнянням
,
то рівняння (2.9) називається лінійним
однорідним диференціальним рівнянням
![]() го
порядку.
го
порядку.
Означення. Будь
– які рішення
![]() лінійного однорідного рівняння
лінійного однорідного рівняння
![]() , (2.10)
, (2.10)
для яких
![]() ,
називаються лінійно
незалежними.
,
називаються лінійно
незалежними.
Для знаходження загального
рішення однорідного рівняння (2.10) треба
знати
![]() лінійно
незалежних частинних рішень
лінійно
незалежних частинних рішень
![]() .
.
Теорема. Для того, щоб система рішень
![]() (2.11)
(2.11)
була лінійно незалежною, необхідно і достатньо, щоб визначник
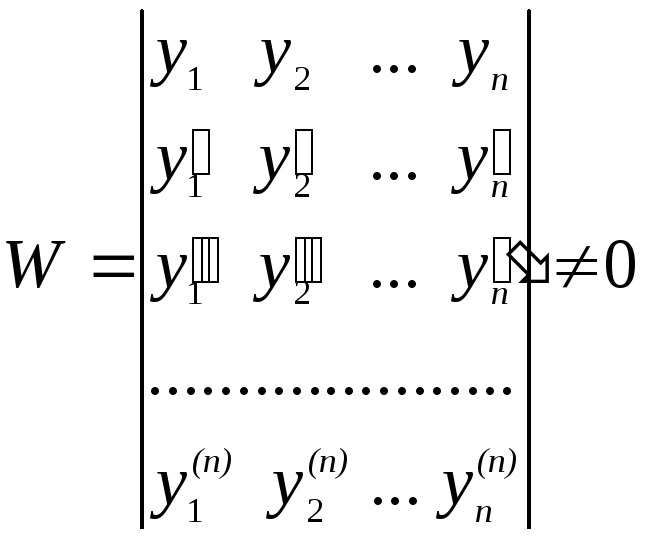 .
(2.12)
.
(2.12)
Означення. Визначник (2.12) називається визначником Вронського, а система рішень (2.11) – фундаментальною системою рішень рівняння (2.10).
Якщо відома фундаментальна система рішень (2.11) однорідного рівняння (2.10), то його загальне рішення має вигляд
![]() , (2.13)
, (2.13)
де
![]() довільні
константи.
довільні
константи.
Розглянемо лінійне однорідне
рівняння
![]() го
порядку з постійними коефіцієнтами
го
порядку з постійними коефіцієнтами
![]() , (2.14)
, (2.14)
де
![]() дійсні
константи.
дійсні
константи.
Побудуємо фундаментальну систему рішень. Частинне рішення рівняння (2.14) будемо шукати у вигляді
![]() , (2.15)
, (2.15)
де
![]() дійсне
або комплексне число, яке підлягає
визначенню. Знайдемо похідні функції
дійсне
або комплексне число, яке підлягає
визначенню. Знайдемо похідні функції
![]() :
:
![]() (2.16)
(2.16)
Підставляючи (2.15) і (2.16) в (2.14), отримаємо
![]() ,
,
або
![]() . (2.17)
. (2.17)
Рівняння (2.17) називається характеристичним рівнянням диференціального рівняння (2.14).
Структура загального рішення рівняння (2.14) залежить від вигляду коренів характеристичного рівняння (2.17):
1.
![]() дійсні
і різні корені. Тоді загальне рішення
має вигляд
дійсні
і різні корені. Тоді загальне рішення
має вигляд
![]() (2.18)
(2.18)
2.
![]() комплексно
спряжені корені. В загальному рішенні
цим кореням відповідає вираз вигляду
комплексно
спряжені корені. В загальному рішенні
цим кореням відповідає вираз вигляду
![]() . (2.19)
. (2.19)
3.
![]() дійсний
дійсний
![]() кратний
корінь. В загальному рішенні цьому
кореню відповідає вираз вигляду
кратний
корінь. В загальному рішенні цьому
кореню відповідає вираз вигляду
![]() . (2.20)
. (2.20)
4.
![]() комплексно спряжені корені кратності
комплексно спряжені корені кратності
![]() .
В загальному рішенні цим кореням
відповідає вираз вигляду
.
В загальному рішенні цим кореням
відповідає вираз вигляду
![]() . (2.21)
. (2.21)
Детальніше зупинимося на лінійному однорідному рівнянні другого порядку з постійними коефіцієнтами
![]() , (2.22)
, (2.22)
де
![]() дійсні
числа.
дійсні
числа.
Загальне рішення рівняння (2.22) має вигляд
![]() , (2.23)
, (2.23)
де
![]() фундаментальна
система рішень.
фундаментальна
система рішень.
Рівнянню (2.22) відповідає характеристичне рівняння
![]() . (2.24)
. (2.24)
Отже, знаходження частинних рішень рівняння (2.22) зводиться до розв’язання квадратного рівняння (2.24):
-
Нехай
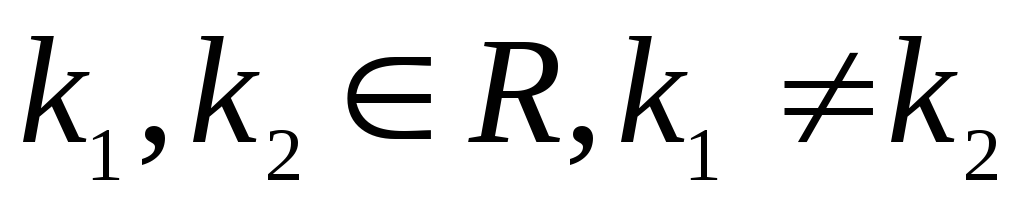 .
Тоді
.
Тоді
![]() . (2.25)
. (2.25)
-
Нехай
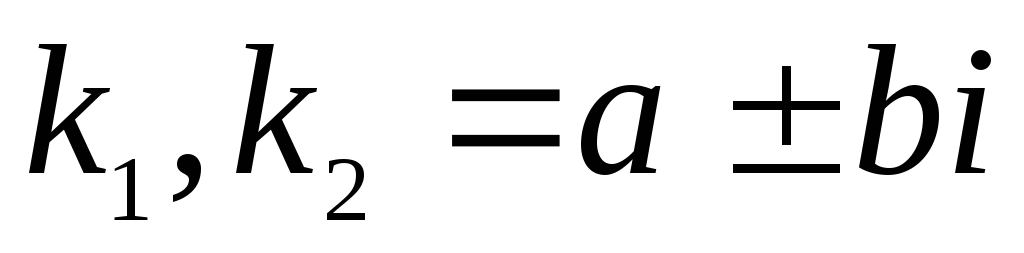 .
Тоді
.
Тоді
![]() . (2.26)
. (2.26)
-
Нехай
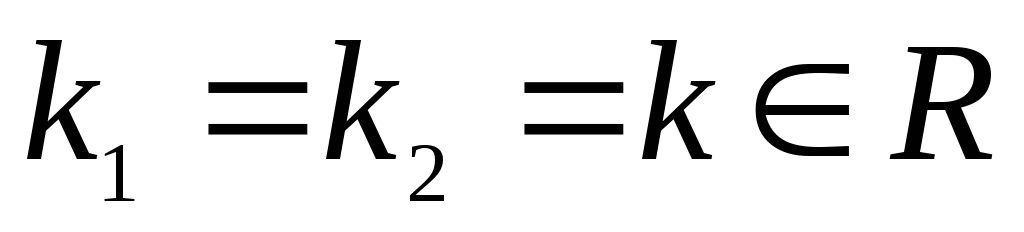 .
Тоді
.
Тоді
![]() . (2.27)
. (2.27)
Практичні завдання
Завдання 1. Скласти характеристичне рівняння лінійного однорідного рівняння з постійними коефіцієнтами:
1.1
![]() .
.
1.2.
![]() .
.
1.3.
![]() .
.
1.4.
![]() .
.
1.5.
![]() .
.
1.6.
![]() .
.
1.7.
![]() .
.
1.8.
![]()
1.8.
![]() .
.
1.9.
![]() .
.
1.10.
![]() .
.
1.11.
![]() .
.
Завдання 2. Знайти загальне рішення лінійного однорідного рівняння з постійними коефіцієнтами, якщо відомі корені характеристичного рівняння:
2.1.
![]() .
.
2.2.
![]() .
.
2.3.
![]() .
.
2.4.
![]() .
.
2.5.
![]() .
.
2.6.
![]() .
.
2.7.
![]() .
.
2.8.
![]() .
.
2.9.
![]() .
.
Завдання 3. Скласти лінійне однорідне рівняння ІІ порядку з постійними коефіцієнтами, якщо відоме його загальне рішення:
3.1.
![]() .
.
3.2.
![]() .
.
3.3.
![]() .
.
Завдання 4. Проінтегрувати рівняння із завдання 1.
Завдання 5. Розв’язати задачу Коші:
5.1.
![]() ,
якщо
,
якщо
![]() .
.
5.2.
![]() ,
якщо
,
якщо
![]() .
.
5.3.
![]() ,
якщо
,
якщо
![]() .
.
5.4.
![]() ,
якщо
,
якщо
![]() .
.
5.5.
![]() ,
якщо
,
якщо
![]() .
.
5.6.
![]() ,
якщо
,
якщо
![]() .
.
5.7.
![]() ,
якщо
,
якщо
![]() .
.
