3.Интегрирование по частям

Применение формулы (*)

к нахождению первообразной называется интегрирование по частям. К интегрированию по частям относятся случаи, когда подынтегральное выражение содержит:

а) произведение вида ;

б) логарифмические функции;

в) обратные тригонометрические функции;

г) некоторые другие функции.

Чтобы применить формулу интегрирования по частям, надо все подынтегральное выражение разбить на два множителя, один из которых обозначить , а другой. При этом: 1)должен быть отнесен к; 2)должен быть таким, чтобы интегрированием можно было легко найти, так как(константуне добавлять!). Обычно руководствуются правилом: занадо брать такую функцию из подынтегрального выражения, которая при дифференцировании упрощается; а остальная часть имеет известный интеграл.

В выборе ив значительной мере поможет следующая таблица.

№	Вид интеграла	Сомножитель		Сомножитель
1.	многочлен
2.	многочлен	=
3.			Возможен любой выбор сомножителей
4.
5.

Применяя формулу интегрирования по частям, мы не сразу находим первообразную, а заданный интеграл приводим к другому (смотри форму-лу (*)), и если этот интеграл проще заданного или табличный, то формула применена правильно.

1) Найти

Обозначим ;.

Найдем ;.

Подставляя в формулу (*), получим

=

.

К последнему интегралу вновь применяем формулу интегрирования по частям.

Положим ;.

Тогда ;.

По формуле (*), получим:

.

2) Найти .

Пусть ;.

Тогда ;.

Подставляя в формулу (*), получим:

.(**)

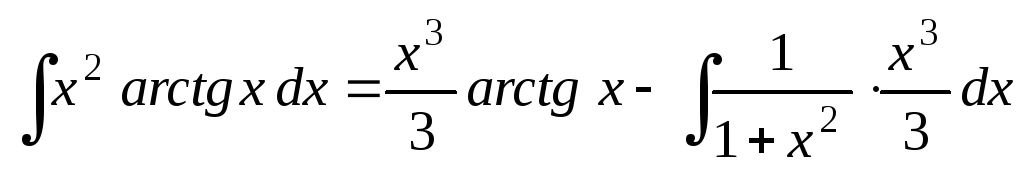Последний интеграл вычислим отдельно

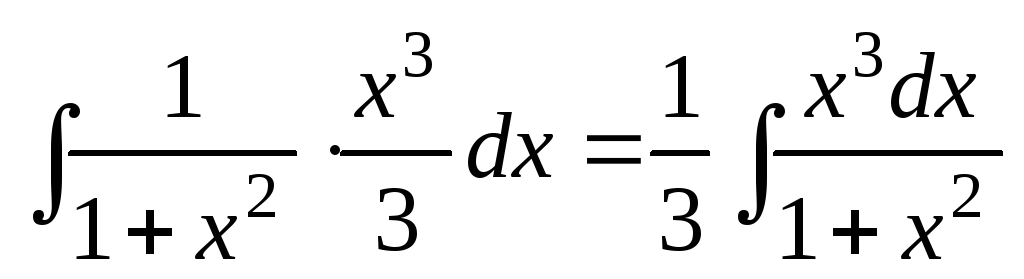. Этот интеграл от неправильной рациональной дроби.

Выделим целую часть:

.

Формулa:

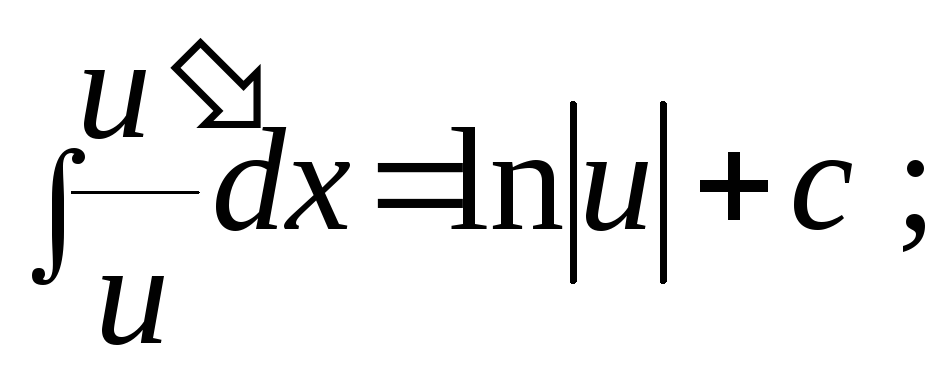
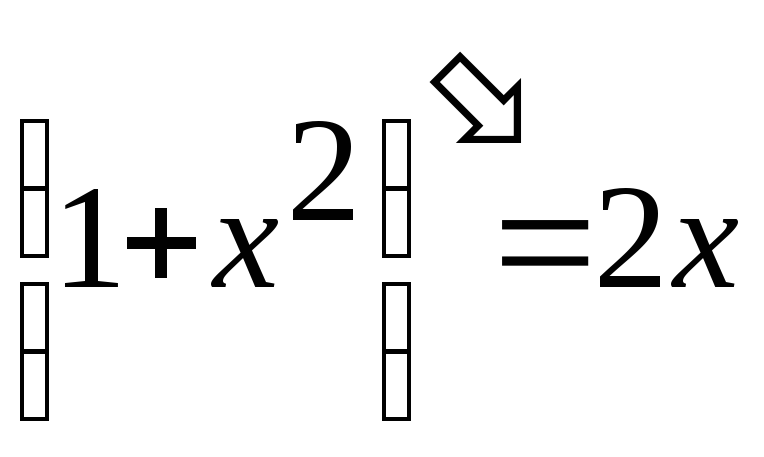
Подставляя полученный результат в равенство (**), имеем

3) Найти .

Пусть ;.

Тогда ;.

По формуле (*), имеем:

(***)

К полученному интегралу снова применим интегрирование по частям.

Полагая ,, получим:

,

.

Подставляя этот результат в (***), получим:

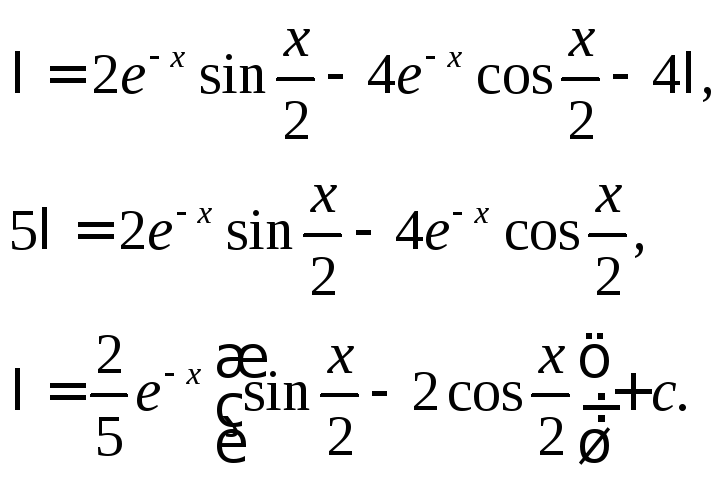
Это решение показывает, что повторное интегрирование по частям может привести к исходному интегралу.

Методом интегрирования по частям находятся интегралы №1(в)-10(в)

4. Интегрирование некоторых тригонометрических функций

а) Интегралы вида .

Рассмотрим случай, когда ичетные. Тогда применяются формулы понижения степени,.

1) Найти =

Первые два интеграла представляют табличные формулы. Последний интеграл найдем отдельно, применяя формулу понижения степени.

.

Подставляя в предыдущее равенство, получим.

Рассмотрим случай, когда либо , либонечетные (или и, инечетные)

От нечетной степени синуса или косинуса отделяют один множитель и находят интеграл путем замены кофункции новой переменной.

2) Найдем .

Введем новую переменную: Пусть тогдаПолучим

Интегралы вида (или), гдецелое положительное число вычисляются с помощью формулы(или соответственно).

Интегралы такого вида можно найти также путем замены , или соответственно,новой переменной.

3) Найти.

Пусть , тогда;,

.

Выделим целую часть в подынтегральной дроби:

;

.

=.

Формула: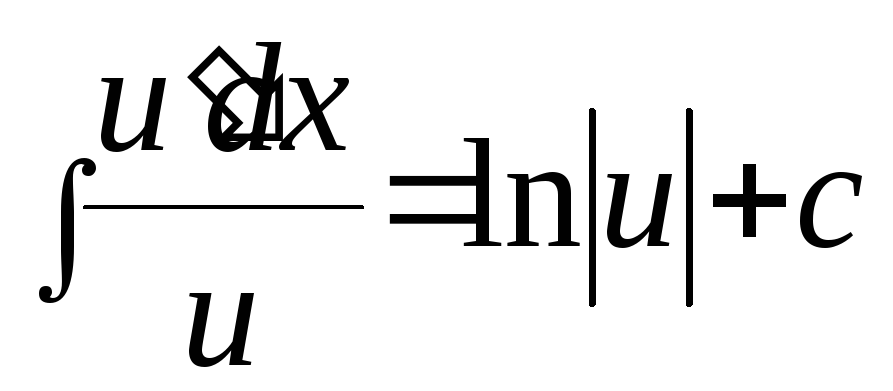

Интегралы вида , где- рациональная функция, зависящая оти, приводятся с помощью подстановки, откуда;, к интегралам от рациональных функций новой переменной.

4) Найти .

Полагая , имеем:

.

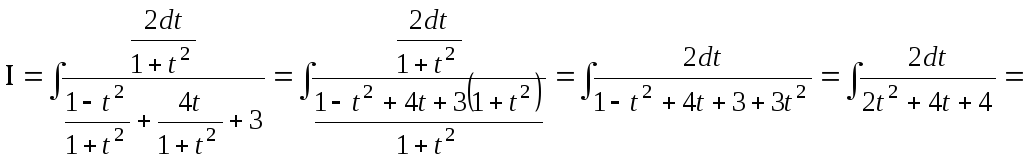
Формула: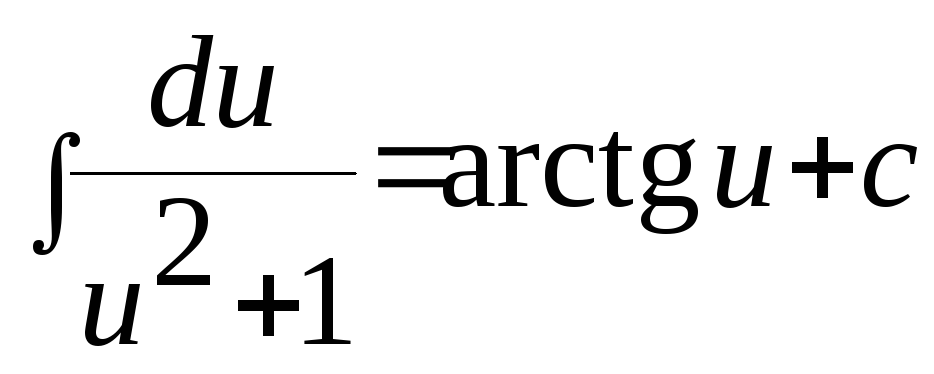

Возвращаясь к старой переменной, получим:

.

Интегрирование тригонометрических функций имеет место в №11(в)-20(в)