4. Некоторые геометрические положения определенных интегралов

а) Вычисление площадей плоских фигур

Площадь криволинейной трапеции, ограниченной кривой двумя вертикальными прямыми в точкахии отрезком оси абсцисс, определяется формулой

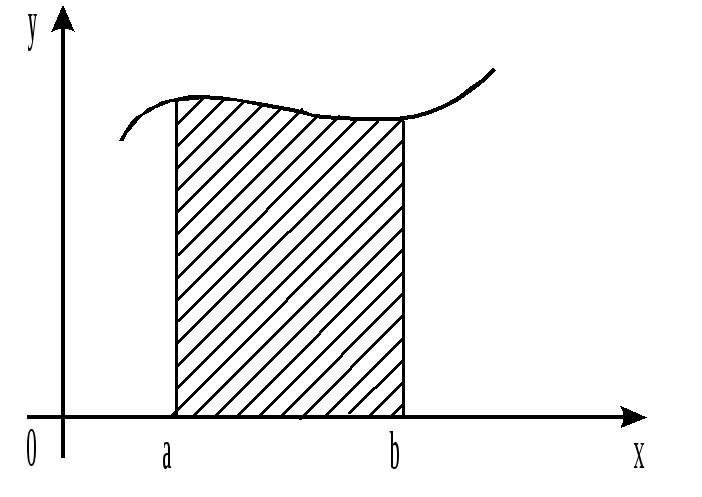
Если плоская фигура ограничена кривыми ии двумя прямыми, то ее площадь определяется формулой

.

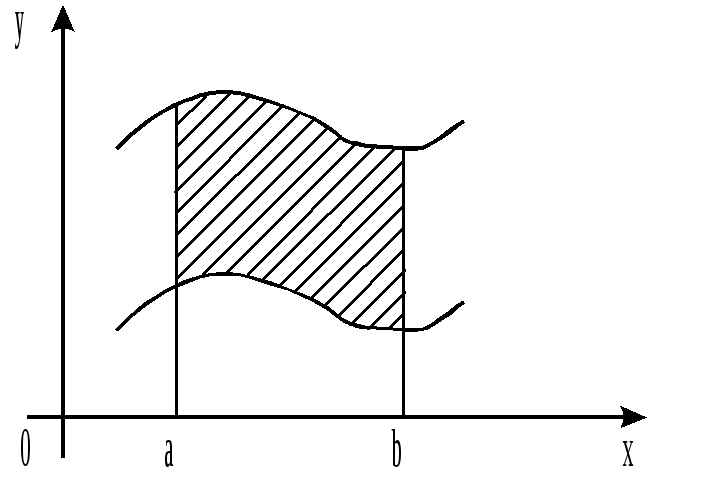
Вычислить площадь фигуры, ограниченной линиями .

Решая совместно данные уравнения 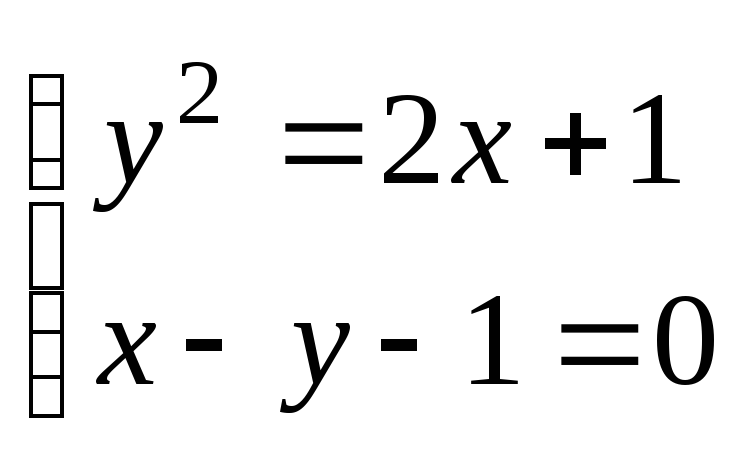, найдем точки пересечения этих линий

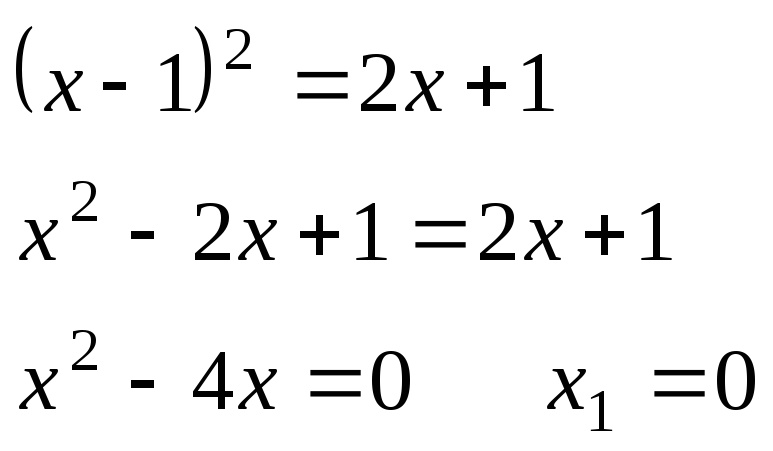
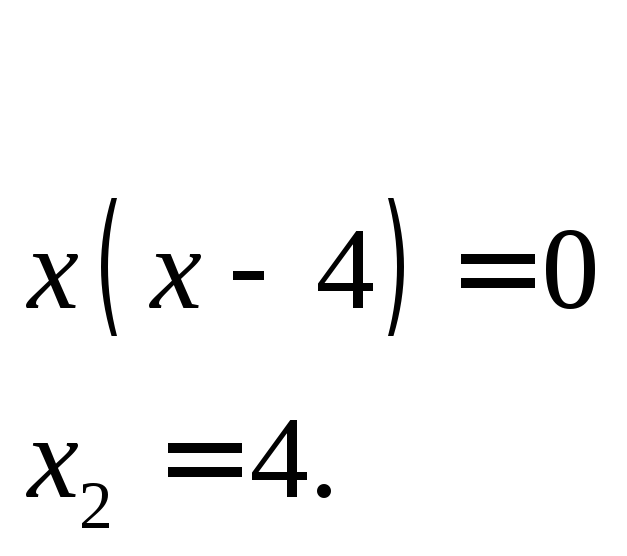
И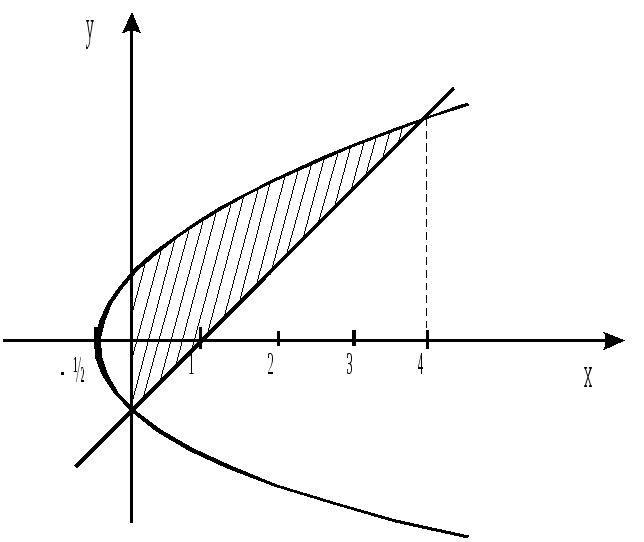зобразим в плоскости ХОУ фигуру, ограниченную данными линиями, причемсогласно условия.

yx–1

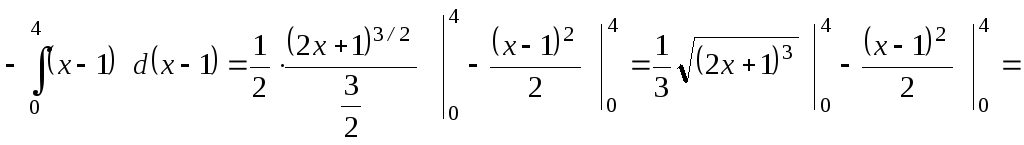
(ед.²).

Если кривая задана в параметрической форме:

то .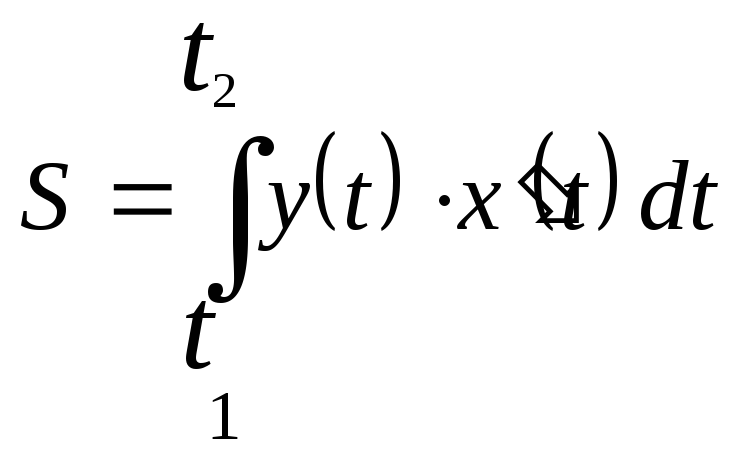

Вычислим площадь эллипса, заданного в параметрической форме:

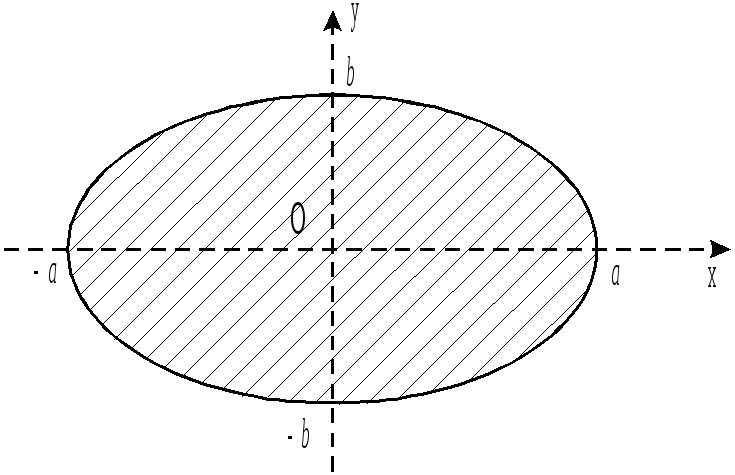
Решение:

Площадь эллипса где- площадьчасти эллипса

при ,;

при ,.

.

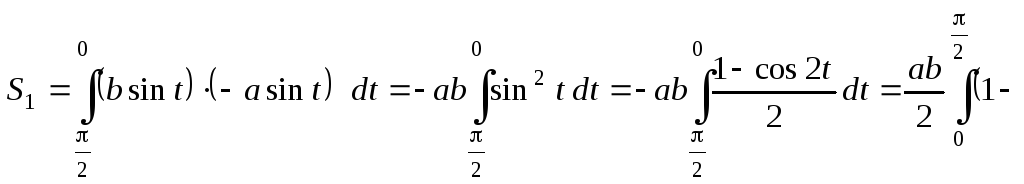
Площадь эллипса .

Если кривая задана в полярной системе координат , то площадь криволинейного сектора определяем по формуле:

где.

Вычислить площадь, ограниченную кардиоидой .

Кардиоида симметрична по-

лярной оси, поэтому искомая

площадь равна удвоенной пло-

щади сектора .

Поэтому согласно формуле имеем:

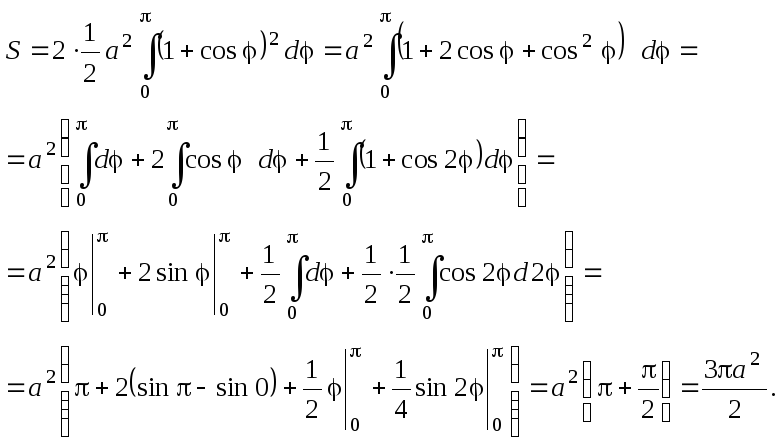
б) Длина дуги кривой

В прямоугольных координатах длины дуги гладкой кривой, содержащейся между двумя точками с абсциссамии, равна.

Если кривая задана уравнениями в параметрической форме ,, то длина дуги

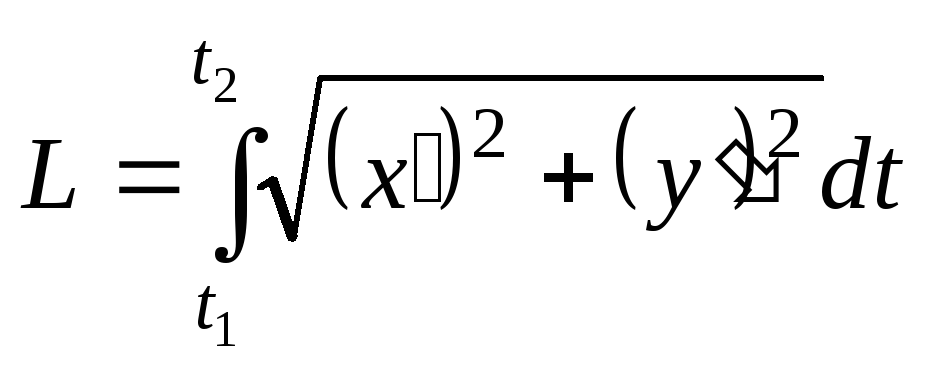, гдеи- значения параметра, соответствующие концам дуги.

Если кривая задана уравнением в полярных координатахи, то длина дугиравна

, гдеи- значения полярного угла в крайних точках.

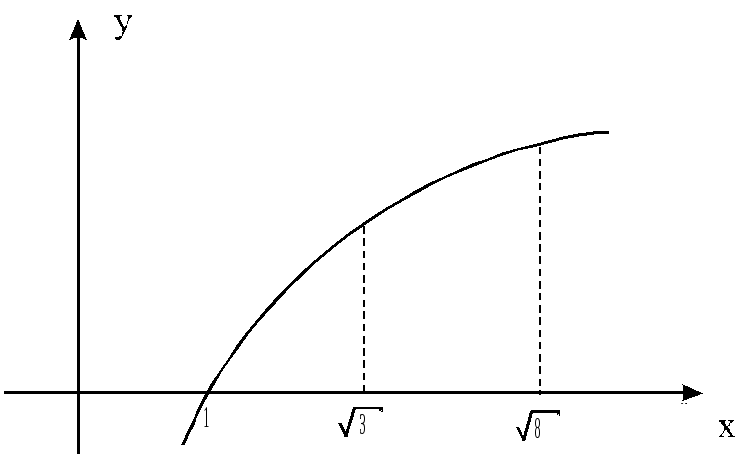
Вычислить длину кривой отдо.

Кривая задана в прямоугольных координатах. Длина дуги определяется по формуле

. Домножим числитель и знаменатель подынтегральной дроби на. Получим:

. Введем замену:

,,;

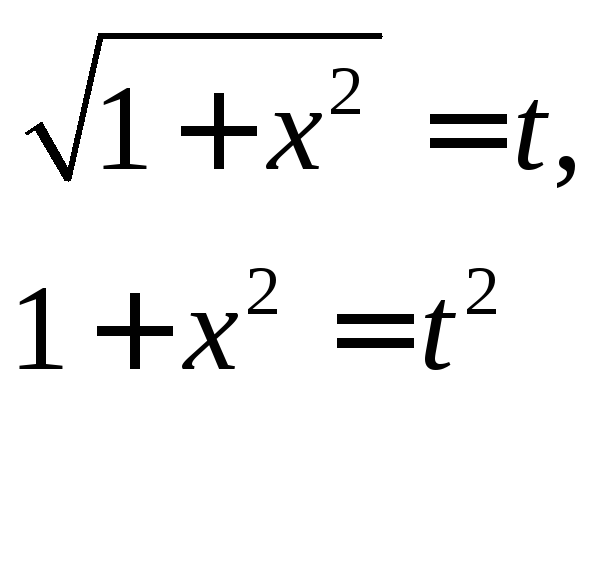при ,;

при ,.

Получим

.

Длина дуги кривой .

Задачи №№ 61-80 на приложения определенного интеграла к задачам физического или геометрического содержания. Соответствующие формулы можно найти в справочной литературе, например: М.Я. Выгодский. Справочник по высшей математике. Москва – 1975 г. парагр. 334-341.

5. Несобственные интегралы

а) Если функция непрерывна при, то полагают

и в зависимости от существования или не существования конечного предела в правой части равенствасоответствующий интеграл называется сходящимся или расходящимся.

Аналогично

;

.

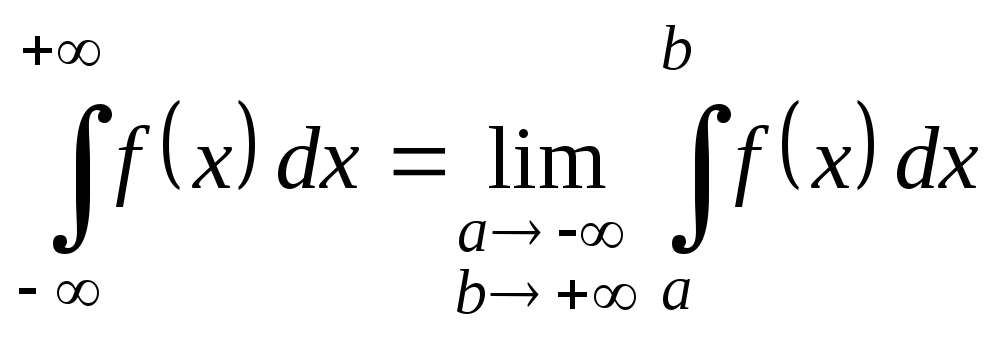Если и интегралсходится, тотоже сходится.

Если иприто:

а) при интегралсходится;

б) при интегралрасходится.

Пример 1. Вычислить несобственный интеграл или установить его расходимость.

.

.

Вычислим отдельно

.

Тогда .

Следовательно, данный несобственный интеграл сходится.

Пример 2.Вычислить несобственный интеграл или установить его расходимость.

.

.

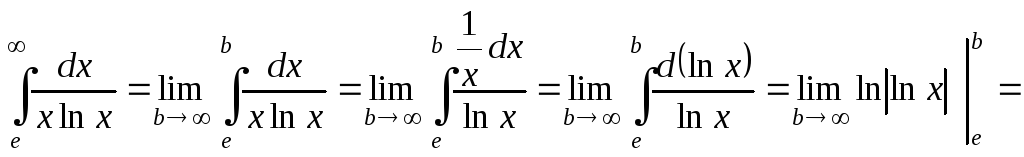
Следовательно, данный несобственный интеграл расходится.

б) Интегралы от неограниченных функций

Если функция не ограниченна в любой окрестности точки с отрезкаи непрерывна прии, то по определению полагают:

.

Если пределы в правой части равенства существуют и конечны, то несобственный интеграл называется сходящимся, в противном случае – расходящимся.

Если приисходится, то интегралтакже сходится (признак сравнения).

Если ипри, то:

а) при интегралсходится,

б) при интегралрасходится.

Пример 1. Вычислить несобственный интеграл или установить его расходимость

.

Подынтегральная функция принеограниченна (т.е. терпит разрыв).

Следовательно, данный несобственный интеграл расходится.

Пример 2. Вычислить несобственный интеграл или установить его расходимость

.

При подынтегральная функцияимеет разрыв.

.

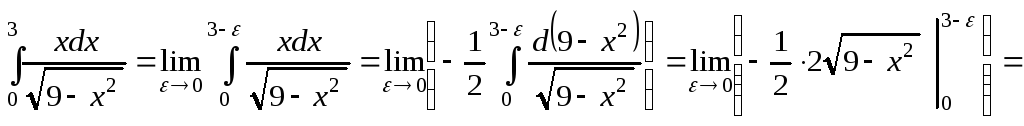
Следовательно, данный несобственный интеграл сходится.

Пример 3. Исследовать сходимость интеграла ;

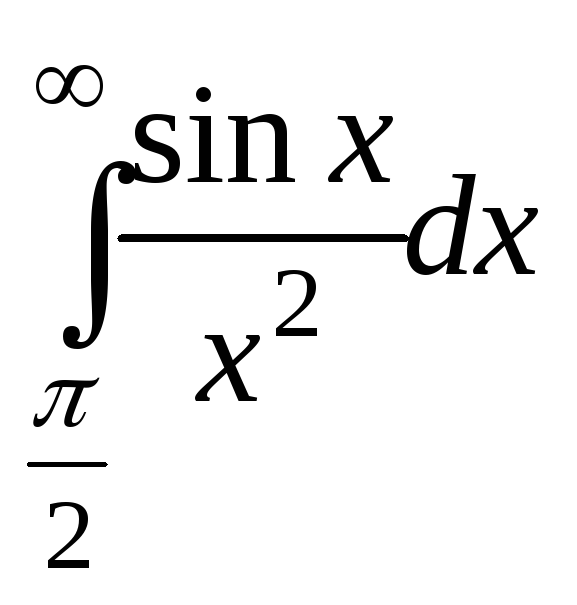при ;, т.к., то

.

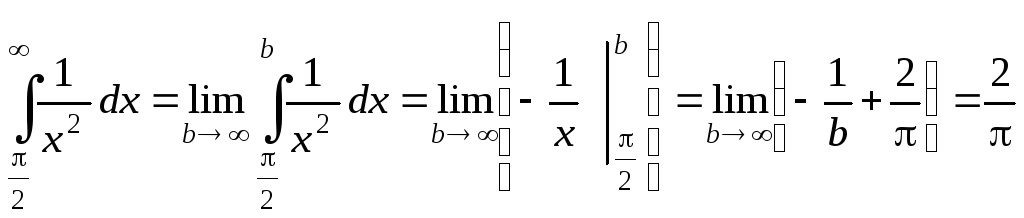Интеграл сходится, т.к. 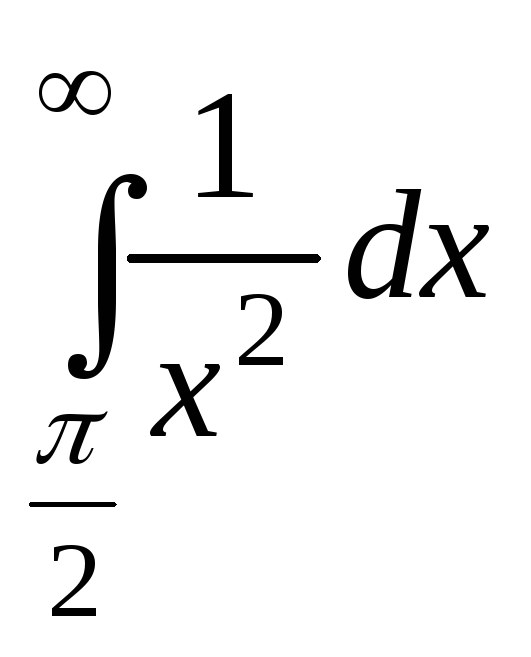сходится, ипри, то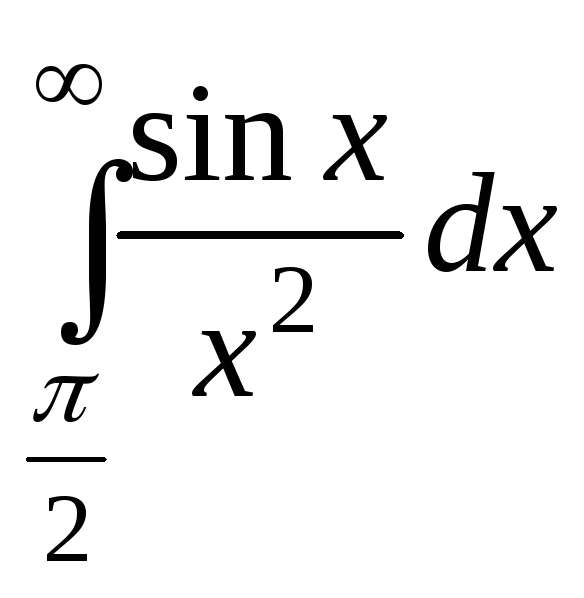тоже сходится.