
Шпоры по вышке 1
.doc
1.Множество-совокупность
объектов произвольной природы. Эти
объекты называются элементами мн-ва.
Мн-во обозначаются заглавными буквами:
A,B,C,
а их эл-ты строчными: a,b,c.
При описании мн-в их эл-ты заключают в
фигурные скобки А={а1,а2…}.
Мн-во, не содержащее ни одного эл-та,
называется пустым (Ø). Основные
числовые мн-ва:
1)N={1,2,…}-мн-во
натур.чисел; 2){2n:nєN}-мн-во
четн.чисел; 3)Z={0,±1,±2,…}-мн-во
целых чисел; 4)Q={m/n:
mєZ,nєN}-мн-во
рацион.чисел,конечных и период.десят.дробей;
5)R-мн-во
действ.чисел, мн-во период. и
непереод.десят.дробей(ирацион.);
6)[a,b]={xєR:a≤x≤b}-замкн.числ.промеж.(отрезок);
7)(а,b)={xєR:a<x<b}-открыт.числ.промеж.(интервал);
8)[a,b)={xєR:a≤x<b};
9)(a,b]-{xєR:a<x≤b}-
полуинтервалы. Операции
над мн-ми:
1) произведение(пересечение) X![]() Y={z:zєX
и zєY};
2)объединение(сумма) X
Y={z:zєX
и zєY};
2)объединение(сумма) X![]() Y={z:zєX
или zєY};
3) разность X\Y={z:zєX
и z
Y={z:zєX
или zєY};
3) разность X\Y={z:zєX
и z![]() Y}
2.
Способы
задания ф-ции:
1)
табличный, 2) графический, 3) аналитический
(явный-с помощью 1 или нескольк.выраж.;
неявный- с помощью ур-ия F(x,y)=0;
параметрический-с помощью системы).
Классификация:
четная f(-x)=f(x)
, нечетная f(-x)=-f(x);
монотонная-убыв., возраст.,неубыв..,невозраст.ф-ция.
Периодич.ф-ция-ф-ция, имеющая период
(Т), при котором f(х-Т)=f(x)=f(х+Т).
Элементрные
ф-ции
1)степенн. y=xα;
2)показат. y=ax
a>0
;
3)логарифм. Y=logax
a>0
a≠1;
4)тригоном. y=sinx,
y=cosx,
y=tgx,
y=ctgx;
5) обратн.тригоном. y=arcsinx,
y=arccosx,
y=arctgx,
y=arcctgx;
6) постоянн. y=const.
3.
Ф-ция
как отображение.
Если каждому эл-ту х мн-ва Х поставлен
в соответствие единственный элемент y
мн-ва Y,
то говорят, что задано
отображение мн-ва
X
в мн-во Y,
которое обозначается f:X→Y
или y=f(x),
xєX.
Здесь Х-мн-во определения(обозначается
Df
),
Rf={y|y=f(x),xєX}-мн-во
значений. Графиком ф-ции является мн-во
всех точек (x,y)
плоскости Oxy,
для каждой из которых значение аргумента
x
является абсциссой, а значение y=y(x)
ф-ции-ординатой. Сложная
ф-ция Сложная
функция-это функция от функции. Если y
является ф-цией от u, то есть у = f (u), а u,
в свою очередь, функцией от х, то есть u
= j(х), то у является сложной ф-цией от х,
то есть y = f [u(x)].
Т.е. у является сложной ф-цией независимого
аргумента х, а u — промежуточным
аргументом. Обратная
ф-ция
Если
есть y=f(x),
то x=f-1(y)
является обратной, при этом каждому
числу yєRf
ставится
в соответствие единственное число xєDf
.
Св-ва
обратной ф-ции 1)
Графики взаимно обратных функций
симметричны относительно прямой y=x. 2)
Если прямая ф-ция возраст.(убыв.), то и
обратная возраст.(убыв.). 3) Область
определения прямой ф-ции совпадает с
областью значений обратной ф-ции и
наоборот. 4.
Открытые
мн-ва на прямой Множество
называется открытым, если каждая его
точка является для него внутренней:
(a,b)-открытое
мн-во. Окрестность.
Окрестностью B(a)
точки aєR
называется любой интервал, содержащий
эту точку. Предел.
На языке окрестностей.
Число b
называется пределов ф—ции y=f(x)
при x→a,
если для любой окрестности B(b)
точки b
найдется такая проколотая окрестность
B^(a)
точки a,
что как только xєB^(a),
то f(x)єB(b),
что обозначается b=limf(x)
при x→a.
Св-ва
пределов.
1) Предел суммы(разности) двух ф-ций равен
сумме(разности) пределов этих ф-ций; 2)
Предел постоянной величины равен самой
постоянной величине; 3) Предел произведения
двух ф-ций равен произведению пределов
этих ф-ций (при условии, что последние
существуют);4) Предел частного двух ф-ций
равен отношению пределов этих ф-ций при
условии, что предел знаменателя не равен
нулю. 5.
Предел
ф-ции одной переменной на языке «ɛ-δ»:
число b
называется пределом ф-ции y=f(x)
при x→a,
если для любого как угодно малого ɛ>0
найдется такое число δ>0, что для всех
x,
удовлетворяющих условию |x-a|<δ,
x≠a,
будет выполняться неравенство |f(x)-b|<ɛ.
6.
Предел
последовательности. Пределом
последовательности элементов пространства
называют элемент того же пространства,
который обладает свойством «притягивать»
элементы данной последовательности.
Последовательностью
{xn}
называется упорядоченное счетное
множество чисел {x1,x2,x3..}.
Св-ва.
1)Если последовательность сходится, то
ее предел единственный; 2)Если
последовательность сходится, то она
ограничена; 3)Если последовательность
сходится к числу >0, то вся последовательность
лежит вне окрестности нуля, начиная с
некоторого номера.7.
Бесконечно
малые и большие ф-ции.
Ф-ция
y=α(x)
бесконечно
малая
при x→a,
если lim
α(x)=0(т.е.
для любого сколь угодно малого ε>0
найдётся такая проколотая окрестность
точки a,
что для всех x
из этой окрестности справедливо
неравенство |α(x)|<
ε.)
Свойства
бмф:1)Алгебраическая
сумма конечного числа бесконечно малых
функций есть бмф;
2)Произведение бесконечно малой функции
на ограниченную функцию есть бмф;
3)Если α(x)~β
(x),
то β
(x)~α(x);
4)Если α(x)~β
(x)
и β
(x)~γ(x),
то α(x)~γ(x);
5)Если α(x)~β
(x),
то и α(x)-β
(x)=о
(α(x))=о(β
(x));
6)Если α(x)~
α'(x)
и β
(x)~
β'(x),
то lim
β
(x)/
α(x)=
lim
β'(x)/
α'(x)
(x→a);
Функция y=β(x)
бесконечно
большая
при x→a,
если lim
β
(x)=бесконеч.
или lim
|β
(x)|=+бесконеч.
Свойства
ббф:1.
Если в некоторой прокол.окрестности
точки а
функция
α(x)≠0
и является бмф
при x→a,
то β
(x)=1/
α(x)
есть ббф
при x→a
и наоборот; 2)Произведение ббф
на функцию |f(x)|
>M≠0
есть ббф;
3)Сумма бесконечно большой и ограниченной
ф-ции есть ббф;
4)Сумма двух ббф
одинакого знака есть ббф.
8.
Сравнение
бесконечно малых ф-ций
производится путем нахождения предела
их отношений. Пусть α(x)
и β
(x)
– бмф
при
x→a,
причем lim
β
(x)/
α(x)=А.Тогда
если 1)А=1, то α(x)
и β
(x)
называются эквивалентными
бмф при
x→a,
что записывается в виде α(x)~β
(x);
2)А ≠0 и А=бесконеч., то α(x)
и β
(x)
– бмф
одного порядка малости
при x→a;
3)А=0, то β
(x)
есть бмф
более высокого порядка малости,
чем α(x),
при x→a,
что записывается в виде β
(x)=
о(α(x));
4)А=бесконеч., то α(x)
есть бмф более высокого порядка малости,
чем β
(x),
при x→a,
что записывается в виде α(x)=о(β
(x)).При
решении пределов
использование эквивалентных бесконечно
малых ф-ций в произведениях и частном.
При нахождении пределов бесконечно
малые множители, стоящие в числителе и
знаменателе заменяются им эквивалентными:
lim
f
(x)*p(x)/
g(x)=
lim
α (x)*γ(x)/
β(x),
если f
(x)
~α(x),
g(x)
~ β
(x),
p(x)
~ γ(x).9.
Основные теоремы о пределах. 1)теорема
о конечном пределе limf(x)=b↔f(x)=b+α(x)
при x→a;
2)теорема о связи с одностор.пределами:
limf(x)=b↔f(a-0)=f(a+0)=b
при x→a;
3)арифм.операции над пределами: умножение
на число: {xn}∙c={x1∙c,x2∙c..};
сложение и вычитание: {xn}±{yn}={x1±y1,
x2±y2..};
умножение и деление(если знаменатель
не равен 0) {xn}∙{yn}={x1∙y1,
x2∙y2..}
и {xn}/{yn}={x1/y1,
x2/y2..}
10.
Первый
зам. предел
limx->0(sinX)/X=1
используется для неопределенностей
вида [0/0] содержащих тригонометр. функции
. Пример:
Limx->0(tgX)/X=
Limx->0(sinX)/(X*CosX)=Limx->0sinX/X*Limx->01/cosX=[1/1]=1
Табл.
Эквивалентности: sinX=X;
tgX=X;
arcsinX=X;
arctgX=X;
1-cosX=X2/2;
cos2X=1-2sin2X
11.
Второй
зам. предел
limx->беск.(1+1/х)х=
Limx->0(1+х)1/х=е
используется для неопределенностей
вида [1беск.]
. Пример:
Limx->0(ln(x+4)-ln4)/x=
Limx->0(ln(x+4)/4)/x=1/4*Limx->0(ln(1+x/4))/(x/4)=1/4
Табл.
Эквивалентности: ex-1=x;
ln(1+x)=x;
ax-1=x*lna;
loga(1+x)=x*logae;
ln(x+√(x+1))=x;
(1+x)2-1=2x;
√(1+x)-1=x/2
12.
Определение
непрерывности ф-ции в точке. Ф-ция
y=f(x)
непрерывна в точке x0,если
f(x)
определена в точке x0
и
некоторой ее окрестности и limf(x)=f(x0)
при x→x0
13.Условие
непрерывности f(x)
непрерывна при x=x0
только в том случае, если 1)ф-ция определена
в точке x0;
2)если f(x0-0)f(x0+0)=f(x0)
Классификация
точек разрыва
Точки
разрыва 1 рода:1)т-ка устранимого разрыва
limf(x0-0)=limf(x0+0)=KєR,
f(x0)≠K
2)т-ка конечного скачка limf(x0-0)≠limf(x0+0)
Точки разрыва 2 рода 1)т-ка бесконечного
скачка: если оба предела существуют и
хотя бы 1 равен бесконечн.; 2)т-ка не
существования: если хотя бы один предел
не существует.
Все элементарные функции являются
непрерывными
в любой точке свой области определения.
14.
Свойства
функций, непрерывных на замкнутом
промежутке, и применение при исследовании
уравнений и неравенств.Если
функция f непрерывна
в замкнутой и ограниченной области Ω,
то:1)
функция f ограничена
на Ω ,
то есть существует такая постоянная M ,
что |f(x)|≤M при
всех xєΩ ;2)
функция f принимает
в области Ω наибольшее
и наименьшее значения, то есть существуют
такие точки x1єΩ и x2єΩ ,
что при всех xєΩ выполняются
неравенства f(x)≥f(x1) и.
f(x)≥f(x2) (В
этом случае точка x1 называется точкой
минимума,
а точка x2 -- точкой
максимума функции f в
области Ω .) 15.Производная
и её связь с дифференциалом, геом и
механ смысл производной и
дифференциала.Производной функции y = f ( x )
в точке x0 называется
предел:
Y}
2.
Способы
задания ф-ции:
1)
табличный, 2) графический, 3) аналитический
(явный-с помощью 1 или нескольк.выраж.;
неявный- с помощью ур-ия F(x,y)=0;
параметрический-с помощью системы).
Классификация:
четная f(-x)=f(x)
, нечетная f(-x)=-f(x);
монотонная-убыв., возраст.,неубыв..,невозраст.ф-ция.
Периодич.ф-ция-ф-ция, имеющая период
(Т), при котором f(х-Т)=f(x)=f(х+Т).
Элементрные
ф-ции
1)степенн. y=xα;
2)показат. y=ax
a>0
;
3)логарифм. Y=logax
a>0
a≠1;
4)тригоном. y=sinx,
y=cosx,
y=tgx,
y=ctgx;
5) обратн.тригоном. y=arcsinx,
y=arccosx,
y=arctgx,
y=arcctgx;
6) постоянн. y=const.
3.
Ф-ция
как отображение.
Если каждому эл-ту х мн-ва Х поставлен
в соответствие единственный элемент y
мн-ва Y,
то говорят, что задано
отображение мн-ва
X
в мн-во Y,
которое обозначается f:X→Y
или y=f(x),
xєX.
Здесь Х-мн-во определения(обозначается
Df
),
Rf={y|y=f(x),xєX}-мн-во
значений. Графиком ф-ции является мн-во
всех точек (x,y)
плоскости Oxy,
для каждой из которых значение аргумента
x
является абсциссой, а значение y=y(x)
ф-ции-ординатой. Сложная
ф-ция Сложная
функция-это функция от функции. Если y
является ф-цией от u, то есть у = f (u), а u,
в свою очередь, функцией от х, то есть u
= j(х), то у является сложной ф-цией от х,
то есть y = f [u(x)].
Т.е. у является сложной ф-цией независимого
аргумента х, а u — промежуточным
аргументом. Обратная
ф-ция
Если
есть y=f(x),
то x=f-1(y)
является обратной, при этом каждому
числу yєRf
ставится
в соответствие единственное число xєDf
.
Св-ва
обратной ф-ции 1)
Графики взаимно обратных функций
симметричны относительно прямой y=x. 2)
Если прямая ф-ция возраст.(убыв.), то и
обратная возраст.(убыв.). 3) Область
определения прямой ф-ции совпадает с
областью значений обратной ф-ции и
наоборот. 4.
Открытые
мн-ва на прямой Множество
называется открытым, если каждая его
точка является для него внутренней:
(a,b)-открытое
мн-во. Окрестность.
Окрестностью B(a)
точки aєR
называется любой интервал, содержащий
эту точку. Предел.
На языке окрестностей.
Число b
называется пределов ф—ции y=f(x)
при x→a,
если для любой окрестности B(b)
точки b
найдется такая проколотая окрестность
B^(a)
точки a,
что как только xєB^(a),
то f(x)єB(b),
что обозначается b=limf(x)
при x→a.
Св-ва
пределов.
1) Предел суммы(разности) двух ф-ций равен
сумме(разности) пределов этих ф-ций; 2)
Предел постоянной величины равен самой
постоянной величине; 3) Предел произведения
двух ф-ций равен произведению пределов
этих ф-ций (при условии, что последние
существуют);4) Предел частного двух ф-ций
равен отношению пределов этих ф-ций при
условии, что предел знаменателя не равен
нулю. 5.
Предел
ф-ции одной переменной на языке «ɛ-δ»:
число b
называется пределом ф-ции y=f(x)
при x→a,
если для любого как угодно малого ɛ>0
найдется такое число δ>0, что для всех
x,
удовлетворяющих условию |x-a|<δ,
x≠a,
будет выполняться неравенство |f(x)-b|<ɛ.
6.
Предел
последовательности. Пределом
последовательности элементов пространства
называют элемент того же пространства,
который обладает свойством «притягивать»
элементы данной последовательности.
Последовательностью
{xn}
называется упорядоченное счетное
множество чисел {x1,x2,x3..}.
Св-ва.
1)Если последовательность сходится, то
ее предел единственный; 2)Если
последовательность сходится, то она
ограничена; 3)Если последовательность
сходится к числу >0, то вся последовательность
лежит вне окрестности нуля, начиная с
некоторого номера.7.
Бесконечно
малые и большие ф-ции.
Ф-ция
y=α(x)
бесконечно
малая
при x→a,
если lim
α(x)=0(т.е.
для любого сколь угодно малого ε>0
найдётся такая проколотая окрестность
точки a,
что для всех x
из этой окрестности справедливо
неравенство |α(x)|<
ε.)
Свойства
бмф:1)Алгебраическая
сумма конечного числа бесконечно малых
функций есть бмф;
2)Произведение бесконечно малой функции
на ограниченную функцию есть бмф;
3)Если α(x)~β
(x),
то β
(x)~α(x);
4)Если α(x)~β
(x)
и β
(x)~γ(x),
то α(x)~γ(x);
5)Если α(x)~β
(x),
то и α(x)-β
(x)=о
(α(x))=о(β
(x));
6)Если α(x)~
α'(x)
и β
(x)~
β'(x),
то lim
β
(x)/
α(x)=
lim
β'(x)/
α'(x)
(x→a);
Функция y=β(x)
бесконечно
большая
при x→a,
если lim
β
(x)=бесконеч.
или lim
|β
(x)|=+бесконеч.
Свойства
ббф:1.
Если в некоторой прокол.окрестности
точки а
функция
α(x)≠0
и является бмф
при x→a,
то β
(x)=1/
α(x)
есть ббф
при x→a
и наоборот; 2)Произведение ббф
на функцию |f(x)|
>M≠0
есть ббф;
3)Сумма бесконечно большой и ограниченной
ф-ции есть ббф;
4)Сумма двух ббф
одинакого знака есть ббф.
8.
Сравнение
бесконечно малых ф-ций
производится путем нахождения предела
их отношений. Пусть α(x)
и β
(x)
– бмф
при
x→a,
причем lim
β
(x)/
α(x)=А.Тогда
если 1)А=1, то α(x)
и β
(x)
называются эквивалентными
бмф при
x→a,
что записывается в виде α(x)~β
(x);
2)А ≠0 и А=бесконеч., то α(x)
и β
(x)
– бмф
одного порядка малости
при x→a;
3)А=0, то β
(x)
есть бмф
более высокого порядка малости,
чем α(x),
при x→a,
что записывается в виде β
(x)=
о(α(x));
4)А=бесконеч., то α(x)
есть бмф более высокого порядка малости,
чем β
(x),
при x→a,
что записывается в виде α(x)=о(β
(x)).При
решении пределов
использование эквивалентных бесконечно
малых ф-ций в произведениях и частном.
При нахождении пределов бесконечно
малые множители, стоящие в числителе и
знаменателе заменяются им эквивалентными:
lim
f
(x)*p(x)/
g(x)=
lim
α (x)*γ(x)/
β(x),
если f
(x)
~α(x),
g(x)
~ β
(x),
p(x)
~ γ(x).9.
Основные теоремы о пределах. 1)теорема
о конечном пределе limf(x)=b↔f(x)=b+α(x)
при x→a;
2)теорема о связи с одностор.пределами:
limf(x)=b↔f(a-0)=f(a+0)=b
при x→a;
3)арифм.операции над пределами: умножение
на число: {xn}∙c={x1∙c,x2∙c..};
сложение и вычитание: {xn}±{yn}={x1±y1,
x2±y2..};
умножение и деление(если знаменатель
не равен 0) {xn}∙{yn}={x1∙y1,
x2∙y2..}
и {xn}/{yn}={x1/y1,
x2/y2..}
10.
Первый
зам. предел
limx->0(sinX)/X=1
используется для неопределенностей
вида [0/0] содержащих тригонометр. функции
. Пример:
Limx->0(tgX)/X=
Limx->0(sinX)/(X*CosX)=Limx->0sinX/X*Limx->01/cosX=[1/1]=1
Табл.
Эквивалентности: sinX=X;
tgX=X;
arcsinX=X;
arctgX=X;
1-cosX=X2/2;
cos2X=1-2sin2X
11.
Второй
зам. предел
limx->беск.(1+1/х)х=
Limx->0(1+х)1/х=е
используется для неопределенностей
вида [1беск.]
. Пример:
Limx->0(ln(x+4)-ln4)/x=
Limx->0(ln(x+4)/4)/x=1/4*Limx->0(ln(1+x/4))/(x/4)=1/4
Табл.
Эквивалентности: ex-1=x;
ln(1+x)=x;
ax-1=x*lna;
loga(1+x)=x*logae;
ln(x+√(x+1))=x;
(1+x)2-1=2x;
√(1+x)-1=x/2
12.
Определение
непрерывности ф-ции в точке. Ф-ция
y=f(x)
непрерывна в точке x0,если
f(x)
определена в точке x0
и
некоторой ее окрестности и limf(x)=f(x0)
при x→x0
13.Условие
непрерывности f(x)
непрерывна при x=x0
только в том случае, если 1)ф-ция определена
в точке x0;
2)если f(x0-0)f(x0+0)=f(x0)
Классификация
точек разрыва
Точки
разрыва 1 рода:1)т-ка устранимого разрыва
limf(x0-0)=limf(x0+0)=KєR,
f(x0)≠K
2)т-ка конечного скачка limf(x0-0)≠limf(x0+0)
Точки разрыва 2 рода 1)т-ка бесконечного
скачка: если оба предела существуют и
хотя бы 1 равен бесконечн.; 2)т-ка не
существования: если хотя бы один предел
не существует.
Все элементарные функции являются
непрерывными
в любой точке свой области определения.
14.
Свойства
функций, непрерывных на замкнутом
промежутке, и применение при исследовании
уравнений и неравенств.Если
функция f непрерывна
в замкнутой и ограниченной области Ω,
то:1)
функция f ограничена
на Ω ,
то есть существует такая постоянная M ,
что |f(x)|≤M при
всех xєΩ ;2)
функция f принимает
в области Ω наибольшее
и наименьшее значения, то есть существуют
такие точки x1єΩ и x2єΩ ,
что при всех xєΩ выполняются
неравенства f(x)≥f(x1) и.
f(x)≥f(x2) (В
этом случае точка x1 называется точкой
минимума,
а точка x2 -- точкой
максимума функции f в
области Ω .) 15.Производная
и её связь с дифференциалом, геом и
механ смысл производной и
дифференциала.Производной функции y = f ( x )
в точке x0 называется
предел:![]() для
любых двух точек A и B графика
функции:
для
любых двух точек A и B графика
функции: ![]() где
где ![]() - угол
наклона секущей AB.
производная
функции в точке есть угловой коэффициент
касательной к графику этой функции в
этой точке
-геометрический смысл производной.
В общем
случае уравнение прямой с угловым
коэффициентом f ’( x0 )
имеет вид:
y = f ’( x0 ) · x
+ b . Чтобы
найти b, воспользуемся
тем, что касательная проходит через
точку A:
f ( x0 )
= f ’( x0 ) · x0 +
b ,
отсюда, b = f ( x0 )
– f ’( x0 ) · x0 , и
подставляя это выражение вместо b,
мы получим уравнение
касательной:
y =
f ( x0 )
+ f ’( x0 ) · ( x
– x0 )
. Механический
смысл производной. Рассмотрим
простейший случай: движение материальной
точки вдоль координатной оси, причём
закон движения задан: координата x
движущейся точки – известная
функция x ( t )
времени t.
В течение
интервала времени от t0
до t0 +
- угол
наклона секущей AB.
производная
функции в точке есть угловой коэффициент
касательной к графику этой функции в
этой точке
-геометрический смысл производной.
В общем
случае уравнение прямой с угловым
коэффициентом f ’( x0 )
имеет вид:
y = f ’( x0 ) · x
+ b . Чтобы
найти b, воспользуемся
тем, что касательная проходит через
точку A:
f ( x0 )
= f ’( x0 ) · x0 +
b ,
отсюда, b = f ( x0 )
– f ’( x0 ) · x0 , и
подставляя это выражение вместо b,
мы получим уравнение
касательной:
y =
f ( x0 )
+ f ’( x0 ) · ( x
– x0 )
. Механический
смысл производной. Рассмотрим
простейший случай: движение материальной
точки вдоль координатной оси, причём
закон движения задан: координата x
движущейся точки – известная
функция x ( t )
времени t.
В течение
интервала времени от t0
до t0 + ![]() точка
перемещается на расстояние: x ( t0 +
точка
перемещается на расстояние: x ( t0 + ![]() ) - x ( t0 )
=
) - x ( t0 )
= ![]() ,
а её средняя
скорость равна: va =
,
а её средняя
скорость равна: va = ![]() /
/ ![]() . При
. При ![]()
![]() 0
значение средней скорости стремится к
определённой величине, которая
называется мгновенной
скоростью v ( t0 )
материальной точки в момент времени t0 .
Но по определению производной мы имеем:
0
значение средней скорости стремится к
определённой величине, которая
называется мгновенной
скоростью v ( t0 )
материальной точки в момент времени t0 .
Но по определению производной мы имеем:
![]() отсюда,
v ( t0 ) =x’ ( t0 ), т.e. скорость
– это производная координаты по времени. В
этом и состоит механический
смысл производной.Аналогично, ускорение
– это производная скорости по
времени: a = v’ ( t ).
16.
Уравнение
касательной.
Уравнение касательной к графику функции
y=f(x)
в точке х0
имеет
вид y=f(x0)+f’(x0)(x-x0),
где f’(x0)
– угловой коэффициент касательной.
Линеаризация
и ее геометрический смысл.
Лионариз. ф-ции-замена ф-ции у=f(x)
по х ф-цией y=f(x0)+f’(x0)(x-x0),что
геометрически соответствует замене
участка кривой у=f(x),примыкающего
к точке (х0;
f(x0)),отрезком
касательной и кривой в этой точке.17.
Дифференцируемость
ф-ции.
Функция
y=f(x) называется дифференцируемой в точке
x0,
если ее приращение Δy в точке x0
может быть представлено в виде:
Δy=A·Δx+α(Δx)·Δx, где A - некоторое число,
независящее от Δx, а α(Δx)- бесконечно
малая ф-ия от переменной Δx. Связь
дифференцируемости и непрерывности
ф-ции. Если
ф-ция дифференцируема в данной точке,
то она непрерывна в ней. Обратное
утверждение неверно, т.е. если ф-ция
непрерывна в точке, то она может быть
не дифференцируема в этой точке.
18(19,20).
Основные правила дифференцирования.
Пусть u=u(x)
и v=v(x)-
дифференцированные функции с независимой
переменной х; с=const.
Тогда: (c)’=0;
(x)’=1;
(u±v)’=u’±v’;
(u∙v)’=u’v+uv’;
(cu)’=cu’;
(u/v)’=(u’v-uv’)/v2;
где v=v(x)≠0.
Таблица
производных.
отсюда,
v ( t0 ) =x’ ( t0 ), т.e. скорость
– это производная координаты по времени. В
этом и состоит механический
смысл производной.Аналогично, ускорение
– это производная скорости по
времени: a = v’ ( t ).
16.
Уравнение
касательной.
Уравнение касательной к графику функции
y=f(x)
в точке х0
имеет
вид y=f(x0)+f’(x0)(x-x0),
где f’(x0)
– угловой коэффициент касательной.
Линеаризация
и ее геометрический смысл.
Лионариз. ф-ции-замена ф-ции у=f(x)
по х ф-цией y=f(x0)+f’(x0)(x-x0),что
геометрически соответствует замене
участка кривой у=f(x),примыкающего
к точке (х0;
f(x0)),отрезком
касательной и кривой в этой точке.17.
Дифференцируемость
ф-ции.
Функция
y=f(x) называется дифференцируемой в точке
x0,
если ее приращение Δy в точке x0
может быть представлено в виде:
Δy=A·Δx+α(Δx)·Δx, где A - некоторое число,
независящее от Δx, а α(Δx)- бесконечно
малая ф-ия от переменной Δx. Связь
дифференцируемости и непрерывности
ф-ции. Если
ф-ция дифференцируема в данной точке,
то она непрерывна в ней. Обратное
утверждение неверно, т.е. если ф-ция
непрерывна в точке, то она может быть
не дифференцируема в этой точке.
18(19,20).
Основные правила дифференцирования.
Пусть u=u(x)
и v=v(x)-
дифференцированные функции с независимой
переменной х; с=const.
Тогда: (c)’=0;
(x)’=1;
(u±v)’=u’±v’;
(u∙v)’=u’v+uv’;
(cu)’=cu’;
(u/v)’=(u’v-uv’)/v2;
где v=v(x)≠0.
Таблица
производных.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
Логарифмическое
дифференцирование.
Логар. диффер. называется метод диффер.
ф-ций, при котором сначала находится
логарифм функции, а затем вычисляется
производная от него. 22.
Неявно
заданная ф-ция.Под
неявным заданной функцией понимают
задание функции в виде уравнения
F(x;y)=0, не разрешенного относительно у.
Всякую явно заданную функцию у=ƒ (х)
можно записать как неявно заданную
уравнением ƒ(х)-у=0, но не наоборот. Не
всегда легко, а иногда и невозможно
разрешить уравнение относительно у
(например, у+2х+cosy-1=0 или 2у-х+у=0). Если
неявная функция задана уравнением F(x;
у)=0, то для нахождения производной от у
по х нет необходимости разрешать
уравнение относительно у: достаточно
продифференцировать это уравнение по
x, рассматривая при этом у как функцию
х, и полученное затем уравнение разрешить
относительно у'.Производная неявной
функции выражается через аргумент х и
функцию у. Параметрически
заданная ф-ция.Если
функция f задана параметрическиx = φ(t),
y = ψ(t), α < t < β,где y = f(x) и функции φ и
ψ дифференцируемы, причем φ'(t) ≠ 0, то
.
Логарифмическое
дифференцирование.
Логар. диффер. называется метод диффер.
ф-ций, при котором сначала находится
логарифм функции, а затем вычисляется
производная от него. 22.
Неявно
заданная ф-ция.Под
неявным заданной функцией понимают
задание функции в виде уравнения
F(x;y)=0, не разрешенного относительно у.
Всякую явно заданную функцию у=ƒ (х)
можно записать как неявно заданную
уравнением ƒ(х)-у=0, но не наоборот. Не
всегда легко, а иногда и невозможно
разрешить уравнение относительно у
(например, у+2х+cosy-1=0 или 2у-х+у=0). Если
неявная функция задана уравнением F(x;
у)=0, то для нахождения производной от у
по х нет необходимости разрешать
уравнение относительно у: достаточно
продифференцировать это уравнение по
x, рассматривая при этом у как функцию
х, и полученное затем уравнение разрешить
относительно у'.Производная неявной
функции выражается через аргумент х и
функцию у. Параметрически
заданная ф-ция.Если
функция f задана параметрическиx = φ(t),
y = ψ(t), α < t < β,где y = f(x) и функции φ и
ψ дифференцируемы, причем φ'(t) ≠ 0, то
![]() 24.
свойства
диффереренциалов.
dc
= 0, с = const.
d(u+v)=du
+ dv;
d(u+c)
= du
(c=
const);
d(uv)
= udv
+ vdu.;
d(cu)
= cdu
(с = const).
Свойство независимости вида дифференциала
от выбора независимой переменной
(инвариантность формы дифференциала):
дифференциал функции равен произведению
производной дифференциал аргументанезависимого
от того, является ли этот аргумент
независимой переменной или функцией
другой независимой переменной.
инвариантность
формы первого дифференциалаПусть
задана сложная функция y=F(t)=f(g(t)), y=f(x),
x=g(t).dy=(f(g(t))¢ dt=f¢(x)g¢(t)dt=f¢(x)dg=f¢(x)dx. Вид
первого дифференциала такой же, как и
в случае, когда x является независимой
переменной. Это свойство называется
свойством инвариантности дифференциала
первого порядка.25.
Производные
и дифференциалы высших порядков.Пусть
производная некоторой функции f
дифференцируема. Тогда производная от
производной этой функции называется
второй производной функции f и обозначается
f". Таким образом, f"(x) = (f'(x))'.26
великая
т. Ферма.Для
любого натурального числа n > 2 уравнение
an+bn=cn
имеет натуральных решений a, b и
c.27.т.Ролля.
если ординаты обоих концов гладкой
кривой равны, то на кривой найдется
точка, в которой касательная к кривой
параллельна оси абсцисс.28.т.
Лагранжа. Пусть
ф-ция у=f(x)
непрерывна на отрезке [a;b],дифференцируема
на интервале (а;в). Тогда существует
хотябы одна точка с предадлежит (а,в)
такая, что f(b)-f(a)=f’(c)(b-a)т.Коши
Пусть ф-ия f(х)
и g(x)
непрерывны на отрезке [a;b],дифференцируемы
на интервале (а,в) и g’(x)≠0
на интервале (а,в).Тогда существует
хотябы одна точка с пренадлежит
(а,в)такая, что
24.
свойства
диффереренциалов.
dc
= 0, с = const.
d(u+v)=du
+ dv;
d(u+c)
= du
(c=
const);
d(uv)
= udv
+ vdu.;
d(cu)
= cdu
(с = const).
Свойство независимости вида дифференциала
от выбора независимой переменной
(инвариантность формы дифференциала):
дифференциал функции равен произведению
производной дифференциал аргументанезависимого
от того, является ли этот аргумент
независимой переменной или функцией
другой независимой переменной.
инвариантность
формы первого дифференциалаПусть
задана сложная функция y=F(t)=f(g(t)), y=f(x),
x=g(t).dy=(f(g(t))¢ dt=f¢(x)g¢(t)dt=f¢(x)dg=f¢(x)dx. Вид
первого дифференциала такой же, как и
в случае, когда x является независимой
переменной. Это свойство называется
свойством инвариантности дифференциала
первого порядка.25.
Производные
и дифференциалы высших порядков.Пусть
производная некоторой функции f
дифференцируема. Тогда производная от
производной этой функции называется
второй производной функции f и обозначается
f". Таким образом, f"(x) = (f'(x))'.26
великая
т. Ферма.Для
любого натурального числа n > 2 уравнение
an+bn=cn
имеет натуральных решений a, b и
c.27.т.Ролля.
если ординаты обоих концов гладкой
кривой равны, то на кривой найдется
точка, в которой касательная к кривой
параллельна оси абсцисс.28.т.
Лагранжа. Пусть
ф-ция у=f(x)
непрерывна на отрезке [a;b],дифференцируема
на интервале (а;в). Тогда существует
хотябы одна точка с предадлежит (а,в)
такая, что f(b)-f(a)=f’(c)(b-a)т.Коши
Пусть ф-ия f(х)
и g(x)
непрерывны на отрезке [a;b],дифференцируемы
на интервале (а,в) и g’(x)≠0
на интервале (а,в).Тогда существует
хотябы одна точка с пренадлежит
(а,в)такая, что
![]() 29.
правило
Лопиталя
Пусть функции f(x) и g(x) дифференцируемы
в некоторой окрестности точки a, за
исключением, быть может, самой точки a,
и пусть limf(x)=limg(x)=0
при x→a
или limf(x)=limg(x)=бесконечн.
Тогда, если существует предел отношения
производных этих функций lim(f’(x)/g’(x))
при x→a,
то существует и предел отношения самих
функций lim(f(x)/g(x))
при x→а, причем они равны.
32.Услов.монотонности.Для
того чтобы дифференц-ая на интервале(a,b)ф-ция
y=f(x)
не убывала(не возрастала)на этом
интервале,необходимо и достаточно,чтоб
ее производная была во всех точках
интервала неотрицат-ой,т.е f΄(x)≥0
(неположит-ой,т.е f΄(x)≤0.Если
во всех точк. интервала(a,b)
f΄(x)>0
(f΄(x)<0)то
ф-ция возрастает (убывает)на
интервале(a,b).33.Локальные
экстремумы ф-ции.
Т-ка х0
назыв.т-кой локал-го максим.(миним-ма)
если сущ такая окрест-ть точки х,что для
всех т-ек х≠ х0
из этой окрестности выполн-ся неравенство
f(x)≤f(х0)(соотв-но
f(x)≥f(х0))Если
в окрест-ти т-ки х0
для всех т-ек х≠х0
выполн-ся нерав-во f(x)<f(х0)
(соотв-но f(x)>(
х0)),то
т-ка х0
назыв.т-кой строгого локал-ого
максим.(миним.). Необходимое
условие экстремума.Если
ф-ция y=f(x)имеет
в т-ке х0
экстремумто производная в этой т-ке=0
или не сущ.Т-ки обл.определения ф-ции
y=f(x)
в котор ее производная=0или не
сущ.,назыв.критическими точк. ф-ции.Ф-ция
может иметь экстремум только в критич-их
т-ках.34Достаточное
условие сущ.локал. экстремума по первой
производной
Пусть ф-ция y=f(x)
непрерывна в т-ке х0
и
дифференц-ма в некотор. ее окрестности
,за исключен.самой т-ки х0
.
Тогда
если при переходе слква направо через
т-ку х0.
Производная
меняет знак с – на +,то х0.
явл.
т-кой сторогого миним.,если знак меняется
с + на - ,то т-ка х0.
явл.
т-кой строгого максим. Правила(1-ое
и 2-ое) нахождения локальных экстремумов
ф-ции по высшим порядкам
1-ое (по перв произв-ой):1.находим обл.
определен. ф-ции y=f(x)
и интервалы непрерывности.2.находим
критические т-кии наносим на
прямую.4.определяем знак производной в
каждом из полученных интервалов-если
производн. >0,то это интервал строгого
возрастания,если <0 то интервал строгого
убывания.5.устанавливаем как меняется
знак производной в окрестности
кажд.критич.т-ки-если при переходе слева
направо через т-ку х0.
Производн.меняет
знак с – на +,то х0.
явл
т-кой строгого миним.,если с + на -,то х0
т-ка
строгого максим.6.вычмсляем значен.
ф-ции(экстремумы) в т-ках макс.и
миним.,строим эскиз графикав окрестности
кажд критич. т-ки2-ое(по второй
произв.):1.находим перв производ. f΄(x)
и т-ки в котор она =нулю.2.находим втоорую
производн. f΄΄(x)
и определяем ее знак в кажд стациопарн
т-ке х0.
Если
f΄΄(x)<0,то
х0.
т-кастрогого
максим. Если f΄΄(x)>0,то х0.
т-ка
строгого миним.В случае f΄΄(x)= можно
воспользоваться перв правилом.35.Нахождение
наибол. и наименьш значен ф-ции на замкнут
промежутке.1)находим
критические т-ки ф-ции y=f(x)
принадлежащ интервалу(а,b).2)вычисляем
значения ф-ции в критич точк.и на концах
отрезка.3)из получ-ых знач-ий выбираем
наибольш и наменьш.36.Выпукл.
и вогнут. ф-ции,их св-ва. Ф-ция y=f(
выпуклой(вогнутой) на интервале (а,b)
если любая дугаее графика(отвечающ-го
этому интервалу расположена не выше(не
ниже)стягивающей дугу хорды.Дифферен-мая
ф-ция выпукла(вогнута)на интервале если
ее график расположен не ниже(не выше)дюбой
касательной к нему. Условие
выпуклости(вогнутости).Если
вторая производная f΄´(x)≥0
(f΄΄(x)≤0)
во всех т-ках интервала(а,b),то
ф-ция y=f(x)
выпукла(вогнута) на этом интервале.Если
эти нерав-ва строгие то и
выпуклость(вогнутость)будет строгая.37.Точки
перегиба.—т-ки
непрерывности ф-ции,в котор меняется
выпуклость на вогнутость или наоборот.Если
х0
т-ка перегиба ф-ции y=f(x),то
т-ка(х0
;f(х0
))назыв т-кой перегиба графига этой
ф-ции.
Праила нахождения т-кек перегиба
1.находим
обл определен ф-ции.2.находим вторую
производную f''(x)
ф-ции и т-ки обл определения,в котор
вторая производн =0или не сущ.отмечаем
их на числовой прямой3.определ. знак
второй производной в кажд интервалеесли.если
в рассматрив-ом интервале f''(x)<0то
в этом интервале ф-ция
вогнута,еслю>0-выпукла.4.среди т-ек,в
котр ф-ция непрерывна а вторая производн=0
или не сущ.,определяем те при переходе
через которые вторая производная меняет
знак. эти т-ки явл.т-ами перегиба.деляем
38Асимптота
графика ф-ции.
—прямая расстояние от котор до т-ки
лежащей на кривой стремится к 0 при
неогранич-ом удалении от начала координат
этой т-ки по кривой. Вертик.ассимптота.
графика ф-ции y=f(x)—прямая
х=а если хотя бы один из односторон-х
пределов в т-ке х=а равен +∞(или
-∞).Наклонная асс-та —прямая y=kx+b,
если
29.
правило
Лопиталя
Пусть функции f(x) и g(x) дифференцируемы
в некоторой окрестности точки a, за
исключением, быть может, самой точки a,
и пусть limf(x)=limg(x)=0
при x→a
или limf(x)=limg(x)=бесконечн.
Тогда, если существует предел отношения
производных этих функций lim(f’(x)/g’(x))
при x→a,
то существует и предел отношения самих
функций lim(f(x)/g(x))
при x→а, причем они равны.
32.Услов.монотонности.Для
того чтобы дифференц-ая на интервале(a,b)ф-ция
y=f(x)
не убывала(не возрастала)на этом
интервале,необходимо и достаточно,чтоб
ее производная была во всех точках
интервала неотрицат-ой,т.е f΄(x)≥0
(неположит-ой,т.е f΄(x)≤0.Если
во всех точк. интервала(a,b)
f΄(x)>0
(f΄(x)<0)то
ф-ция возрастает (убывает)на
интервале(a,b).33.Локальные
экстремумы ф-ции.
Т-ка х0
назыв.т-кой локал-го максим.(миним-ма)
если сущ такая окрест-ть точки х,что для
всех т-ек х≠ х0
из этой окрестности выполн-ся неравенство
f(x)≤f(х0)(соотв-но
f(x)≥f(х0))Если
в окрест-ти т-ки х0
для всех т-ек х≠х0
выполн-ся нерав-во f(x)<f(х0)
(соотв-но f(x)>(
х0)),то
т-ка х0
назыв.т-кой строгого локал-ого
максим.(миним.). Необходимое
условие экстремума.Если
ф-ция y=f(x)имеет
в т-ке х0
экстремумто производная в этой т-ке=0
или не сущ.Т-ки обл.определения ф-ции
y=f(x)
в котор ее производная=0или не
сущ.,назыв.критическими точк. ф-ции.Ф-ция
может иметь экстремум только в критич-их
т-ках.34Достаточное
условие сущ.локал. экстремума по первой
производной
Пусть ф-ция y=f(x)
непрерывна в т-ке х0
и
дифференц-ма в некотор. ее окрестности
,за исключен.самой т-ки х0
.
Тогда
если при переходе слква направо через
т-ку х0.
Производная
меняет знак с – на +,то х0.
явл.
т-кой сторогого миним.,если знак меняется
с + на - ,то т-ка х0.
явл.
т-кой строгого максим. Правила(1-ое
и 2-ое) нахождения локальных экстремумов
ф-ции по высшим порядкам
1-ое (по перв произв-ой):1.находим обл.
определен. ф-ции y=f(x)
и интервалы непрерывности.2.находим
критические т-кии наносим на
прямую.4.определяем знак производной в
каждом из полученных интервалов-если
производн. >0,то это интервал строгого
возрастания,если <0 то интервал строгого
убывания.5.устанавливаем как меняется
знак производной в окрестности
кажд.критич.т-ки-если при переходе слева
направо через т-ку х0.
Производн.меняет
знак с – на +,то х0.
явл
т-кой строгого миним.,если с + на -,то х0
т-ка
строгого максим.6.вычмсляем значен.
ф-ции(экстремумы) в т-ках макс.и
миним.,строим эскиз графикав окрестности
кажд критич. т-ки2-ое(по второй
произв.):1.находим перв производ. f΄(x)
и т-ки в котор она =нулю.2.находим втоорую
производн. f΄΄(x)
и определяем ее знак в кажд стациопарн
т-ке х0.
Если
f΄΄(x)<0,то
х0.
т-кастрогого
максим. Если f΄΄(x)>0,то х0.
т-ка
строгого миним.В случае f΄΄(x)= можно
воспользоваться перв правилом.35.Нахождение
наибол. и наименьш значен ф-ции на замкнут
промежутке.1)находим
критические т-ки ф-ции y=f(x)
принадлежащ интервалу(а,b).2)вычисляем
значения ф-ции в критич точк.и на концах
отрезка.3)из получ-ых знач-ий выбираем
наибольш и наменьш.36.Выпукл.
и вогнут. ф-ции,их св-ва. Ф-ция y=f(
выпуклой(вогнутой) на интервале (а,b)
если любая дугаее графика(отвечающ-го
этому интервалу расположена не выше(не
ниже)стягивающей дугу хорды.Дифферен-мая
ф-ция выпукла(вогнута)на интервале если
ее график расположен не ниже(не выше)дюбой
касательной к нему. Условие
выпуклости(вогнутости).Если
вторая производная f΄´(x)≥0
(f΄΄(x)≤0)
во всех т-ках интервала(а,b),то
ф-ция y=f(x)
выпукла(вогнута) на этом интервале.Если
эти нерав-ва строгие то и
выпуклость(вогнутость)будет строгая.37.Точки
перегиба.—т-ки
непрерывности ф-ции,в котор меняется
выпуклость на вогнутость или наоборот.Если
х0
т-ка перегиба ф-ции y=f(x),то
т-ка(х0
;f(х0
))назыв т-кой перегиба графига этой
ф-ции.
Праила нахождения т-кек перегиба
1.находим
обл определен ф-ции.2.находим вторую
производную f''(x)
ф-ции и т-ки обл определения,в котор
вторая производн =0или не сущ.отмечаем
их на числовой прямой3.определ. знак
второй производной в кажд интервалеесли.если
в рассматрив-ом интервале f''(x)<0то
в этом интервале ф-ция
вогнута,еслю>0-выпукла.4.среди т-ек,в
котр ф-ция непрерывна а вторая производн=0
или не сущ.,определяем те при переходе
через которые вторая производная меняет
знак. эти т-ки явл.т-ами перегиба.деляем
38Асимптота
графика ф-ции.
—прямая расстояние от котор до т-ки
лежащей на кривой стремится к 0 при
неогранич-ом удалении от начала координат
этой т-ки по кривой. Вертик.ассимптота.
графика ф-ции y=f(x)—прямая
х=а если хотя бы один из односторон-х
пределов в т-ке х=а равен +∞(или
-∞).Наклонная асс-та —прямая y=kx+b,
если
![]() ,что
равносильно сущ-нию конечн.пределов
,что
равносильно сущ-нию конечн.пределов
![]()
![]() .Если
k=0,то
.Если
k=0,то
![]() .Поэтому
y=b—уравнение
горизонт. асимпт(она частный случай
наклонной асимпт.)39Общ.
схема исследов-я ф-ции и
построен.граф.1)предварительное
исследов-е зависимости y=f(x).2)исследов.по
первой производной.3)исследован.по
второй производн.4)построен.схемы графика
с учетом получ-ых результ. Построение
графика.Iэтап:1.найти
обл определен.и интервалы непрерывности.2.если
есть т-ки разрыва найти односторон
пределы ф-ции в этих т-ках и изобразить
на чертеже поведение ф-ции вблизи
кажд.т-ки разрыва.3.исследовать ф-цию на
четность нечетночть переодичность.4.найти
ассимтоты 5.найти т-ки пересечения
графика с осями координат и отметить
их на граф.IIэтап:1.найти
первую производную f´(x)2.найти
критические т-ки (f´(x)=0
или не сущ)3.найти интервалы возрастания
(f´(x)>0)
и убывания (f΄(x)<0).4.найти
т-ки максим и миним,вычислить значения
ф-ции в этих т-ках ,изобр на
чертеже.IIIэтап:1.найти
вторую производную f´´(x).2.найти
промеж вогнутости (f´´(x)<0)
и выпукл-ти(f´´(x)>0).3.найти
т-ки перегиба(f´´(x)=0
или не сущ.,но в окрестности т-ки меняет
знак),вычислить поведен ф-ции в окрестности
этих т-к на чертеже.IVэтап:построение
графика с учетом всех данных.40.
Комплексное
число z-
число вида z=(a+bi),
где a
и b–
действительные числа,i
– так назыв мнимая единица. Число a
называется действительной частью (Re
z)
комплексного числа z,
число b
называется мнимой частью (Im
z)
комплексного числа z.Действия
над комплекс.числами в алгебр.форме.
Сложение, вычитание, умножение и
деление.Формы
записи компл чисел.
Тригонометрическая и показательная
Формула Муавра.
Zn=rn(cosnφ+i*sin
nφ)
41
Действия
над компл числами в тригонометр форме
Умножение,деление,
возведение в степень,извлечение корня
n-ой
степ.Показательная
форма компл числа.Всякое
компл число можно представить в так
нываем. показат.форме. z=reiφ
42Понятие
о ф-циях комплекс.переменной
.
Если
каждому комплексному числу , принадлежащему
области комплексной плоскости , поставлено
в соответствие некоторое комплексное
число , то говорят, что в области определена
комплексная ф-цияМножество
комплексных чисел , соответствующих
всем , назыв множеством
значений
43.Неопределенный
интеграл.Общ.вид
первообразных для ф-ции y=f(x) (на интервале
(a,b))назыв
неопределенным интегралом от этой ф-ции
(на интервале (a,b)) и обознач. ∫f(x)dx.Таким
обр. ∫f(x)dx= F(x)+C,x€(a,b).F(x)-произвол.первообразная
для f(x),C-произвол.постоянная.Св-ва.
1.Дифферен-ание обратно интегрированию
(∫f(x)dx)´=f(x),
d∫f(x)dx
=f(x)dx.2.Интегрирование обратно дифференц-анию.
∫f´
(x)dx=f(x)+C,
∫dF(x)=F(x)+C.3.Линейность:а)постоянный
множ-ль можно выносить за знак
интеграла.б)интеграл от
суммы(разности)интегрируемых ф-ций
=сумме(разности) интегралов этих
ф-ций.в)неопредел. интеграл от линейной
комбинации интегрируемых ф-ций =
соответств.линейной комбинации интегралов
от этих ф-ций.4.Св-во инвариантности
формул интегриров-ия:всякая формула
сохр.свой вид при замене независим.
переменной.
∫f(x)dx=F(x)+C→∫f(u)du=∫f(u(x))u'(x)dx=F(u(x))+C,где
u=u(x)-любая
непрерывно дифференц-ая ф-ция от х, в
частности ∫f(ax+b)dx=1/a*F(ax+b)+C,
где а≠0. 44.Непосредствонное
интегрирование—нахожден
интегралов с помощ. преобразований
подынтегрального выражения с использованием
основных св-в и табл. неопределенных
интегралов.Табл
Интегралов.45
Интегрирование
замены переменной.Этот
метод состоит в преобразовании интеграла
∫f(x)dx
в др.интеграл ∫g(u)du,метод
интегрирования которого известен,с
последующ.возвращением исходной
переменной.1)Интегриров подстановкой-вынесен
множ-ля из-под знака дифф-ла:Пусть ф-ция
y=f(x)
неперерывна на интервале Х,а ф-ция х=φ(t)
непрерывно дифферен-ма на интервале Т
и имеет непрерывно дифференц-мую обратную
функцию t=ψ(х) для х€Х.Пусть далее
G-первообразная для ф-ции g(t)=f(ψ(t))φ´(t)
на Т.Тогда f(x)
интегрируема на Х,причем
∫f(x)dx=G(ψ(x))+C.2)Внесение
множ-ля под знак дифф-ла:Пусть ф-ция
х=φ(t) со множ-вом значений Х имеет
непрерывн производную на интервале Т,а
ф-ция y=f(x),
непрерывна и имеет первообразную F(x)
на Х.Тогда ф-ция g(t)=f(ψ(t))φ´(t)
интегрируема на Т,причем
∫g(t)=f(φ(t))φ´(t)dt=F(φ(t))+C.
Пример.
Внесение:
f(x)dx=х=φ(t),t=
ψ(x)=∫f(φ(t))φ´(t)dt=∫g(t)dt=G(t)+C=G(ψ(x))+C.
Вынесение: ∫g(t)dt=∫f(φ(t))φ´(t)dt=
∫ f(x)dx=F(x)+C=F(φ(t))+C.46
Интегрирование
по частям Этот
метод основывается на формуле
дифференцирования произведения двух
ф-ций ∫udv=uv-∫vdu.
1
тип ∫Pn(x)sin(ax+b),cos(ax+b),eax+b
,
cax+b
dx
в этом случае Pn(x)-u,
остальное dv
2тип
∫Pn(x)arcsin(ax+b),arccos(ax+b),arctg(ax+b),arcctg(ax+b),ln(ax+b),logc(ax+b)
здесь Pn(x)dx-dv,
остальное u.
47.
Интегрирование
рацион.ф-ций
Рацион.ф-цией
назыв выражение вида Pn(x)/Qm(x),
где Pn(x)/Qm(x)-
многочлены, если n<m,
то дробь правильная, если n≥m,
то неправильная. x↔A/x;
xk↔A/x+B/x2…;
(ax+b)↔A/(ax+b);
(ax+b)k↔A/(ax+b)+B/(ax+b)2…;
(ax2+bx+c)↔(Ax+b)/(ax2+bx+c);
(ax2+bx+c)k↔(Ax+b)/(ax2+bx+c)+(Cx+D)/(ax2+bx+c)2…48.
Алгоритм
интегрирования рацион.ф-ций 1)Проверить
является ли дробь правильной, если нет,
то выделить целую часть, поделив числит.на
знаменат.уголком. 2)Разложить
заменат.правильной дроби на множители
вида: xk;
(ax+b)k;
(ax2+bx+c)k.
3)Разложить дробь на сумму простейших
дробей. 4)Определить коэф. А,В,С. 5)Вычислить
интегралы от каждой простейшей дроби.49.
Интегрирование
ф-ций, зависящ,от тригонометричсеских
Согласно
этому методу ищется подходящая замена
переменных. 1)Универс.тригонометр.подстановка
tg
x/2=t,
x=arctgt,
dx=2dt/(1+t2),
sinx=2t/(1+t2),
cosx=(1-t2)/(1+t2)
2)
Если sin
и cos
в четн.степени в числителе(знаменат.нет
) sin2x=(1-cos2x)/2
cos2x=(1+cos2x)/2
3)Использ.если
интеграл зависит от tg
или sin
и cos
в четн степени tgx=t,
x=arctgt,
dx
=dt/(1+t2).
52.Понятие
координаты. Связь с декартовыми
Можно установить связь между полярной
системой координат и декартовой
прямоугольной системой, если поместить
начало декартовой прямоугольной системы
в полюс, а полярную ось направить вдоль
положительного направления оси Ох. Тогда
координаты произвольной точки в двух
различных системах координат связываются
соотношениями: x
= rcosj;
y
= rsinj;
x2 +
y2 =
r2
53.
Матрицы.
Основные понятия и действия над матрицами.
Матрицей
размера
m×n
называется прямоугольная таблица чисел
(или других математичесиких объектов)
— элементов матрицы, расположенных в
m
строках и n
столбцах. aij—
элемент, принадлежащий и-й строке и
житому столбцу матрицы, числа i
j
называются индексами элемента. Действия
над матрицами: Суммой (разностью)
С=А+В (С=А-В) двух матриц называется такая
матрица, элементы которой равны
сумме(разности)соответствующих элементов
матриц. Складываются матрицы только
одинаковы размеров. Произведением
матрицы
на число альфа( или числа альфа на
матрицу) называется матрица, элементы
которой равны соответствующим элементам
матрицы А, умноженных на альфа С=
А*ʎ. 54.
Определители
второго и третьего порядка, их вычисление
и основные свойства. Определитель
2-го порядка
.Поэтому
y=b—уравнение
горизонт. асимпт(она частный случай
наклонной асимпт.)39Общ.
схема исследов-я ф-ции и
построен.граф.1)предварительное
исследов-е зависимости y=f(x).2)исследов.по
первой производной.3)исследован.по
второй производн.4)построен.схемы графика
с учетом получ-ых результ. Построение
графика.Iэтап:1.найти
обл определен.и интервалы непрерывности.2.если
есть т-ки разрыва найти односторон
пределы ф-ции в этих т-ках и изобразить
на чертеже поведение ф-ции вблизи
кажд.т-ки разрыва.3.исследовать ф-цию на
четность нечетночть переодичность.4.найти
ассимтоты 5.найти т-ки пересечения
графика с осями координат и отметить
их на граф.IIэтап:1.найти
первую производную f´(x)2.найти
критические т-ки (f´(x)=0
или не сущ)3.найти интервалы возрастания
(f´(x)>0)
и убывания (f΄(x)<0).4.найти
т-ки максим и миним,вычислить значения
ф-ции в этих т-ках ,изобр на
чертеже.IIIэтап:1.найти
вторую производную f´´(x).2.найти
промеж вогнутости (f´´(x)<0)
и выпукл-ти(f´´(x)>0).3.найти
т-ки перегиба(f´´(x)=0
или не сущ.,но в окрестности т-ки меняет
знак),вычислить поведен ф-ции в окрестности
этих т-к на чертеже.IVэтап:построение
графика с учетом всех данных.40.
Комплексное
число z-
число вида z=(a+bi),
где a
и b–
действительные числа,i
– так назыв мнимая единица. Число a
называется действительной частью (Re
z)
комплексного числа z,
число b
называется мнимой частью (Im
z)
комплексного числа z.Действия
над комплекс.числами в алгебр.форме.
Сложение, вычитание, умножение и
деление.Формы
записи компл чисел.
Тригонометрическая и показательная
Формула Муавра.
Zn=rn(cosnφ+i*sin
nφ)
41
Действия
над компл числами в тригонометр форме
Умножение,деление,
возведение в степень,извлечение корня
n-ой
степ.Показательная
форма компл числа.Всякое
компл число можно представить в так
нываем. показат.форме. z=reiφ
42Понятие
о ф-циях комплекс.переменной
.
Если
каждому комплексному числу , принадлежащему
области комплексной плоскости , поставлено
в соответствие некоторое комплексное
число , то говорят, что в области определена
комплексная ф-цияМножество
комплексных чисел , соответствующих
всем , назыв множеством
значений
43.Неопределенный
интеграл.Общ.вид
первообразных для ф-ции y=f(x) (на интервале
(a,b))назыв
неопределенным интегралом от этой ф-ции
(на интервале (a,b)) и обознач. ∫f(x)dx.Таким
обр. ∫f(x)dx= F(x)+C,x€(a,b).F(x)-произвол.первообразная
для f(x),C-произвол.постоянная.Св-ва.
1.Дифферен-ание обратно интегрированию
(∫f(x)dx)´=f(x),
d∫f(x)dx
=f(x)dx.2.Интегрирование обратно дифференц-анию.
∫f´
(x)dx=f(x)+C,
∫dF(x)=F(x)+C.3.Линейность:а)постоянный
множ-ль можно выносить за знак
интеграла.б)интеграл от
суммы(разности)интегрируемых ф-ций
=сумме(разности) интегралов этих
ф-ций.в)неопредел. интеграл от линейной
комбинации интегрируемых ф-ций =
соответств.линейной комбинации интегралов
от этих ф-ций.4.Св-во инвариантности
формул интегриров-ия:всякая формула
сохр.свой вид при замене независим.
переменной.
∫f(x)dx=F(x)+C→∫f(u)du=∫f(u(x))u'(x)dx=F(u(x))+C,где
u=u(x)-любая
непрерывно дифференц-ая ф-ция от х, в
частности ∫f(ax+b)dx=1/a*F(ax+b)+C,
где а≠0. 44.Непосредствонное
интегрирование—нахожден
интегралов с помощ. преобразований
подынтегрального выражения с использованием
основных св-в и табл. неопределенных
интегралов.Табл
Интегралов.45
Интегрирование
замены переменной.Этот
метод состоит в преобразовании интеграла
∫f(x)dx
в др.интеграл ∫g(u)du,метод
интегрирования которого известен,с
последующ.возвращением исходной
переменной.1)Интегриров подстановкой-вынесен
множ-ля из-под знака дифф-ла:Пусть ф-ция
y=f(x)
неперерывна на интервале Х,а ф-ция х=φ(t)
непрерывно дифферен-ма на интервале Т
и имеет непрерывно дифференц-мую обратную
функцию t=ψ(х) для х€Х.Пусть далее
G-первообразная для ф-ции g(t)=f(ψ(t))φ´(t)
на Т.Тогда f(x)
интегрируема на Х,причем
∫f(x)dx=G(ψ(x))+C.2)Внесение
множ-ля под знак дифф-ла:Пусть ф-ция
х=φ(t) со множ-вом значений Х имеет
непрерывн производную на интервале Т,а
ф-ция y=f(x),
непрерывна и имеет первообразную F(x)
на Х.Тогда ф-ция g(t)=f(ψ(t))φ´(t)
интегрируема на Т,причем
∫g(t)=f(φ(t))φ´(t)dt=F(φ(t))+C.
Пример.
Внесение:
f(x)dx=х=φ(t),t=
ψ(x)=∫f(φ(t))φ´(t)dt=∫g(t)dt=G(t)+C=G(ψ(x))+C.
Вынесение: ∫g(t)dt=∫f(φ(t))φ´(t)dt=
∫ f(x)dx=F(x)+C=F(φ(t))+C.46
Интегрирование
по частям Этот
метод основывается на формуле
дифференцирования произведения двух
ф-ций ∫udv=uv-∫vdu.
1
тип ∫Pn(x)sin(ax+b),cos(ax+b),eax+b
,
cax+b
dx
в этом случае Pn(x)-u,
остальное dv
2тип
∫Pn(x)arcsin(ax+b),arccos(ax+b),arctg(ax+b),arcctg(ax+b),ln(ax+b),logc(ax+b)
здесь Pn(x)dx-dv,
остальное u.
47.
Интегрирование
рацион.ф-ций
Рацион.ф-цией
назыв выражение вида Pn(x)/Qm(x),
где Pn(x)/Qm(x)-
многочлены, если n<m,
то дробь правильная, если n≥m,
то неправильная. x↔A/x;
xk↔A/x+B/x2…;
(ax+b)↔A/(ax+b);
(ax+b)k↔A/(ax+b)+B/(ax+b)2…;
(ax2+bx+c)↔(Ax+b)/(ax2+bx+c);
(ax2+bx+c)k↔(Ax+b)/(ax2+bx+c)+(Cx+D)/(ax2+bx+c)2…48.
Алгоритм
интегрирования рацион.ф-ций 1)Проверить
является ли дробь правильной, если нет,
то выделить целую часть, поделив числит.на
знаменат.уголком. 2)Разложить
заменат.правильной дроби на множители
вида: xk;
(ax+b)k;
(ax2+bx+c)k.
3)Разложить дробь на сумму простейших
дробей. 4)Определить коэф. А,В,С. 5)Вычислить
интегралы от каждой простейшей дроби.49.
Интегрирование
ф-ций, зависящ,от тригонометричсеских
Согласно
этому методу ищется подходящая замена
переменных. 1)Универс.тригонометр.подстановка
tg
x/2=t,
x=arctgt,
dx=2dt/(1+t2),
sinx=2t/(1+t2),
cosx=(1-t2)/(1+t2)
2)
Если sin
и cos
в четн.степени в числителе(знаменат.нет
) sin2x=(1-cos2x)/2
cos2x=(1+cos2x)/2
3)Использ.если
интеграл зависит от tg
или sin
и cos
в четн степени tgx=t,
x=arctgt,
dx
=dt/(1+t2).
52.Понятие
координаты. Связь с декартовыми
Можно установить связь между полярной
системой координат и декартовой
прямоугольной системой, если поместить
начало декартовой прямоугольной системы
в полюс, а полярную ось направить вдоль
положительного направления оси Ох. Тогда
координаты произвольной точки в двух
различных системах координат связываются
соотношениями: x
= rcosj;
y
= rsinj;
x2 +
y2 =
r2
53.
Матрицы.
Основные понятия и действия над матрицами.
Матрицей
размера
m×n
называется прямоугольная таблица чисел
(или других математичесиких объектов)
— элементов матрицы, расположенных в
m
строках и n
столбцах. aij—
элемент, принадлежащий и-й строке и
житому столбцу матрицы, числа i
j
называются индексами элемента. Действия
над матрицами: Суммой (разностью)
С=А+В (С=А-В) двух матриц называется такая
матрица, элементы которой равны
сумме(разности)соответствующих элементов
матриц. Складываются матрицы только
одинаковы размеров. Произведением
матрицы
на число альфа( или числа альфа на
матрицу) называется матрица, элементы
которой равны соответствующим элементам
матрицы А, умноженных на альфа С=
А*ʎ. 54.
Определители
второго и третьего порядка, их вычисление
и основные свойства. Определитель
2-го порядка
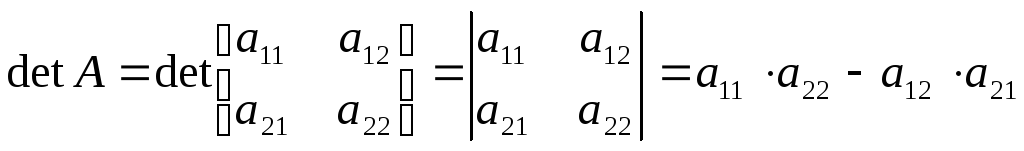 Опеределители
3-го порядка
Опеределители
3-го порядка
