^	^
при фиксированных X и	Ψ , соответствующих экстремуму, и соблюдении ус-
ловий трансверсальности.
Обычно область С определяется неравенствами вида:
uj		≤ uj	≤ uj	, j=1,2,...,r.
min			max

Оптимальное управление на основе (24.11) может быть получено в сле- дующих вариантах:

- как локальный экстремум внутри области C в соответствии с условиями

(24.7);

		^	= uj
	- как абсолютный экстремум на границе области С ( u j			или
^			min
	= uj
u j		);
	max

- как кусочно-непрерывная функция, на отдельных временных интервалах совпадающая с границами, а на других - принимающая значения внутри облас- ти C.

В последнем случае для точек разрыва управления (при t=t*) следует

учитывать недопустимость скачкообразного изменения переменных состояния объекта управления:

x i (t*+0 ) = x i (t*−0 ), i=1,2,...n ;	(24.12)
и условия Вейерштрассе-Эрдмана:
ψ i (t*+0 ) = ψ i (t*−0 ), i=1,2,...n; H (t*+0 ) = H (t*−0 ).	(24.13)

В заключение отметим, что для достижения максимума функционала (24.2) потребуется достижение минимума функции Гамильтона. Кроме того,

аналогичный принцип может быть сформулирован и использован для функции Лагранжа (принцип минимума).

Лекция 25. Синтез системы стабилизации, оптимальной по быстродействию

Расссмотрим линейный объект управления, описываемый системой урав- нений (23.1). Требуется определить программу управления U(t)=(u1(t), u2(t),..., ur(t)) и построить контур управления, обеспечивающие стабилизацию объекта управления за минимальное время T. Граничные условия фиксирован-

ные: xi(0)=xi0, i=1,2,...,n;					. Заданы ограни-
чения на управление:		uj		≤ ujmax , j=1,2,...,r.	(25.1)

Оптимизированный функционал вводится в рассматриваемой задаче сле- дующим образом:

91

T
J(X ,U ) = T = ò1× dt ® min .	(25.2)

0

Составим функцию Гамильтона:

n .

H = -1 + åyi x i

i=1

n	æ	n
= -1 + åyi çç		åaij x j
i=1	è j=1

r

+ å

l=1

ö

b u ÷ .

il l ÷ø

Рассмотрим сначала случай, когда есть одна составляющая сигнала управления:

n	.	n	æ	n	ö	n
H = -1 + åyi x i = -1		+ å	ççyi åaij x j ÷÷			+ uåyibi . (25.3)
i=1		i=1	è	j=1	ø	i=1

Поскольку в соответствии с принципом максимума все переменные, кро- ме u, в (25.2) принимаются фиксированными, при поиске оптимального управ- ления в (25.2) можно пренебречь всеми слагаемыми, не содержащими u:

n

u = arg max åyibi . i=1

Очевидно, что максимум такого выражения достигается при n

u(t) = umax signåbiyi (t), то есть оптимальное управление является релей-

i=1

ным с переключениями между двумя значениями:

при

u(t) = umin при

n

åbiyi (t) > 0 ,

i=1

n

åbiyi (t) < 0 .

i=1

Для случая векторного управления аналогично можно получить, что при ограничениях вида (20.1) каждая составляющая оптимального вектора управ- ления линейным объектом определяется соотношением:

n

uj (t) = ujmax signåbij yi (t). (25.4) i=1

Теорема об n интервалах (теорема Фельдбаума): если собственные числа матрицы A линейного объекта управления вещественные и область управления ограничена неравенствами вида (25.1), то каждая составляющая uj оптимально- го по быстродействию управления кусочно-постоянна и имеет не более n-1 пе- реключения между значениями ujmax и −u jmax , где n - порядок системы.

92

Кроме того, доказано, что для линейной системы, у которой все собст- венные числа матрицы A лежат в левой полуплоскости, всегда может быть оп- ределено оптимальное по быстродействию управление, если только границы допустимых значений всех составляющих управляющего сигнала имеют раз-

ный знак: signuj	= −signuj	min	.
max
Рассмотрим пример для объекта управления, описываемого системой
уравнений второго порядка:			.
			x 1	= x 2 ,
			.		= u
			x 2

при наличии ограничения u £ umax .

Требуется построить управление u=u(x1,x2), переводящее объект из произвольного заданного начального состояния (x10, x20) в состояние (0, 0) за

минимальное время T.
	Найдем собственные числа матрицы A. Для этого нужно решить уравне-
ние:		, где I - единичная матрица. Для заданного объекта урав-
нение
	примет вид:		l	-1
					= l2 = 0 .
			0	l

Собсвенные числа матрицы l1=l2=0. Порядок системы n=2. Следова- тельно, в соответствии с теоремой об n интервалах, оптимальное управление кусочно-постоянно и может иметь не более одного переключения. Возможные варианты управления:

1.u = umax , t Î[0,T ).

2.u = −umax , t Î[0,T ).

			ì umax		t Î[0,t)
	3. u = í-u				t Î(t,T ).
	î			max	t Î[0,t)
			ì-u
	4. u = í u max				t Î(t,T ).
	î			max
	Определим вид процесса в системе при двух возможных значениях сиг-
нала управления.
	Для				:
						x 2 (0) = C1 = x 20 ,	x 2 = umax t + x 20 ,
			x 2 = umax t + C1 ,
x 1	=	umax t 2		+ C1t + C2 ,		x 1(0) = C2 = x 10 ,	x 1 =	umax t 2	+ x 20t + x 10 .
	2						2

93

Исключим время из этих уравнений:

x

2

− x

20

u

max

æ x

2

- x

20

ö

2

x

2

- x

20

t =

, x 1 =

ç

÷

+ x 20

+ x10

,

umax

umax

umax

2 è

ø

1

æ x 2

x 2

2

ö

1

2

2

ç

2

20

÷

x 1 - x10

=

ç

- x 2x 20

+

+ x 2x 20 - x 20

÷

=

(x 2

- x 20 ).

2

2

2umax

umax è

ø

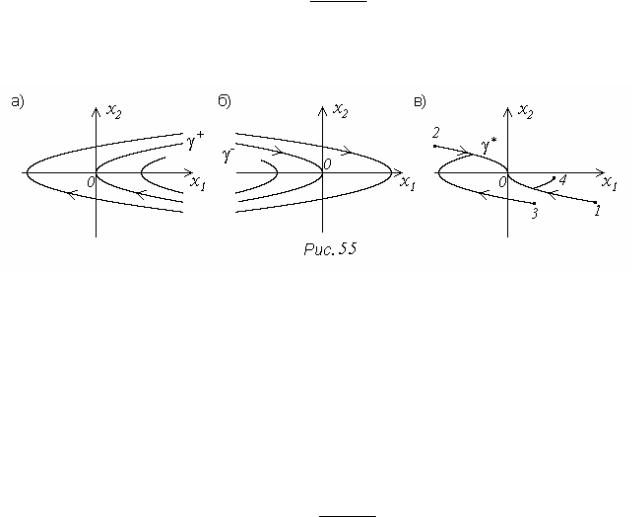
Соответствующие фазовые траектории (рис. 55а) будут представлять со- бой параболы, причем одна из них, уравнение которой

x 2

x 1 = 2u 2 ,

max

проходит через начало координат. Ее обозначим g+.

Для

:

u

t2

x

20

− x

2

x

2

= −u

t + x

20

,

x = - max

+ x

20

t + x

,

t =

,

max

1

2

10

umax

-1

æ x 2

x 2

2

ö

-1

2

2

ç

2

20

÷

x1 - x10

=

ç

- x 2 x 20 +

+ x 2 x 20

- x 20

÷

=

(x 2

- x 20 ).

2

2

2umax

umax è

ø

Соответствующие фазовые траектории (рис. 55б) будут иметь вид пара- бол, причем g− описывается уравнением

x 2 x1 = - 2u 2

max

и проходит через начало координат.

Таким образом, если точка (x10, x20), соответствующая начальным усло- виям, будет лежать на кривой g+ (рис. 55в), оптимальное по быстродействию управление будет иметь вид 1; если (x10, x20) окажется на кривой g− - вид 2; левее кривой γ , объединяющей g+ и g− - вид 3; правее кривой g - вид 4.

94

В первых двух случаях переключение отсутствует, в последних двух - имеет место одно переключение в момент времени, когда фазовая траектория

достигает кривой g . Следо-

вательно, кривая g является на фазовой плоскости (рис. 55) линией переключения для оптимального управле-

ния. Уравнение кривой g

дает условие переключения для оптимального управле- ния:

x1 = - x22u× x 2 .

max

Теперь можно записать уравнение оптимального по быстродействию за- кона управления следующим образом:

^

æ

x

×

x

ö

u(x

1

,x

2

) = u

signç

-x

1

-

2

2

÷ .

max

è

2umax

ø

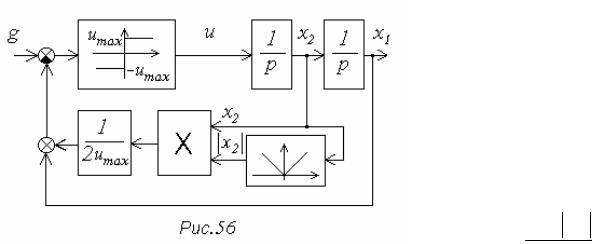
Структурная схема оптимальной по быстродействию системы стабилиза- ции показана на рис. 56.

95