u0 [n] = b0 x0 [n] + b1x0 [n − 1]+...+bl x0 [n − l] −
−a1u0 [n − 1] − a2 u0 [n − 2]−...−am u0 [n − m].	(13.5)

Как видно из (13.5), для формирования сигнала управления необходимо текущее значение сигнала ошибки, а также l его предыдущих значений и m предыдущих значений сигнала управления. Для их хранения используется опе- ративная память компьютера.

Лекция 14. Синтез системы управления. Обеспечение точности системы

Существуют два основных принципа синтеза систем управления:

-построение системы с обеспечением заданных требований к показателям

еекачества;

-построение системы, характеристики которой оптимальны в некотором смысле.

При использовании первого принципа, как правило, требуется обеспечить заданные точность и запас устойчивости системы.

Здесь рассмотрим наиболее простую и распространенную на практике методику, основанную на использовании частотных характеристик разомкну- той части системы.

Достоинством этой методики является единообразие синтеза непрерыв- ных и компьютерных систем, достигаемое благодаря анализу диапазонов час- тот, соответствующих ограничениям

ω ≤	2		или λ ≤ π				,		(14.1)
		T0		2			2T0
где ω - реальная частота сигнала,			λ =		tg	ωT0		- абсолютная псевдочастота,
						2
				T0

T0 - период дискретизации по времени в системе с компьютерным управлени- ем. Как отмечалось ранее, при выполнении указанных условий имеет место , и частотные характеристики непрерывной и компьютерной систем практически совпадают. Поэтому все положения методики синтеза и основные расчетные соотношения, разработанные для непрерывных систем, удается ис- пользовать без существенных изменений для компьютерных систем.

Если в компьютерной системе управления не удается обеспечить доста- точно малую для выполнения (14.1) величину периода дискретизации, преду-

сматривается возможность определения его допустимой величины или учет его реальной величины при расчете характеристик контура управления.

Наиболее простым, наглядным и широко используемым критерием точ- ности является максимальная ошибка системы при типовом входном сигнале.

54

Ошибкой, или сигналом ошибки, системы управления называется раз- ность x(t) = g(t) − y(t) или x[n] = g[n]− y[n] для решетчатых функций, где

g - задающее воздействие, y - выходной сигнал системы.

Наиболее общий случай, рассматриваемый при синтезе системы - гармо- нический входной сигнал g(t) = gmax sin(ω gt + ϕ g ). Выходной сигнал и сиг- нал ошибки в линеаризованной системе также будут гармоническими. Если из- вестна передаточная функция разомкнутой системы W(p) и главная обратная связь в системе единичная, амплитуда сигнала ошибки определяется следую- щим образом:

x max =

Фx (jω g )

gmax =

gmax

,

(14.2)

1

+W (jω g )

где Фx - передаточная функция замкнутой системы по ошибке. В реальных

системах обычно обеспечивается

W (jω g )

>> 1, и формула (14.2) может быть

заменена приближенной:

gmax

x max

≈

.

(14.3)

W (jω g )

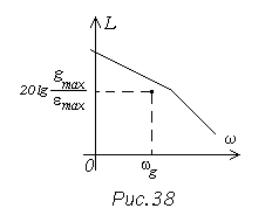
Формула (14.3) позволяет установить требования к низкочастотной части ЛАХ разомкнутой системы. Для того, чтобы максимальная ошибка замкнутой

системы при гармоническом воздействии не превышала заданного значения

εmax, ЛАХ разомкнутой системы должна проходить выше контрольной точки с координатами (рис. 38):

ω = ωg , L(ω g ) = 20 lg		W (jω g )		= 20 lg	gmax	.	(14.4)
					εmax

монический сигнал

.	..
gmax	= ωэ gэmax и gmax

Для входного сигнала произвольного вида, в том числе случайного, требования к ЛАХ синтезируемой системы могут быть по- лучены аналогичным способом, если извест-

ны максимально возможные значения первой

.

производной (скорости) gmax и второй про-

..

изводной (ускорения) gmax входного сигна-

ла. Для заданных значений этих характери- стик можно подобрать эквивалентный гар-

gэ (t) = gэmax sin(ωэt + ϕэ )

из

условий:

= ω2э gэmax . В результате можно получить:

55

		æ .		2		..
	1		ö			g	max
gэ max =		ç g	÷	,	wэ =			.	(14.5)
	..					.
		è	max ø
	gmax					gmax

Теперь при заданной максимальной допустимой ошибке emax в соответ- ствии с (14.4) могут быть получены координаты контрольной точки:

..

æ .

ö 2

ç g

÷

w = w

=

gmax

, L(w

) = 20 lg

W ( jw

)

= 20 lg

è

max ø

. (14.6)

э

.

э

э

..

gmax

emax gmax

.

Если для эквивалентного

гармонического

сигнала

предположить, что

..

.

gmax

= const , а gmax

® 0 , то при уменьшении gmax в 10 раз эквивалентная

частота уменьшится в 10 раз, а значение L(wэ) увеличится на 20 дБ, то есть контрольная точка будет смещаться влево по прямой с наклоном -20 дБ/дек. В

пределе получим режим работы системы при задающем воздействии вида

.

, и заданные значения gmax и emax будут определять тре-

буемое значение коэффициента передачи системы с астатизмом первого поряд- ка (добротность по скорости):

.

k = k v	=	gmax	.
		emax
Если для эквивалентного гармонического				сигнала предположить, что
..				.
gmax	= const , а			gmax	® 0 , то аналогично

можно показать, что контрольная точка будет смещаться вправо по прямой с наклоном - 40 дБ/дек.

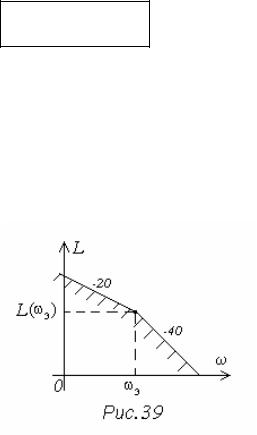
Область, расположенная ниже двух та- ких прямых должна рассматриваться как за- претная область для ЛАХ синтезируемой сис- темы (рис. 39). Это обеспечит заданную точ-

ность при известных максимальных значениях скорости и ускорения входного сигнала.

Полученной запретной области может соответствовать только астатическая система. Распространение полученных результатов на статические системы может быть выполнено, если принять ог- раничение не только на скорость и ускорение, но и на величину задающего воздействия gmax.

56

Подберем	эквивалентный		гармонический сигнал из условий:
	.	= ωэ gэmax .
gmax = gэ max ,	gmax		Тогда при заданной допустимой ошибке

εmax получим контрольную точку с координатами:

.

ω1	= ωэ =	gmax	,	L(ω1) = 20 lg	gmax	.			(14.7)
	.	gmax			εmax
Если уменьшать gmax при постоянной gmax ,					контрольная точка будес
сдвигаться влево по	горизонтальной			прямой на уровне 20 lg			gmax	,	а при
							εmax

.

уменьшении gmax при постоянной gmax - вправо по прямой с с наклоном -20

. ..

дБ/дек, пока будет выполняться условие ωэ gmax ≤ gmax . Далее следует вос-

..

пользоваться полученными выше результатами. После частоты ω2 = g. max

gmax

получим прямую с наклоном - 40 дБ/дек. Таким образом, при условии ограни-

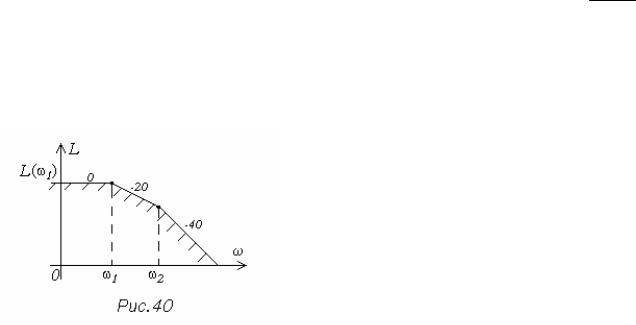
чения максимальной величины задающего воздействия запретная область для ЛАХ разомкнутой системы будет иметь вид, показанный на рис. 40.

Для системы компьютерного управ- ления полученные результаты также спра- ведливы, если вся запретная область оказы- вается в диапазоне частот, соответствую- щих (14.1). Запретная область для логариф-

мической псевдочастотной характеристики будет соответствовать рис. 39 или рис. 40,

если заменить частоту ω на абсолютную псевдочастоту λ.

Лекция 15. Синтез системы управления. Обеспечение запаса устойчивости системы

В качестве показателей запаса устойчивости используются: запас устой- чивости по амплитуде, запас устойчивости по фазе и показатель колебательно- сти системы. Их можно определить на основе частотных характеристик.

Запасы устойчивости по амплитуде и по фазе для замкнутой системы оп- ределяются на основе частотных характеристик разомкнутой цепи. Их получе- ние на основе логарифмических частотных характеристик показано на рис. 41.

57

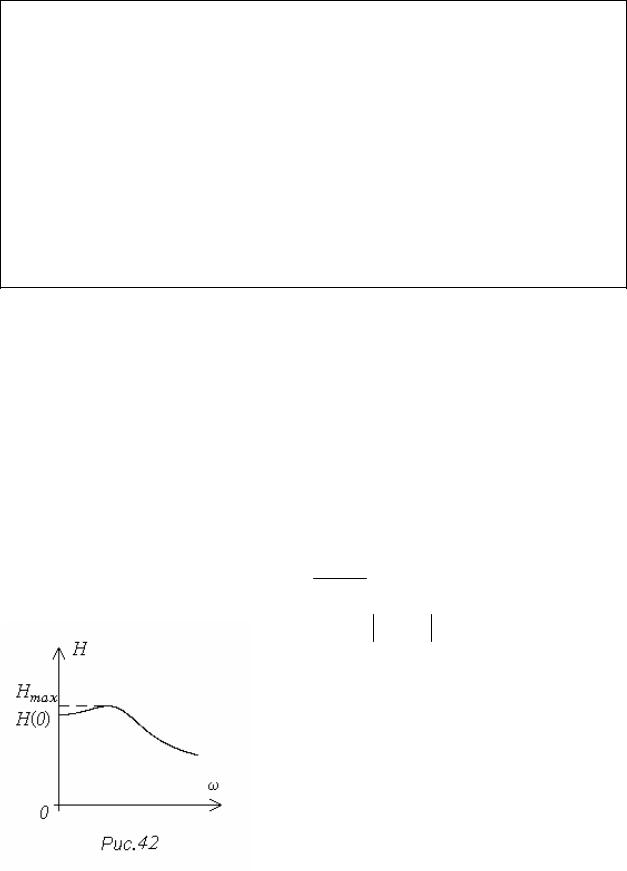
Запас устойчивости по амплитуде La определяется как расстояние до го-

ризонтальной оси от ЛАХ на частоте ω1, при которой ЛФЧХ пересекает эту ось, то есть ψ(ω1)= -180 о.

Запас устойчивости по фазе μψ определяется как расстояние до горизон- тальной оси от ЛФЧХ на частоте ω2, при которой ЛАХ пересекает эту ось, то есть L(ω2)=0:

μψ = 180o + ψ(ω2 ).

(15.1)

Показатель колебательности для замкнутой системы определяется по ее амплитудно-частотной характеристике (рис. 42) как отношение:

M = HHmax(0) .

где H (ω) = Ф( jω) - амплитудно-частотная

характеристика замкнутой системы, Ф(p) -

основная передаточная функция замкнутой системы. Более высокому запасу устойчивости

соответствует меньшее значение показателя колебательности.

В технических требованиях на систему чаще задается максимально допустимое зна- чение показателя колебательности. По нему на основе следующего приближенного соотно-

шения может быть определено допустимое значение запаса устойчивости по фазе:

	μψ ≤ arcsin	1	(15.2)
		M
			58

или построена запретная область для амплитудно-фазовой частотной характе- ристики (рис. 43а) или ЛФЧХ (рис. 43б) разомкнутой системы.

	На рис. 43а центр окружности				имеет горизонтальную координату
−	M 2		, радиус окружности R =	M		.
	M 2 − 1			M 2
					− 1

На рис. 43б границы запретной области вдоль оси частот определяются условием:

	20 lg	M		≤ L ≤ 20 lg	M		.
		M + 1			M − 1

Наиболее часто задаются следующие требования по запасу устойчивости системы:

-запас устойчивости по амплитуде не менее 10-30 дБ;

-запас устойчивости по фазе не менее 30-60о;

-показатель колебательности не более 1-1,7.

Для решения задач синтеза, то есть выбора закона управления или расче-

та корректирующего устройства наиболее удобный математический аппарат разработан применительно к логарифмическим частотным характеристикам.

При этом следует иметь в виду, что вид низкочастотной части характери-

стик выбирается с точки зрения обеспечения точностных показателей системы и должен остаться неизменным. Поэтому правила обеспечения запаса устойчи- вости разработаны для нескольких вариантов так называемых типовых ЛАХ.

Для систем с астатизмом второго порядка существенный для рассматри- ваемой задачи участок типовой ЛАХ показан на рис. 44. Ему соответствует пе-

редаточная функция

	W (p) =	k(1+ T1 p)		,	T1 > T2 .
		p2	(1+ T2 p)

59

Базовая частота связана с коэффици- ентом передачи соотношением: w0 = 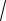k ,

а частота среза определяется через базовую частоту: wc = w02T1 = kT1.

Для обеспечения заданного значения показателя колебательности M длина уча- стка ЛАХ с наклоном -20 дБ/дек должна составлять не менее:

	h =	ω2	=		T1	=	M + 1		. (15.3)
		w1		T2			M - 1

Рекомендуемые значения постоянных времени определяются соотноше- ниями:

T1	=			1					M		,			(15.4)
			w0						M - 1
T2 =	1						M (M - 1)						.	(15.5)
		w0
							M + 1

Соотношения (15.4) - (15.5) иногда выражают через частоту среза и ис- пользуют в виде неравенств:

	T1	³	1		M		,	(15.6)
			wс M - 1
	T2	£	1		M		.	(15.7)
			wс M + 1

При неравенствах в (15.6) - (15.7) обеспечивается дополнительный запас устойчивости, и показатель колебательности имеет меньшее значение.

Если в системе присутствуют другие инерционные звенья с меньшими постоянными времени:

W (p) =	k(1+ T1 p)	,
	p2 (1+ T2 p)(1+ T3 p)...(1+ Tn p)

постоянная времени T1 должна удовлетворять соотношению (15.4), а остальные постоянные времени должны удовлетворять одному из неравенств:

n	1			M (M - 1)
åTi £									,	(15.8)
	w0			M + 1
i=2
n			1 M
åTi £								.		(15.9)
			wс M + 1
i=2

60