MMATAN01

где

A = {x R : −1 ≤ x ≤ 1}, B = R, f (A) = {y R : 0 ≤ y ≤ 1}.

Здесь множество значений f (A) принадлежит множеству B = R,

f (A) B

—это одна возможная ситуация.

2)Для функции y = x можем записать

x : R → R, A = R, B = R, f (A) = R.

В этом случае

f (A) = B

и мы наблюдаем другую ситуацию.

Различая два возможных случая в приведенных примерах, мы приходим к следующему определению.

	;y
;y	;;yy
Рис. 1.6. Отображения “ в ” и “ на ”

Определение 1.12. Пусть f : A → B.

1. Если f (A) B, то говорят, что f осуществляет отображение множества A “ в ” множество B.

2. Если f (A) = B, то говорят, что f осуществляет отображение множества A “ на ” множество B.

Заметим, что поскольку включение одного множества в другое не исключает равенства этих множеств (в приведенном только что определении включение f (A) B не исключает равенства

11

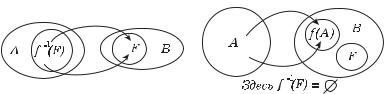
f (A) = B), то отображение множества A на множество B можно рассматривать одновременно как и отображение множества A в множество B (рис. 1.6).

Определение 1.13. Пусть задано отображение f : A → B и F B. П р о о б р а з о м множества F при этом отображении f : A → B называется множество элементов a A, для которых выполняется f (a) F .

Обозначение

f −1(F ) = {a A : f (a) F }.

Рис 1.7. Прообраз множества F

Определение 1.14. Пусть A и B — два множества. Отображение f : A → B называется в з а и м н о - о д н о з н а ч н ы м отображением A “в” B, если при каждом b B множество f −1(b) состоит не более чем из одного элемента множества A (либо один элемент, либо f −1(b) = ).

Определение 1.15. Если f : A → B есть взаимно-однозначное отображение A “на” B, то говорят, что f устанавливает взаимно-однозначное соответствие между множествами A и B. В этом случае говорят, что A и B э к в и в а л е н т н ы или имеют одинаковую м о щ н о с т ь , и пишут A B.

Определение 1.16. Пусть n N — любое натуральное число и In = {1, 2, 3, . . . , n}. Будем говорить, что:

12

1.Множество A — к о н е ч н о, если A In при некотором натуральном n (пустое множество также считается конечным).

2.Множество A — б е с к о н е ч н о, если A не является конечным.

1.3. Символика

I.Запись A B означает, что “утверждение A влечет за собой утверждение B”.

II. A B — “утверждения A и B эквивалентны”.

III. A B — “для выполнения A необходимо и достаточно выполнения B”.

IV. — символ отрицания. Например, A читается “не A”.

V.— квантор общности. Используется вместо слов “Для всех ...”, “Любой ...”.

VI. — квантор существования. Используется вместо слов “Существует ...”, “Имеется ...”.

VII. Символ “ , ” используется вместо слов “удовлетворяющих”. Используется также как и обычная запятая (разделительный знак).

VIII. Символ “ : ” используется вместо слов “Имеет место свойство ...”.

Предложения “Для всех ...” и “Существует ...” часто сопровождаются некоторыми ограничениями. Эти ограничения обычно записывают в круглых скобках.

П р и м е р ы

1) Определение четной функции f : R → R на языке символики записывается так

( x R) : f (−x) = f (x).

2) Нечетная функция f : (E R) → R

( x E) : f (−x) = −f (x).

13

3) Периодическая функция f : R → R

( T > 0)( x R) : f (x + T ) = f (x).

4) Возрастающая функция f : (E R) → R

( x1 E, x2 E, x1 < x2) : f (x1) < f (x2).

При построении отрицательных утверждений используют специальные правила, которые мы здесь приводим.

Правила построения отрицательных утверждений

1. При отрицании утверждений вида A B и A B

AB заменяется на A B,

AB заменяется на B A.

2.Отрицание свойства, содержащего некоторое число кванторов, , и свойства P (записанного после знака “ : ”) получается заменой каждого квантора на и на и свойства P на отрицание этого свойства P .

Пр и м е р.

Прямое утверждение

f : (E R) → R ограничена ( M > 0)( x E) : |f (x)| ≤ M.

Противоположное утверждение

f : (E R) → R неограничена ( M > 0)( x E) : |f (x)| > M.

1.4. Множество действительных чисел

Не вдаваясь в подробности, связанные с определением действительных чисел, займемся изучением их свойств (порой на интуитивном уровне). Прежде всего рассмотрим саму структуру множества действительных чисел, а затем введем важные понятия, необходимые при изучении как функций действительного переменного, так и других функций, в определении которых участвуют эти числа.

14

q — целые числа.

1.4.1. Структура множества действительных чисел

Рассмотрим числа в том порядке, как они исторически вводились по мере необходимости их применения.

1. Натуральные числа

Натуральные числа — это числа, которые появились в результате целочисленного счета

1, 2, 3, . . . n, . . .

Множество натуральных чисел обозначается буквой N.

2. Целые числа

Появились с введением отрицательных чисел (которые, по-види- мому, ввели должники). Это числа вида

0, ±1, ±2, . . .

Для множества целых чисел используют обозначение Z. Очевидно, что совокупность натуральных чисел — это часть совокупности целых чисел, т.е.

N Z.

3. Рациональные числа

Определение 1.17. Рациональным числом называется число, которое можно представить в виде несократимой дроби pq , где p и

Для множества рациональных чисел принято обозначение Q.

		2	=	1	,		3 =	−3
	П р и м е р ы:	4		2		−		1 .

Любое целое число k является рациональным, так как оно пред-

ставимо в виде	k	. Следовательно, справедливо следующее включе-
	1
ние		N Z Q.
		15

Определение 1.18. Два отрезка a и b называются соизмеримыми, если существует такой третий отрезок m, называемый их общей мерой, который целое число раз укладывается в отрезке a и в отрезке b. В противном случае отрезки a и b называются несоизмеримыми.

a

p раз

b

q раз m общая мера

Рис. 1.8. Соизмеримые отрезки

Пусть a и b — соизмеримые отрезки, а m — их общая мера, которая укладывается p раз в отрезке a и q раз в b. Примем отрезок b за единицу масштаба. Тогда если L[a] длина отрезка a, то L[b] = 1, L[m] = 1q и длина

p L[a] = p · L[m] = q

выражается рациональным числом.

Из приведенных рассуждений можно сделать следующий вывод. Рациональные числа служат для измерения физических величин, соизмеримых с выбранной единицей масштаба.

4.Иррациональные числа

Кпонятию иррационального числа нас приводит следующая, ставшая уже классической, теорема.

Теорема 1.1

Не существует рационального числа, квадрат которого равен 2.

16

Д о к а з а т е л ь с т в о. Предположим, что существует несократимая дробь pq , квадрат которой равен 2. Тогда

q		= 2 p2	= 2q2 p = 2m, m Z q2 = 2m2 q = 2k, k Z,
	p	2

т.е. дробь p сократима на 2. Полученное противоречие и доказывает теорему. q

√

Как следствие из этой теоремы можем заключить, что 2 не является рациональным числом. Такие числа называют иррациональными (приставка “ир” означает отрицание “не”).

B C

1

A D E

F

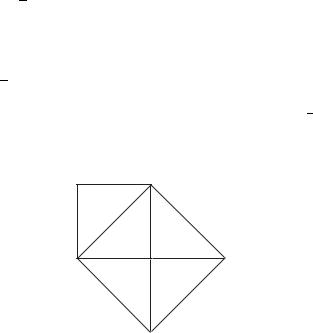
Рис. 1.9. Диагональ квадрата несоизмерима с его стороной

Выясним сущность иррационального числа. На рисунке 1.9 в качестве единицы масштаба выберем сторону квадрата L[AB] = 1. Обозначим длину диагонали квадрата через a, L[AC] = a. Тогда

a2 = SACEF = 4SADC = 2SABCD = 2,

т.е. длина диагонали AC квадрата ABCD измеряется иррациональным числом √2 и, следовательно, она несоизмерима с его стороной AB. Отсюда можно заключить, что иррациональные числа служат для измерения физических величин, несоизмеримых с выбранной единицей масштаба.

17

5. Действительные числа

Все рациональные и иррациональные числа принято называть действительными числами. С обозначением множества действительных чисел R мы уже встречались.

В множестве действительных чисел справедливы следующие включения

N Z Q R.

Множество иррациональных чисел является дополнением множества рациональных чисел до множества действительных чисел

R \ Q = CRQ.

Заметим, наконец, что множество рациональных чисел имеет собственные подмножества — это множества натуральных или целых чисел. Существует ли подобное собственное подмножество в множестве иррациональных чисел? Ответ на этот вопрос мы получим, если рассмотрим следующие понятия.

6. Алгебраические и трансцендентные числа

Определение 1.19. Действительное число называют алгебраическим, если оно является корнем некоторого уравнения n-й степени

a0xn + a1xn−1 + a2xn−2 + · · · + an−1x + an = 0

c целыми коэффициентами. В противном случае это число называется трансцендентным.

П р и м е р ы

1) Все рациональные числа — алгебраические. Действительно, каждое число вида pq , p Z, q Z, — корень уравнения

qx − p = 0

сцелыми коэффициентами.

2)Число π — трансцендентное число (этот факт мы примем без доказательства).

18

√

3) 2 — число алгебраическое, так как является корнем уравнения

x2 − 2 = 0.

Из этих примеров можно сделать вывод, что множество трансцендентных чисел — собственное подмножество множества иррациональных чисел.

На рисунке 1.10 схематически изображена структура множества действительных чисел.

Множество действительных чисел R

	Рациональные числа Q	Иррациональные числа R\Q
	Целые Z
	Натуральные N	Трансцендентные
		числа

Рис. 1.10. Структура множества действительных чисел

Как следствие следующей теоремы заключаем, что множество трансцендентных чисел бесконечное.

Теорема 1.2

Если b — трансцендентное число, то kb, где k Z, k = 0, — также трансцендентное число.

Д о к а з а т е л ь с т в о. Предположим, что kb — число алгебраическое, т.е. kb — корень уравнения

a0xn + a1xn−1 + · · · + an−1x + an = 0

с целыми коэффициентами. Тогда

a0(kb)n + a1(kb)n−1 + · · · + an−1(kb) + an ≡ 0

19

или

a0kn(b)n + a1kn−1(b)n−1 + · · · + an−1k(b) + an ≡ 0.

Откуда следует, что b — корень уравнения с целыми коэффициентами

a0knxn + a1kn−1xn−1 + · · · + an−1kx + an = 0,

т.е. b — алгебраическое число. Полученное противоречие и доказывает теорему.

1.4.2. Абсолютная величина действительного числа

Определение 1.20. Модулем или абсолютной величиной действительного числа называется само число, если оно неотрицательно, или противоположное ему число, если оно отрицательно. Математически это записывается так:

| |			a,	если a < 0.
a	=	a,		если a ≥ 0,
		−

Геометрически модуль (абсолютная величина действительного числа) a представляет расстояние d от точки, изображающей это число, до начала отсчета (рис. 1.11).

Рис. 1.11. Геометрический смысл модуля

Рассмотрим неравенство |x| ≤ a. Его решением является множество точек x, удаленных от начала на расстояние меньшее или равное a (рис. 1.12).

Таким образом, получаем формулу

|x| ≤ a −a ≤ x ≤ a.

(1.1)

20