
3Линейка / Задачник-1 / Глава 6
.DOCГлава 6
Квадратичные формы
§ 6.1. Билинейные формы. Приведение квадратичных форм к
каноническому виду методом Лагранжа
Билинейной
формой
в действительном линейном пространстве
![]() называется числовая функция
называется числовая функция
![]() удовлетворяющая следующим двум условиям:
удовлетворяющая следующим двум условиям:
![]()
![]()
Билинейная
форма
![]() называется симметричной,
если для любых векторов
называется симметричной,
если для любых векторов
![]() выполняется равенство
выполняется равенство
![]() .
.
![]()
Скалярное
произведение
![]() в евклидовом пространстве является
примером симметричной билинейной формы.
в евклидовом пространстве является
примером симметричной билинейной формы.
При
заданном базисе
![]() всякая билинейная форма в
всякая билинейная форма в
![]() мерном
действительном линейном пространстве
мерном
действительном линейном пространстве
![]() может быть записана в виде
может быть записана в виде
![]()
![]()
где
![]() -
координаты вектора
-
координаты вектора
![]() а
а
![]() -
координаты вектора
-
координаты вектора
![]() в данном базисе. Числа
в данном базисе. Числа
![]() зависят от выбора базиса и вычисляются
по формулам
зависят от выбора базиса и вычисляются
по формулам
![]()
![]()
![]()
Матрица
![]() называется матрицей
билинейной формы
называется матрицей
билинейной формы
![]() в базисе
в базисе
![]() .
.
Билинейная форма является симметричной тогда и только тогда, когда её матрица симметричная.
Пусть
![]() и
и![]() суть матрицы билинейной формы
суть матрицы билинейной формы
![]() в базисах
в базисах
![]() и
и
![]() соответственно. Тогда
соответственно. Тогда
![]()
![]()
где
![]() -
матрица
перехода
от базиса
-
матрица
перехода
от базиса
![]() к базису
к базису
![]() .
.
Для
того чтобы получить матрицу
![]() нужно разложить векторы
нужно разложить векторы
![]() по базису
по базису
![]() :
:
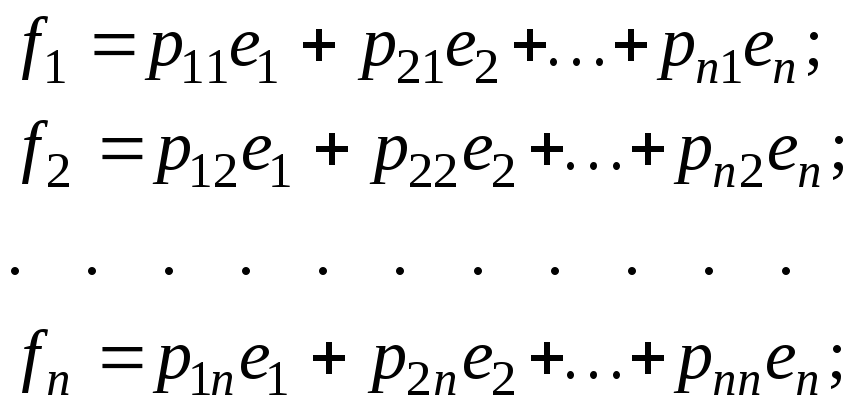
![]()
и составить из коэффициентов этих разложений таблицу:
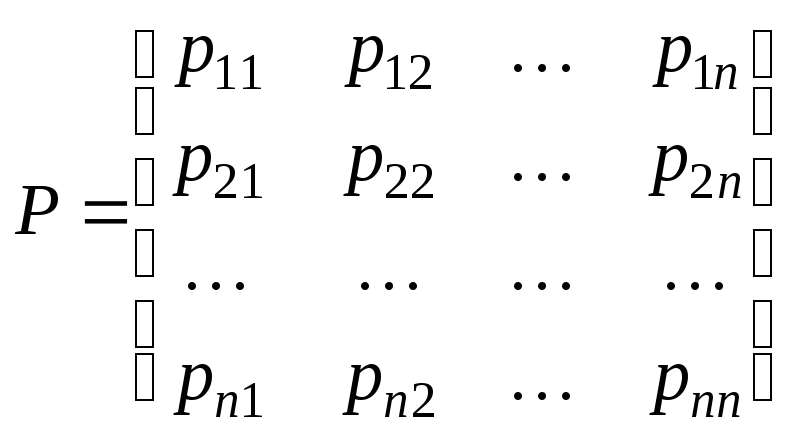 .
.
Пусть
![]() -
симметричная билинейная форма в линейном
пространстве
-
симметричная билинейная форма в линейном
пространстве
![]() .
Числовая функция
.
Числовая функция
![]() ,
которая получается из
,
которая получается из
![]() ,
если положить
,
если положить
![]() ,
называется квадратичной
формой.
,
называется квадратичной
формой.
При
заданном базисе
![]() всякая квадратичная форма в действительном
линейном пространстве
всякая квадратичная форма в действительном
линейном пространстве
![]() выражается формулой
выражается формулой
![]()
![]()
где
![]() -
координаты вектора
-
координаты вектора
![]() в данном базисе и
в данном базисе и
![]()
Пусть
в
![]() мерном
действительном линейном пространстве
мерном
действительном линейном пространстве
![]() задана произвольная квадратичная форма
задана произвольная квадратичная форма
![]() Тогда в
Тогда в
![]() существует базис
существует базис
![]() в котором эта квадратичная форма имеет
вид
в котором эта квадратичная форма имеет
вид
![]()
![]()
где
![]() -
координаты вектора
-
координаты вектора
![]() в базисе
в базисе
![]() При этом квадратичную форму
При этом квадратичную форму
![]() называют каноническим
видом квадратичной формы
называют каноническим
видом квадратичной формы
![]() Матрицей формы
Матрицей формы
![]() является диагональная матрица
является диагональная матрица
 .
.
Базис
пространства
![]() в котором квадратичная форма имеет
канонический вид, называют каноническим
базисом этой
квадратичной формы.
в котором квадратичная форма имеет
канонический вид, называют каноническим
базисом этой
квадратичной формы.
Пример
1.
Покажите, что отображение
![]()
![]() является симметричной билинейной формой
в пространстве
является симметричной билинейной формой
в пространстве
![]() Найдите матрицу билинейной формы
Найдите матрицу билинейной формы
![]() для случая
для случая
![]() в базисе
в базисе
![]()
Решение.
Покажем, что отображение
![]() является билинейной формой. Сумма
диагональных элементов квадратной
матрицы
является билинейной формой. Сумма
диагональных элементов квадратной
матрицы
![]() называется следом
матрицы
называется следом
матрицы
![]() и
обозначается
и
обозначается
![]() Известно, что
Известно, что
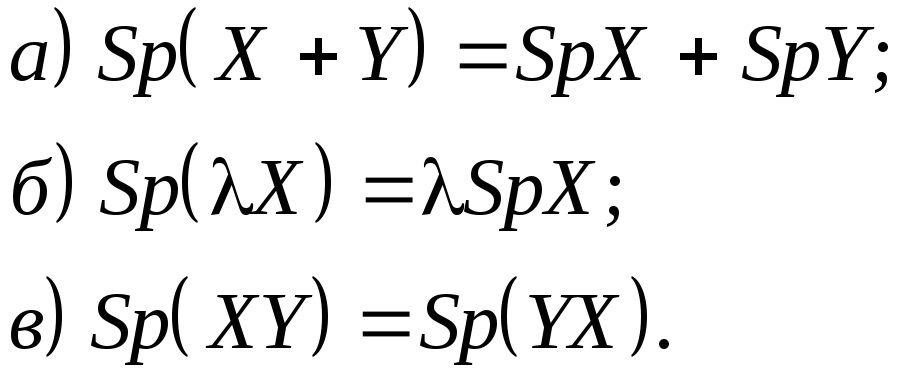
![]()
Поэтому
![]()
![]()
![]()
![]()
Следовательно,
по определению
![]() является билинейной формой.
является билинейной формой.
В силу того, что
![]()
отображение
![]() является симметричной билинейной
формой.
является симметричной билинейной
формой.
Построим
матрицу билинейной формы в базисе
![]() .
По формулам
.
По формулам
![]() находим:
находим:
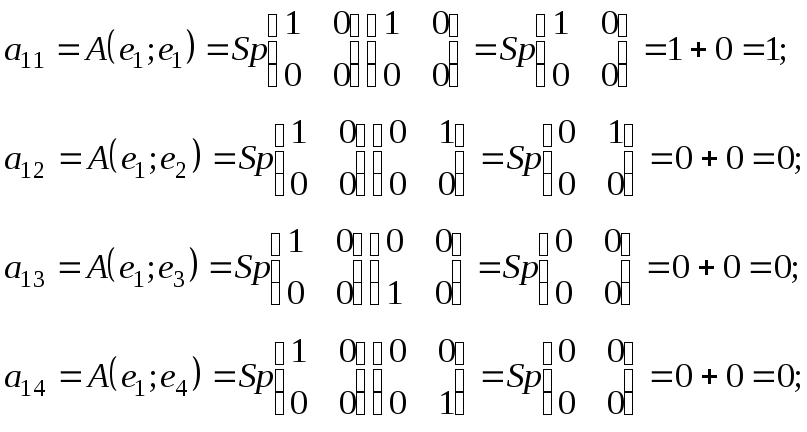
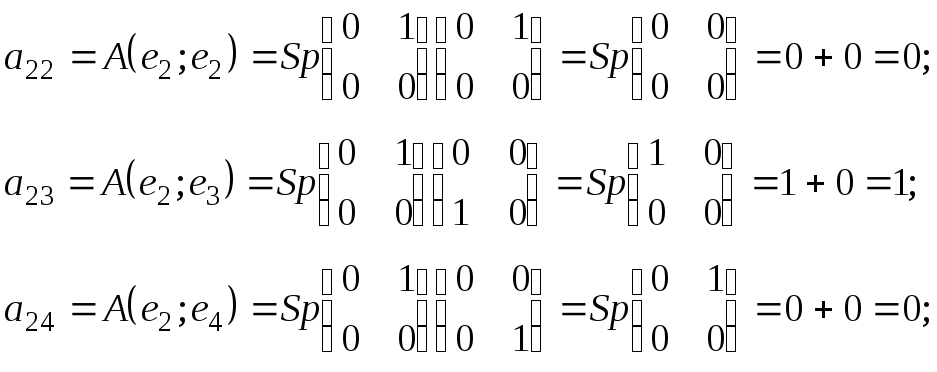
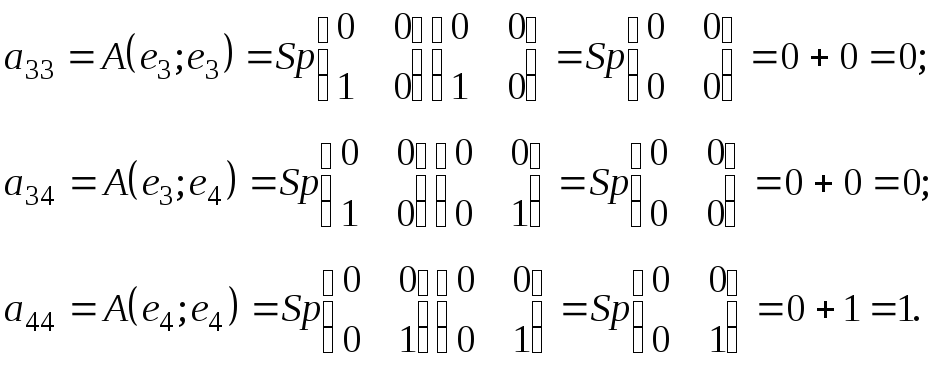
Учитывая,
что
![]() ,
окончательно получаем:
,
окончательно получаем:
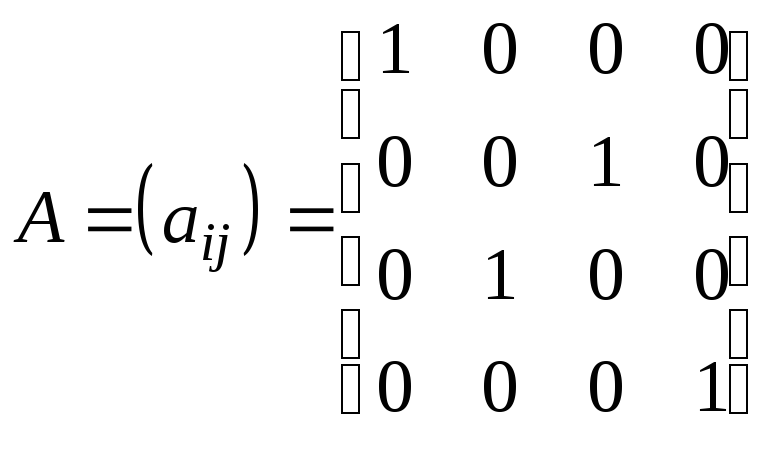 .
.
Пример
2.
Приведите методом
Лагранжа
к каноническому виду квадратичную форму
![]() и постройте канонический базис этой
квадратичной формы.
и постройте канонический базис этой
квадратичной формы.
Решение.
Основная идея метода Лагранжа заключается
в последовательном выделении в
квадратичной форме полных квадратов
по каждой переменной. Соберем в
квадратичной форме
![]() все члены, содержащие
все члены, содержащие
![]() ,
и дополним их сумму до полного квадрата:
,
и дополним их сумму до полного квадрата:
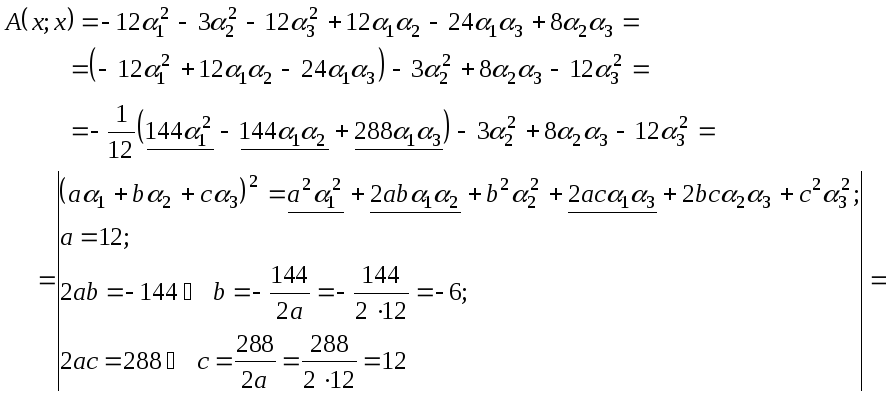
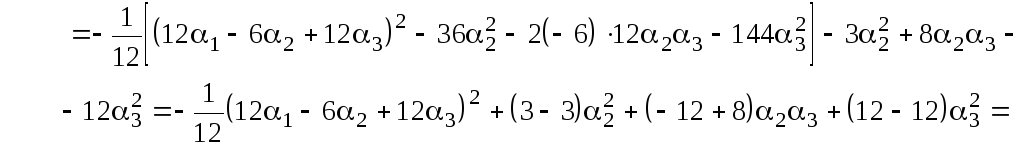
![]()
Далее
нужно в квадратичной форме от переменных
![]() группировать все слагаемые, содержащие
группировать все слагаемые, содержащие
![]() ,
и дополнять их сумму до полного квадрата.
Поскольку в нашем случае коэффициент
при
,
и дополнять их сумму до полного квадрата.
Поскольку в нашем случае коэффициент
при
![]() равен нулю, сделаем замену:
равен нулю, сделаем замену:
![]() .
.
В результате получим:
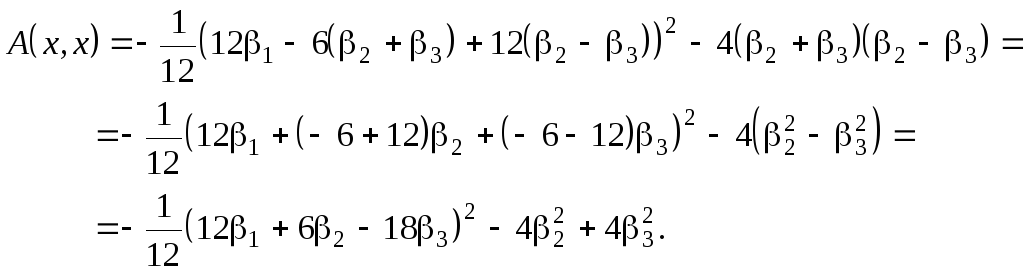
Положив в последнем выражении
![]() ,
,
записываем канонический вид квадратичной формы
![]()
и
переходим к построению канонического
базиса. Известно, что координаты вектора
![]() в старом и новом базисах связаны
посредством матрицы перехода соотношением
в старом и новом базисах связаны
посредством матрицы перехода соотношением
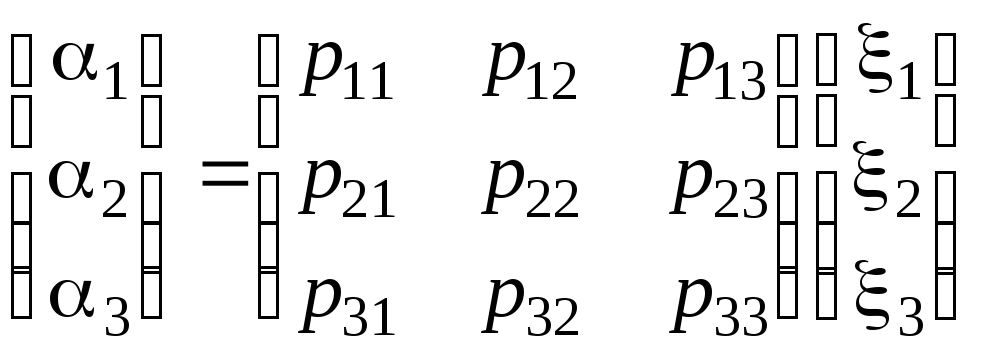 .
.
В нашем случае
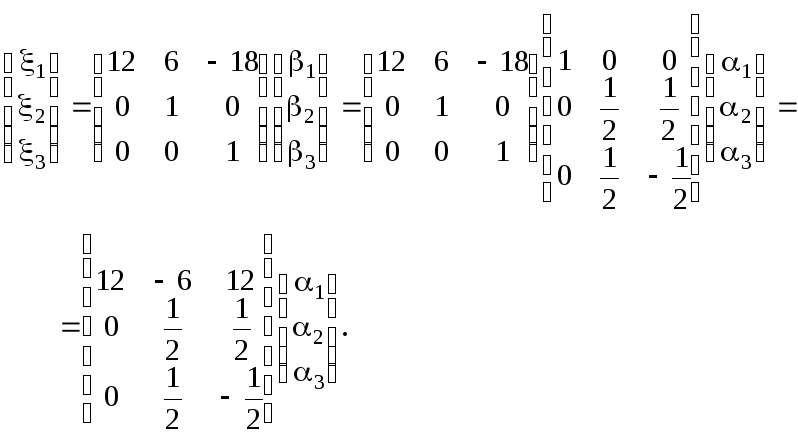
Отсюда
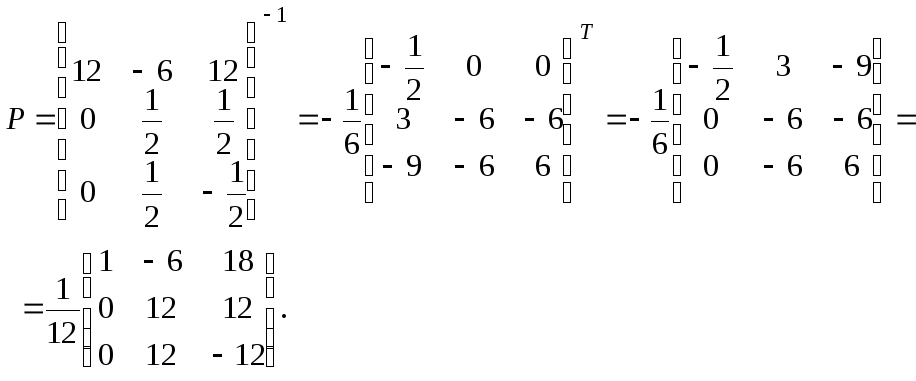
Столбцы
матрицы
![]() составляют канонический базис квадратичной
формы
составляют канонический базис квадратичной
формы
![]() .
.
Нетрудно
проверить, что
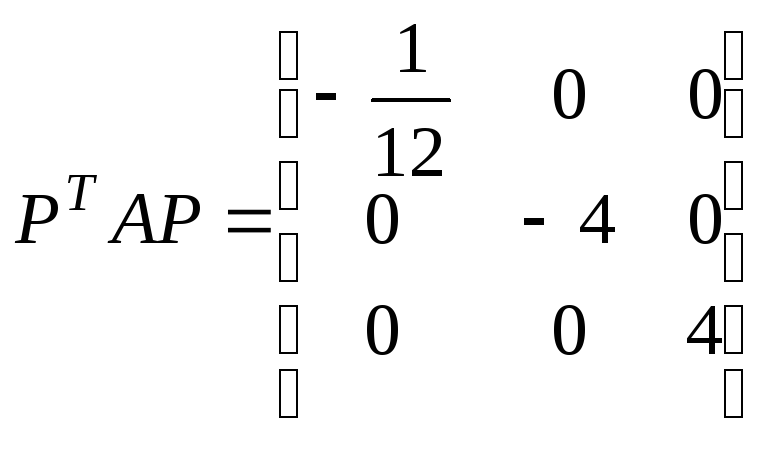 .
.
6.1.1.
Является ли билинейной формой в
![]() -
мерном действительном линейном
пространстве
-
мерном действительном линейном
пространстве
![]() функция
функция
![]() ,
где
,
где
![]() -
первые координаты векторов
-
первые координаты векторов
![]() и
и
![]() в некотором базисе?
в некотором базисе?
6.1.2.
Запишите матрицу билинейной формы
![]() в заданном базисе действительного
линейного пространства
в заданном базисе действительного
линейного пространства
![]() ,
если:
,
если:
![]()
![]() базис:
базис:
![]()
![]()
-
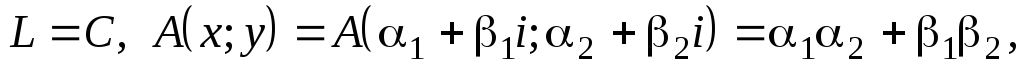 базис:
базис:
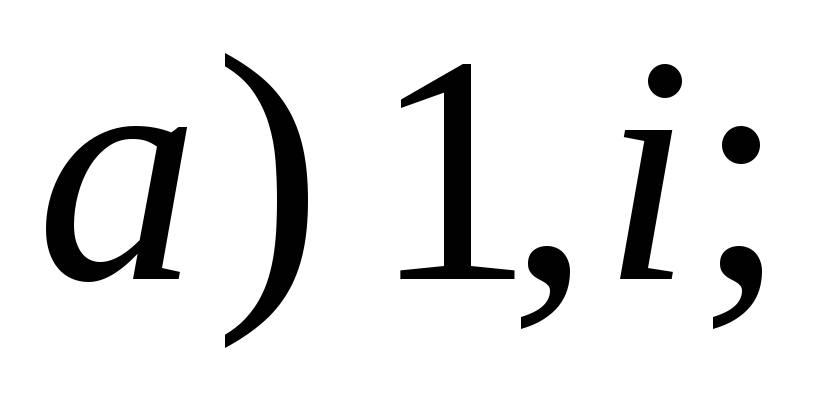
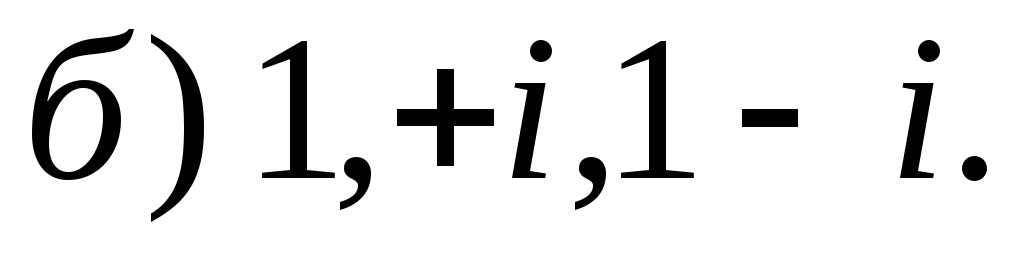
6.1.3.
Билинейная форма
![]() называется кососимметричной,
если для любых векторов
называется кососимметричной,
если для любых векторов
![]() выполняется равенство
выполняется равенство
![]() .
.
![]()
Убедитесь,
что отображение
![]() ,
определяемое равенством
,
определяемое равенством
![]() ,
,
является
кососимметричной билинейной формой в
пространстве
![]() .
.
Найдите
её матрицу в базисе
![]()
6.1.4. Запишите матрицу билинейной формы:
![]()
![]()
6.1.5. Найдите билинейную форму, если известна ее матрица
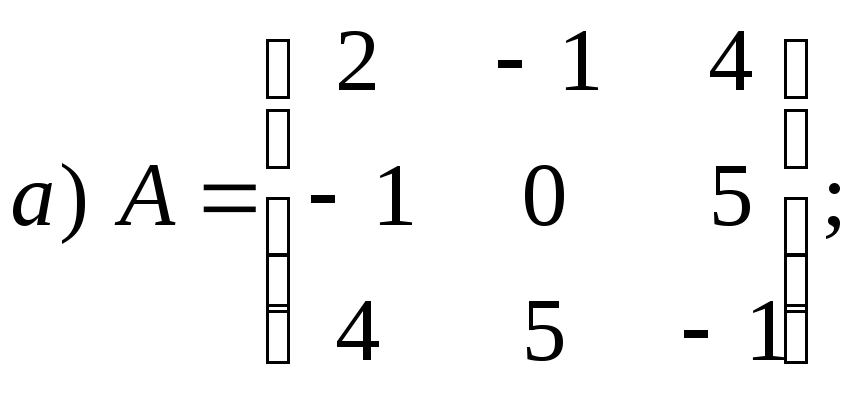
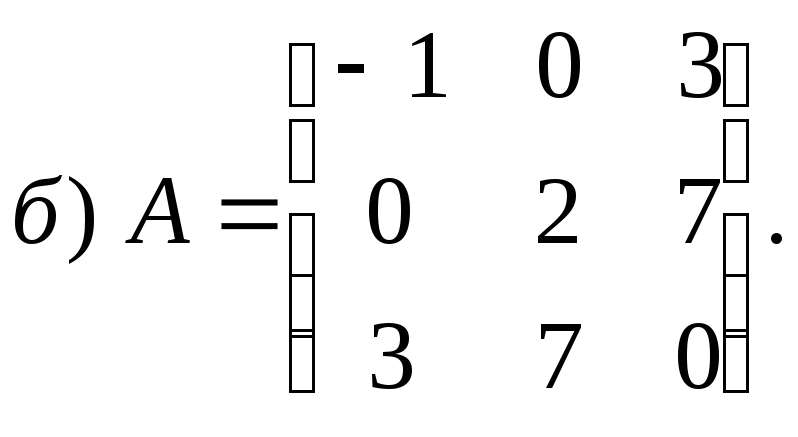
6.1.6. Методом Лагранжа приведите следующие квадратичные формы к каноническому виду и укажите невырожденное линейное преобразование переменных, приводящее к этому виду ( ввиду неоднозначности искомого линейного преобразования ответ может получиться отличным от приведенного):
![]()
![]()
![]()
![]()
![]()
![]()
![]()
§ 6.2. Приведение квадратичных форм к каноническому виду
методом Якоби. Знакоопределенные квадратичные формы
В
отличии от рассмотренного в предыдущем
параграфе метода Лагранжа, где канонический
базис
![]() квадратичной
формы
квадратичной
формы
![]() вычислялся за несколько шагов, в методе
Якоби векторы
вычислялся за несколько шагов, в методе
Якоби векторы
![]() ,
непосредственно выражаются через
исходный базис. Суть метода
Якоби
заключается в следующем.
,
непосредственно выражаются через
исходный базис. Суть метода
Якоби
заключается в следующем.
Пусть
в базисе
![]()
![]() мерного
действительного линейного пространства
мерного
действительного линейного пространства
![]() квадратичная форма имеет вид
квадратичная форма имеет вид
![]() ,
,
![]()
где
![]() ,
и определители
,
и определители
![]() ,
,
![]()

![]()
отличны от нуля. Тогда в базисе
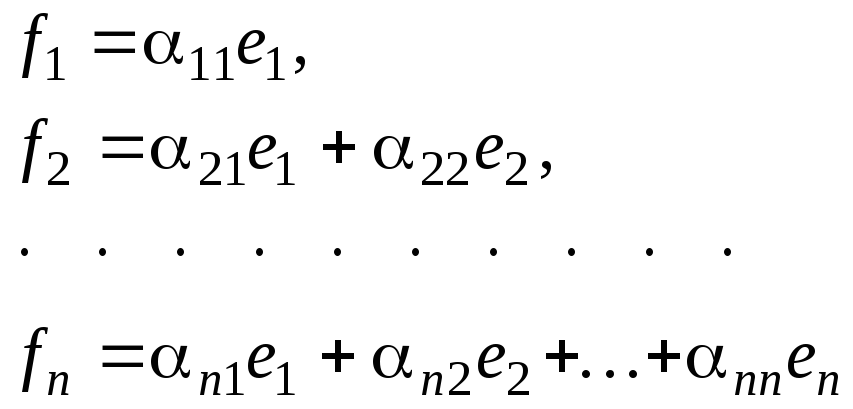
![]()
квадратичная
форма
![]() записывается в виде суммы квадратов :
записывается в виде суммы квадратов :
![]() ,
,
![]()
где
![]() -
координаты вектора
-
координаты вектора
![]() в базисе
в базисе
![]() .
.
Для
того чтобы найти коэффициенты
![]() в выражении
в выражении
![]() для
для
![]() ,
необходимо решить неоднородную систему
линейных уравнений вида
,
необходимо решить неоднородную систему
линейных уравнений вида
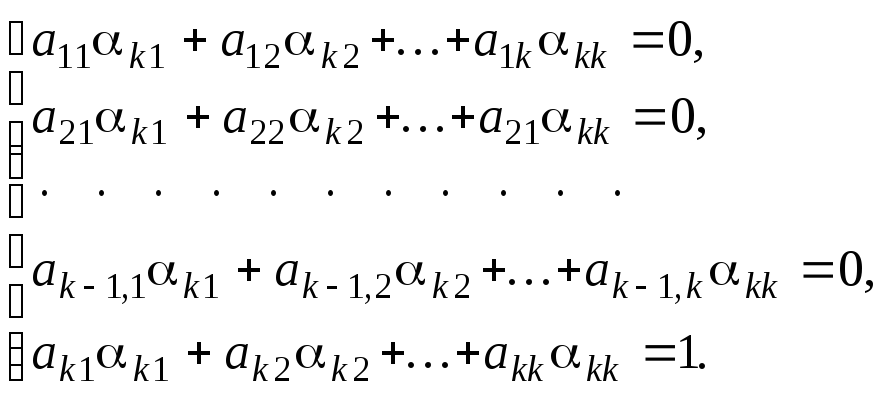
![]()
Известно, что задача нахождения канонического базиса квадратичной формы решается неоднозначно. Тем не менее можно утверждать, что число положительных, отрицательных и нулевых коэффициентов в любом каноническом представлении данной квадратичной формы всегда одно и то же (в этом состоит закон инерции квадратичных форм).
Квадратичную
форму
![]() называют положительно
(отрицательно)
определённой,
если для любого вектора
называют положительно
(отрицательно)
определённой,
если для любого вектора
![]() .
.
Скалярное произведение есть билинейная форма, соответствующая положительно определённой квадратичной форме , и любая такая форма может быть принята за скалярное произведение.
Справедлив
следующий признак положительной
определённости квадратичной формы
(критерий
Сильвестра)
: для того чтобы квадратичная форма
![]() была положительно определённой,
необходимо и достаточно, чтобы все
последовательные угловые миноры
была положительно определённой,
необходимо и достаточно, чтобы все
последовательные угловые миноры
![]() ,
определённые соотношением
,
определённые соотношением
![]() ,
были положительными.
,
были положительными.
Квадратичную форму, принимающую как положительные, так и отрицательные значения, называют знакопеременной.
Пример
1.
Методом Якоби приведите к каноническому
виду квадратичную форму
![]() и укажите канонический базис этой
квадратичной формы.
и укажите канонический базис этой
квадратичной формы.
Решение.
Запишем матрицу квадратичной формы
![]() и вычислим угловые миноры
и вычислим угловые миноры
![]() по формуле
по формуле
![]() :
:
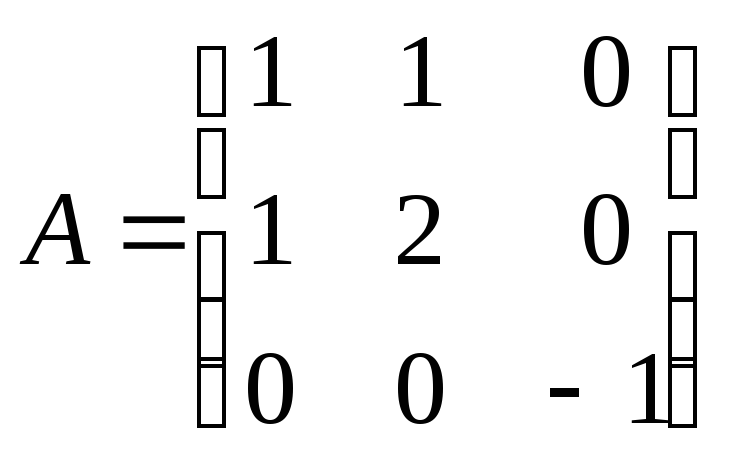 ;
;
![]()
![]()
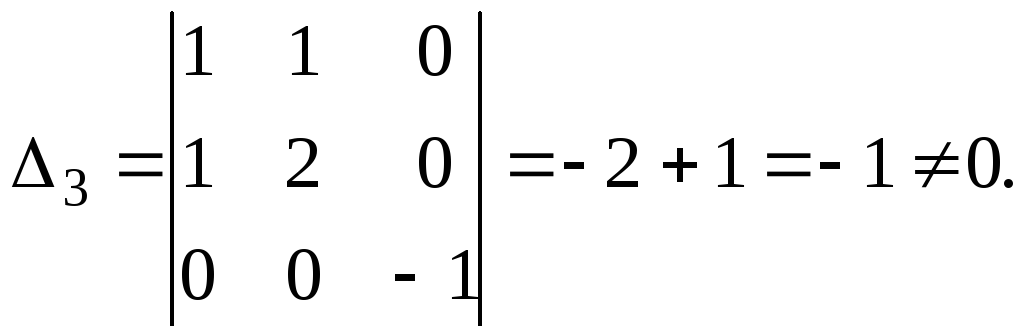
В
базисе
![]() ,
,
![]() ,
,
![]() квадратичная форма имеет канонический
вид:
квадратичная форма имеет канонический
вид:
![]()
Найдём
канонический базис
![]() последовательно применяя соотношение
последовательно применяя соотношение
![]() для
для
![]() :
:
![]() ;
;
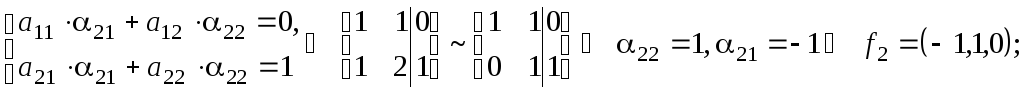
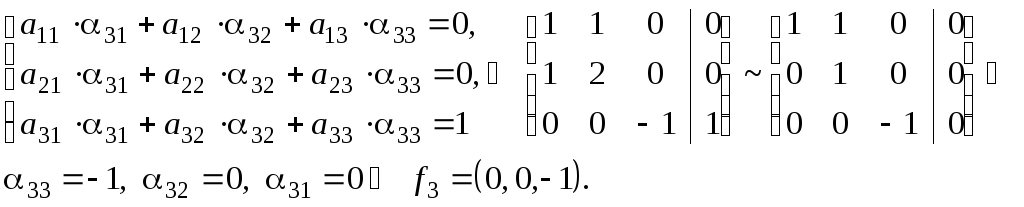
Составив
матрицу перехода
![]() от базиса
от базиса
![]() к базису
к базису
![]() ,
,
 ,
,
нетрудно
убедится в том, что
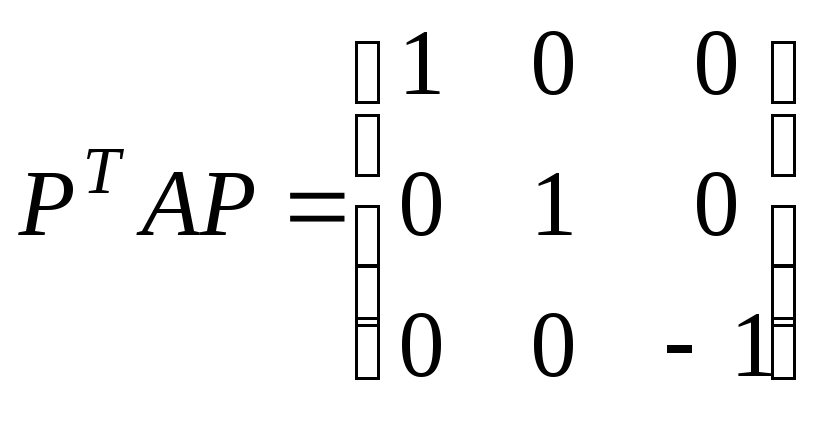 .
.
Пример
2.Найдите
все значения
![]() при которых положительно определена
квадратичная форма
при которых положительно определена
квадратичная форма
![]() .
.
Решение. Воспользуемся критерием Сильвестра. Запишем матрицу квадратичной формы

и
проверим, при каких
![]() все
угловые миноры этой матрицы будут
положительными:
все
угловые миноры этой матрицы будут
положительными:
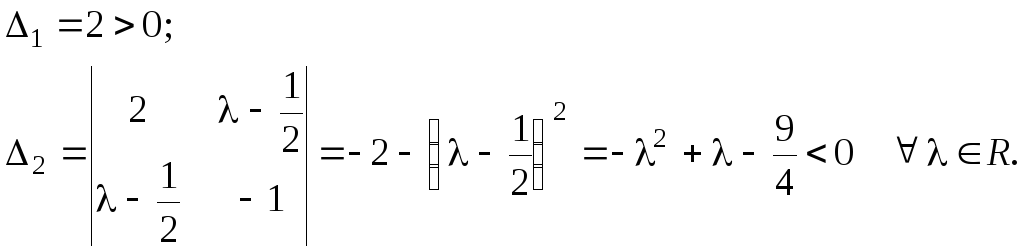
Следовательно,
не существуют значения
![]() ,
при которых данная квадратичная форма
положительно определена.
,
при которых данная квадратичная форма
положительно определена.
6.2.1. Методом Якоби приведите следующие квадратичные формы к каноническому виду и укажите канонические базисы квадратичных форм :
![]() ;
;
![]()
![]()
![]()
![]()
![]()
6.2.2.
Найдите все значения
![]() ,
при которых положительно определены
квадратичные формы:
,
при которых положительно определены
квадратичные формы:
![]()
![]()
![]()
![]()
6.2.3.
Докажите, что если квадратичная форма
с матрицей
![]() положительно определена, то и квадратичная
форма с матрицей
положительно определена, то и квадратичная
форма с матрицей
![]() положительно определена.
положительно определена.
6.2.4.
Докажите, что квадратичная форма
![]() отрицательно определена тогда и только
тогда, когда форма
отрицательно определена тогда и только
тогда, когда форма
![]() положительно определена.
положительно определена.
6.2.5.
Найдите все значения
![]() ,
при которых отрицательно определены
квадратичные формы:
,
при которых отрицательно определены
квадратичные формы:
![]()
![]()
![]()
