
3Линейка / Задачник-1 / Ответы и указания (1.2)
.DOC
![]() является
подпространством размерности
является
подпространством размерности
![]() ,
базис образуют, например, матрицы
,
базис образуют, например, матрицы
![]() ,
где
,
где
![]() -
матрица, элементы которой
-
матрица, элементы которой
![]() ,
а все остальные элементы- нули.
,
а все остальные элементы- нули.
3.5.2.
![]()
![]() -
пространство диагональных матриц;
-
пространство диагональных матриц;
![]()
![]() .
.
3.5.3
![]() Базис
Базис
![]() ,
например,
,
например,
![]() ,
базис
,
базис
![]() ,
например,
,
например,
![]() и
и
![]()
![]() базис
базис
![]() ,
например,
,
например,
![]() ,
базис
,
базис
![]() ,
например,
состоит
из векторов
,
например,
состоит
из векторов
![]() и
и
![]()
![]() базис
базис
![]() ,
например,
,
например,
![]() ,
базис
,
базис
![]() ,
например,
,
например,
![]() и
и
![]()
3.5.6.
![]()
3.5.8. Нет.
3.5.9.
![]() .
В качестве дополнительного подпространства
можно взять, например,
.
В качестве дополнительного подпространства
можно взять, например,
![]() и
и
![]()
4.1.1.
![]()
![]()
![]()
![]()
4.1.2. Ранг либо не изменится, либо изменится на единицу.
4.1.3.
Ранг изменится не более чем на единицу;
не более чем на
![]() .
.
4.1.5.
Нет. Контрпример:
![]()
4.1.7.
![]() 3;
3;
![]() 2;
2;
![]() 3.
3.
4.1.8.
![]()
![]() при
при
![]() ,
,
![]() при
при
![]() ;
;
![]()
![]() при
при
![]() ,
,
![]() при
при
![]() ,
,
![]() не может быть ни при каком
не может быть ни при каком
![]() ;
;
![]()
![]() при
при
![]() ,
,
![]() при
при
![]() .
.
4.1.9.
![]() Общее решение:
Общее решение:
![]() ;
фундаментальная система решений:
;
фундаментальная система решений:
![]() и
и
![]() ;
;
![]() общее
решение:
общее
решение:
![]() ;
фундаментальная система решений:
;
фундаментальная система решений:
![]() ,
,![]() ,
,![]() ;
;
![]() общее
решение:
общее
решение:
![]() ;
фундаментальная система решений:
;
фундаментальная система решений:
![]() ,
,
![]() ;
;
![]() общее
решение:
общее
решение:
![]() фундаментальная система решений:
фундаментальная система решений:
![]() ,
,
![]() .
.
4.1.10.
Строки матрицы
![]() не образуют, строки матрицы
не образуют, строки матрицы
![]() образуют.
образуют.
4.2.1.
![]()
![]()
![]()
![]()
![]() ;
;
![]() система
решений не имеет;
система
решений не имеет;
![]()
![]() ;
;
![]()
![]() .
.
4.2.2.
![]() При
При
![]() система несовместна
система несовместна
при
![]() система совместна и ее общее решение
таково:
система совместна и ее общее решение
таково:
![]() ;
;
![]() при
при
![]() система имеет единственное решение:
система имеет единственное решение:
![]() ,
при
,
при
![]() система несовместна;
система несовместна;
![]() система
совместна при любом значении
система
совместна при любом значении
![]() ,
при
,
при
![]() общее решение имеет вид:
общее решение имеет вид:
![]() ,
при
,
при
![]() общее решение таково:
общее решение таково:
![]() ;
;
![]() при
при
![]() система имеет единственное решение:
система имеет единственное решение:
![]() ,
при
,
при
![]() система несовместна,
при
система несовместна,
при
![]() система совместна, и ее общее решение:
система совместна, и ее общее решение:
![]() ;
;
![]() при
при
![]() система имеет единственное решение:
система имеет единственное решение:
![]() ,
,
при
![]() общее решение:
общее решение:
![]() ,
при
,
при
![]() система
несовместна.
система
несовместна.
4.2.3.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
5.1.2.
Указание:
пусть
![]() -
базис данного линейного пространства.
Для произвольных векторов
-
базис данного линейного пространства.
Для произвольных векторов
![]() и
и
![]() положим
положим
![]() .
Проверьте, что все аксиомы скалярного
произведения выполняются.
.
Проверьте, что все аксиомы скалярного
произведения выполняются.
5.1.6.
![]() Определяет;
Определяет;
![]() определяет, если
определяет, если
![]()
![]() не
определяет;
не
определяет;
![]() определяет.
определяет.
5.1.7.
Указание:
необходимость условия
![]() получите, рассматривая скалярный квадрат
получите, рассматривая скалярный квадрат
![]() вектора вида
вектора вида
![]() как квадратный трехчлен от
как квадратный трехчлен от
![]() .
.
5.1.8.
Да, если
![]() ;
нет, при
;
нет, при
![]() .
.
5.1.10.
![]() .
.
5.2.1.
![]() Не изменится;
Не изменится;
![]() заменится
на дополнительный (до
заменится
на дополнительный (до
![]() );
);
![]() не
изменится.
не
изменится.
5.2.2.
![]() .
Таким образом, треугольник равнобедренный.
Угол между
.
Таким образом, треугольник равнобедренный.
Угол между
![]() и
и
![]() равен
равен
![]() ,
так что треугольник прямоугольный. Угол
между
,
так что треугольник прямоугольный. Угол
между
![]() и
и
![]() равен
равен
![]() и является внутренним углом треугольника.
Угол между
и является внутренним углом треугольника.
Угол между
![]() и
и
![]() равен
равен
![]() ,
поэтому внутренним углом треугольника
является угол между
,
поэтому внутренним углом треугольника
является угол между
![]() и
и
![]() .
.
5.2.10.
![]()
![]()
![]()
![]() .
.
5.2.11.
Если
![]() ,
то
,
то
![]() .
.
![]()
![]()
![]()
![]() .
.
5.2.13.
![]() Например, можно добавить векторы
Например, можно добавить векторы
![]()
![]()
![]()
![]()
![]()
![]()
![]()
5.2.14.
![]() Например, вектором
Например, вектором
![]()
![]()
![]()
![]() например,
например,
![]()
5.2.15.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
5.3.2.
Например,
![]()
5.3.3.
Например,
![]()
5.3.4. Одномерное подпространство многочленов, все коэффициенты которых равны.
5.3.5.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
5.4.2. Указание:
Как и в задаче 5.1.2., фиксируем базис
![]() и для произвольных векторов
и для произвольных векторов
![]() и
и
![]() полагаем
полагаем
![]()
5.4.8.
![]() .
.
6.1.1. Нет.
6.1.2.
![]()
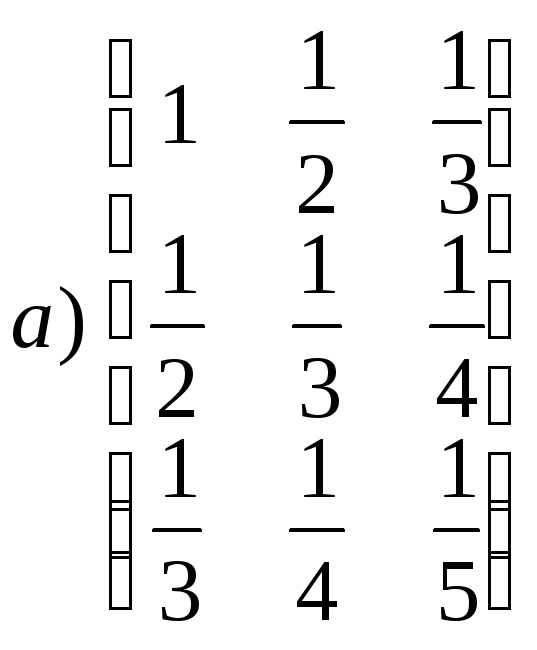 ;
;
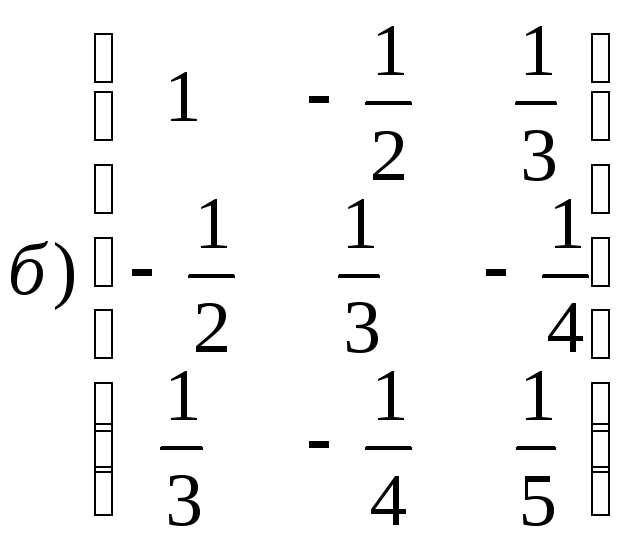 ;
2)
;
2)
![]() ;
;
![]() .
.
6.1.3.
![]()
6.1.4.
![]()
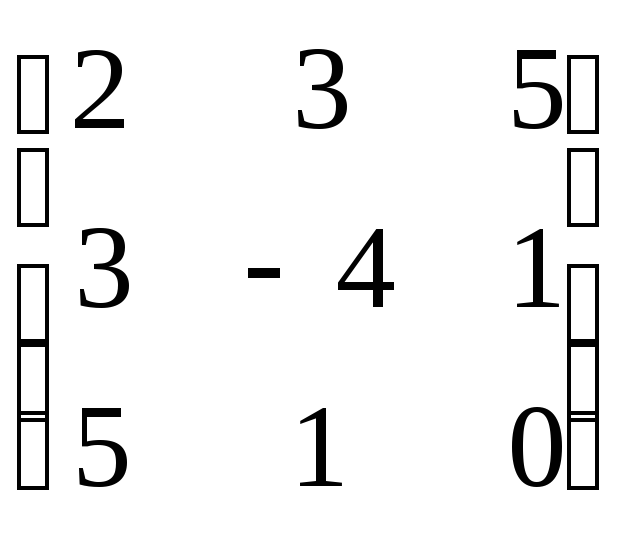 ;
;
![]()

6.1.5.
![]()
![]()
![]()
![]()
6.1.6.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
6.2.1.
![]()
![]() ;
;
![]() ;
;
![]()
![]() ;
;
![]() ;
;
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() .
.
6.2.2.
![]()
![]() ;
;
![]()
![]() ;
;
![]() таких
таких
![]() не существует;
не существует;
![]()
![]() .
.
6.2.5.
![]() Таких
Таких
![]() не существует;
не существует;
![]()
![]() ;
;
![]()
![]() .
.
