
3Линейка / Задачник-3 / Глава 8(1)
.docГЛАВА 8
ЭЛЕМЕНТЫ АНАЛИТИЧЕКОЙ ГЕОМЕТРИИ
§ 8.1. ПРЯМЫЕ В АФФИННОМ ПРОСТРАНСТВЕ
Пусть
дано множество
![]() элементов
элементов
![]() ,
называемых точками, и линейное пространство
,
называемых точками, и линейное пространство
![]() над полем
над полем
![]() с элементами
с элементами
![]() ,
называемыми векторами. Пусть, далее,
каждой упорядоченной паре точек
,
называемыми векторами. Пусть, далее,
каждой упорядоченной паре точек
![]() и
и
![]() из
из
![]() поставлен в соответствие единственный
вектор
поставлен в соответствие единственный
вектор
![]() из линейного пространства
из линейного пространства
![]() причем для этого соответствия выполняются
следующие две аксиомы:
причем для этого соответствия выполняются
следующие две аксиомы:
![]() для
любой точки
для
любой точки
![]() из
из
![]() и любого вектора
и любого вектора
![]() из
из
![]() существует в
существует в
![]() единственная точка
единственная точка
![]() такая, что
такая, что
![]() ;
;
![]() для
любых точек
для
любых точек
![]() из
из
![]() выполняется “правило треугольника”
выполняется “правило треугольника”
![]() .
.
Множество
![]() вместе с таким соответствием называется
аффинным
пространством,
связанным с линейным пространством
вместе с таким соответствием называется
аффинным
пространством,
связанным с линейным пространством
![]() Если линейное пространство
Если линейное пространство
![]()
![]() - мерное, то и аффинное пространство
- мерное, то и аффинное пространство
![]() называется
называется
![]() - мерным аффинным пространством и
обозначается через
- мерным аффинным пространством и
обозначается через
![]() .
.
Системой
координат
или репером
в аффинном пространстве
![]() называется упорядоченный набор
называется упорядоченный набор
![]() ,
(8.1.1)
,
(8.1.1)
состоящий
из некоторой точки
![]() из
из
![]() ,
называемой началом
координат,
и некоторого базиса
,
называемой началом
координат,
и некоторого базиса
![]() линейного пространства
линейного пространства
![]() Система координат называется прямоугольной,
если базис
Система координат называется прямоугольной,
если базис
![]() ортонормированный.
ортонормированный.
Координатами
точки
![]() в
системе координат
(8.1.1) называются координаты
в
системе координат
(8.1.1) называются координаты
![]() ее радиус - вектора
ее радиус - вектора
![]() в базисе
в базисе
![]() ,
т.е. коэффициенты из разложения
,
т.е. коэффициенты из разложения
![]() .
.
Точку
![]() с
координатами
с
координатами
![]() будем
обозначать
через
будем
обозначать
через
![]() ,
а вектор
,
а вектор
![]() с координатами
с координатами
![]() - соответственно через
- соответственно через
![]() .
.
Если
в аффинном пространстве
![]() даны координатами в системе (8.1.1)
две точки
даны координатами в системе (8.1.1)
две точки
![]() и
и
![]() ,
то
,
то
![]() ,
т.е. координаты вектора
,
т.е. координаты вектора
![]() равны разностям соответствующих
координат конца и начала вектора.
равны разностям соответствующих
координат конца и начала вектора.
Пусть
в аффинном пространстве
![]() зафиксирована система координат (8.1.1),
заданы точка
зафиксирована система координат (8.1.1),
заданы точка
![]() и направляющий вектор
и направляющий вектор
![]() .
Тогда множество точек аффинного
пространства
.
Тогда множество точек аффинного
пространства
![]() ,
радиус - векторы
,
радиус - векторы
![]() которых удовлетворяет уравнению
которых удовлетворяет уравнению
![]() ,
(8.1.2)
,
(8.1.2)
где
![]() и параметр
и параметр
![]() принимает любые значения из поля
принимает любые значения из поля
![]() называется прямой
проходящей через точку
называется прямой
проходящей через точку
![]() параллельно вектору
параллельно вектору
![]() .
Соотношение (8.1.2) называется параметрическим
уравнением прямой в векторной форме.
.
Соотношение (8.1.2) называется параметрическим
уравнением прямой в векторной форме.
Векторное
уравнение (8.1.2) равносильно
![]() координатным уравнениям
координатным уравнениям
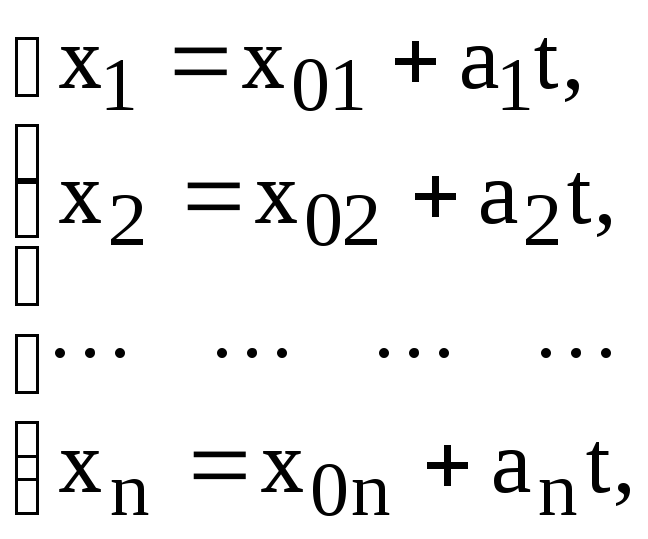 (8.1.3)
(8.1.3)
которые называются параметрическими уравнениями прямой в координатной форме.
Исключая
параметр
![]() в уравнениях (8.1.3), получаем каноническое
уравнение прямой
в аффинном пространстве
в уравнениях (8.1.3), получаем каноническое
уравнение прямой
в аффинном пространстве
![]()
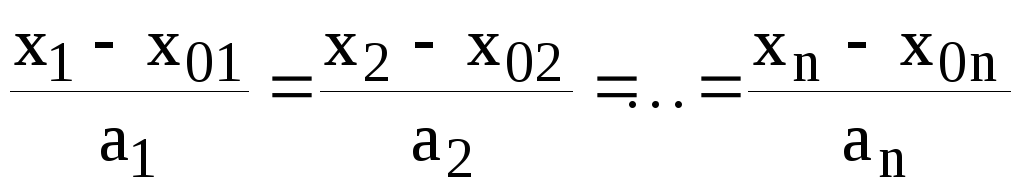 .
(8.1.4)
.
(8.1.4)
Если
на прямой известны две различные точки
![]() и
и
![]() ,
то уравнение этой прямой в векторной
форме
,
то уравнение этой прямой в векторной
форме
![]() (8.1.5)
(8.1.5)
и в канонической форме
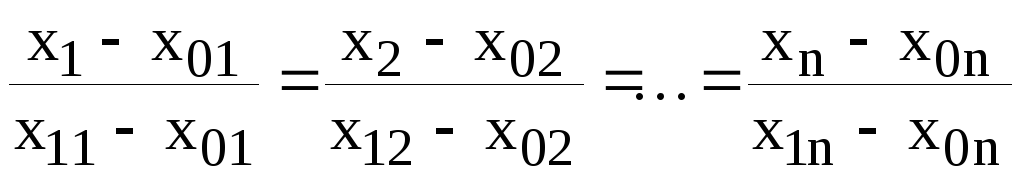 .
(8.1.6)
.
(8.1.6)
Угол
![]() между двумя прямыми
с направляющими векторами
между двумя прямыми
с направляющими векторами
![]() и
и
![]() определяется как угол между векторами
определяется как угол между векторами
![]() ,
не превышающий
,
не превышающий
![]() ,
и вычисляется по формуле
,
и вычисляется по формуле
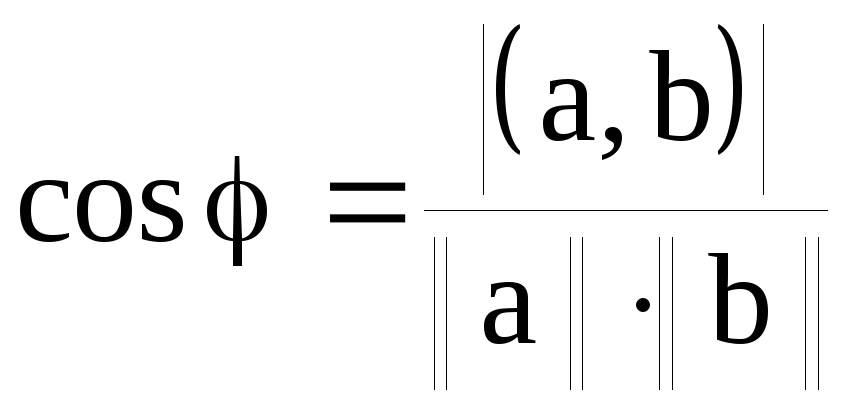 .
(8.1.7)
.
(8.1.7)
Необходимым
и достаточным условием того, чтобы две
прямые в аффинном пространстве
![]() ,
заданные векторными уравнениями
,
заданные векторными уравнениями
![]() и
и
![]() ,
пересекались или были параллельны,
является линейная зависимость тройки
векторов
,
пересекались или были параллельны,
является линейная зависимость тройки
векторов
![]() .
В случае скрещивающихся прямых векторы
.
В случае скрещивающихся прямых векторы
![]() линейно независимы. Направляющие векторы
параллельных прямых коллинеарны, т.е.
линейно независимы. Направляющие векторы
параллельных прямых коллинеарны, т.е.
![]() .
.
Расстояние
![]() от точки
от точки
![]() с радиусом - вектором
с радиусом - вектором
![]() до
прямой,
заданной уравнением (8.1.2), определяется
как минимальное расстояние от точки
до
прямой,
заданной уравнением (8.1.2), определяется
как минимальное расстояние от точки
![]() до точек прямой и вычисляется по формуле
до точек прямой и вычисляется по формуле
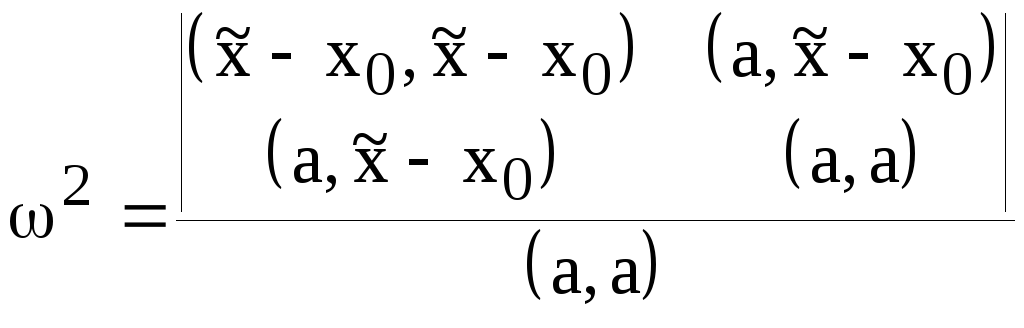 .
(8.1.8)
.
(8.1.8)
Основание
![]() перпендикуляра, опущенного из данной
точки
перпендикуляра, опущенного из данной
точки
![]() на прямую, совпадает с той точкой прямой,
которая находится на минимальном
расстоянии от данной точки.
на прямую, совпадает с той точкой прямой,
которая находится на минимальном
расстоянии от данной точки.
Расстояние
![]() между двумя скрещивающимися прямыми
с уравнениями
между двумя скрещивающимися прямыми
с уравнениями
![]() и
и
![]() определяется как кратчайшее расстояние
между точками этих прямых и вычисляется
по формуле
определяется как кратчайшее расстояние
между точками этих прямых и вычисляется
по формуле
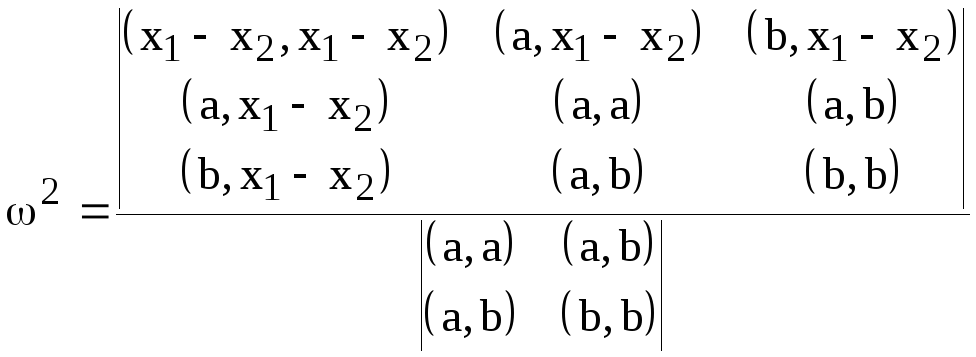 .
(8.1.9)
.
(8.1.9)
Основания общего перпендикуляра двух прямых совпадают с теми точками этих прямых, расстояние между которыми минимально.
Пример
1.
Найдите условия, необходимые и достаточные
для того, чтобы через точку, заданную
вектором
![]() ,
можно было провести единственную прямую,
пересекающую две прямые
,
можно было провести единственную прямую,
пересекающую две прямые
![]() и
и
![]() .
Укажите метод построения такой прямой
и точек пересечения ее с данными прямыми.
.
Укажите метод построения такой прямой
и точек пересечения ее с данными прямыми.
Решение.
Пусть
![]() - уравнение искомой прямой. Тогда
необходимые и достаточные условия для
того, чтобы прямая
- уравнение искомой прямой. Тогда
необходимые и достаточные условия для
того, чтобы прямая
![]() пересекала
прямые
пересекала
прямые
![]() и
и
![]() состоят в том, что системы векторов
состоят в том, что системы векторов
![]() и
и
![]() линейно независимы, вектор
линейно независимы, вектор
![]() линейно выражается через
линейно выражается через
![]() и вектор
и вектор
![]() линейно выражается через
линейно выражается через
![]() .
Формально это означает, что существуют
действительные значения
.
Формально это означает, что существуют
действительные значения
![]() такие, что
такие, что
![]() (8.1.10)
(8.1.10)
![]() ,
(8.1.11)
,
(8.1.11)
причем
![]() и
и
![]() .
Выразив
.
Выразив
![]() из соотношений (8.1.10), (8.1.11), получим
соответственно формулы
из соотношений (8.1.10), (8.1.11), получим
соответственно формулы
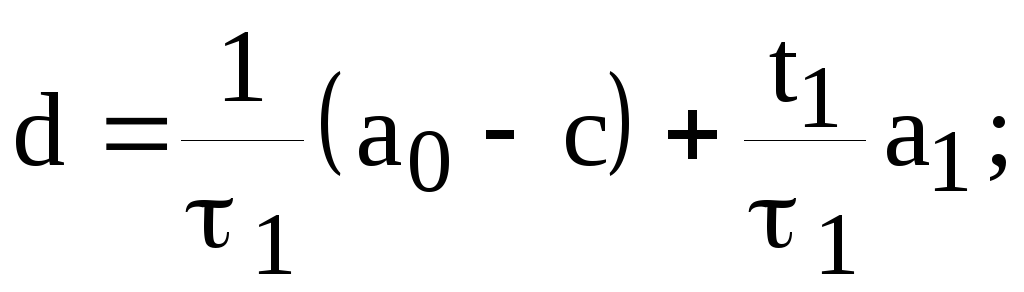 (8.1.12)
(8.1.12)
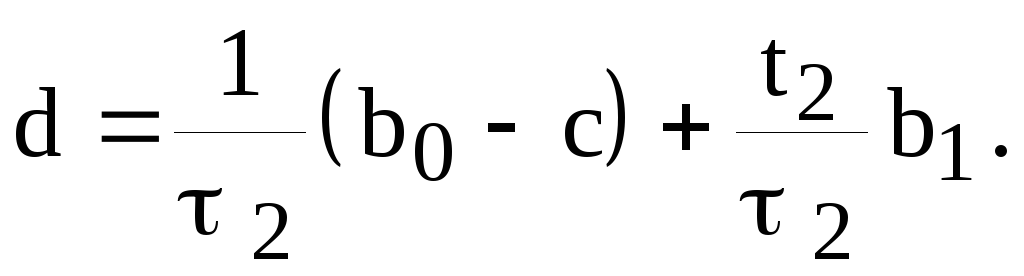 (8.1.13)
(8.1.13)
Вычитая
равенство (8.1.13) из (8.1.12), приходим к
нулевой линейной комбинации системы
векторов
![]()
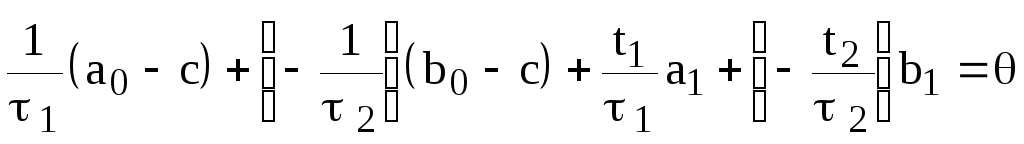 ,
,
в
которой коэффициенты
![]() и
и
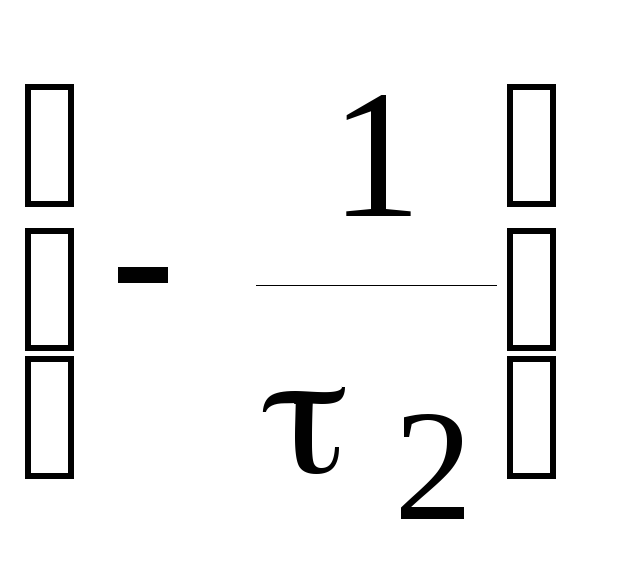 отличны от нуля, что говорит о линейной
зависимости указанной четверки векторов.
отличны от нуля, что говорит о линейной
зависимости указанной четверки векторов.
Подставив формулу (8.1.13) в (8.1.10), а формулу (8.1.12) в (8.1.11), получим две системы линейных алгебраических уравнений
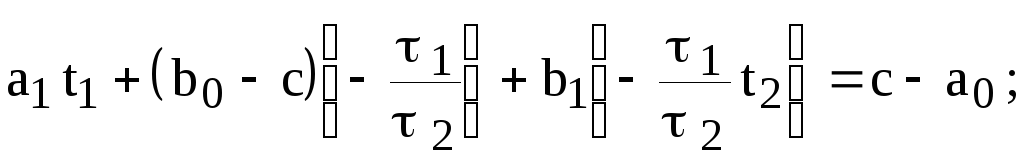 (8.1.14)
(8.1.14)
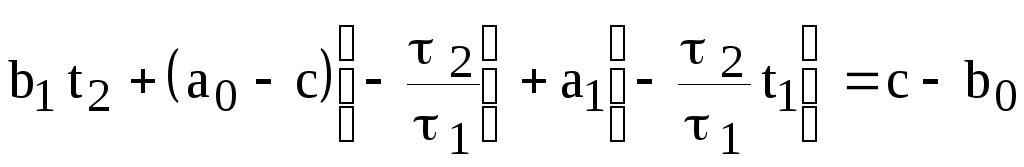 (8.1.15)
(8.1.15)
относительно
переменных
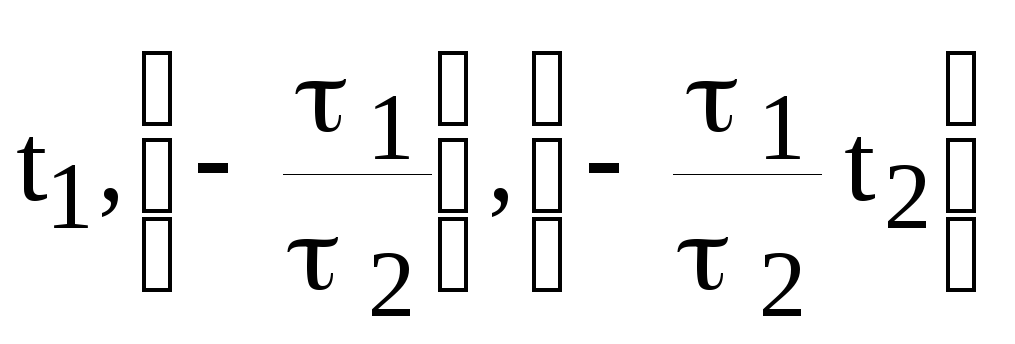 и
и
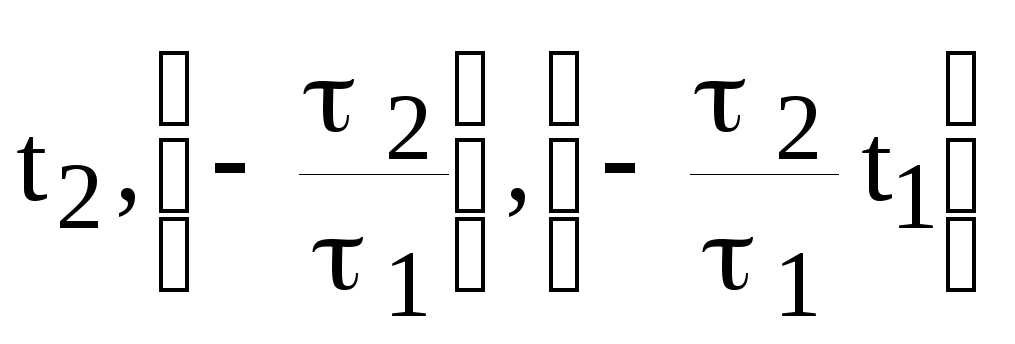 соответственно, которые будут иметь
единственное решение в случае линейной
независимости троек векторов
соответственно, которые будут иметь
единственное решение в случае линейной
независимости троек векторов
![]() и
и
![]() .
.
Таким
образом, для того чтобы через точку,
заданную вектором
![]() ,
можно было провести единственную прямую,
пересекающую две прямые
,
можно было провести единственную прямую,
пересекающую две прямые
![]() и
и
![]() ,
необходимо и достаточно, чтобы четверка
векторов
,
необходимо и достаточно, чтобы четверка
векторов
![]() была линейно зависима, а каждая из двух
троек
была линейно зависима, а каждая из двух
троек
![]() и
и
![]() оказалась линейно независима.
оказалась линейно независима.
Полагая,
например,
![]() ,
находим путем решения системы (8.1.14)
значения
,
находим путем решения системы (8.1.14)
значения
![]() и вычисляем по формулам (8.1.10), (8.1.11) точки
пересечения, а по формуле (8.1.13) направляющий
вектор искомой прямой.
и вычисляем по формулам (8.1.10), (8.1.11) точки
пересечения, а по формуле (8.1.13) направляющий
вектор искомой прямой.
Пример
2.
Найдите прямую, проходящую через точку,
заданную вектором
![]() и пересекающую прямые
и пересекающую прямые
![]() и
и
![]() ,
и найдите точки пересечения искомой
прямой с двумя данными прямыми, если
,
и найдите точки пересечения искомой
прямой с двумя данными прямыми, если
![]()
![]() .
.
Решение. Поскольку
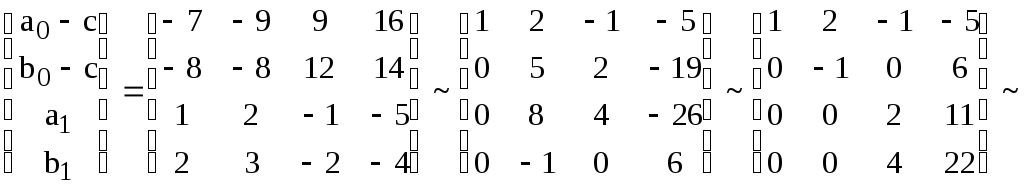
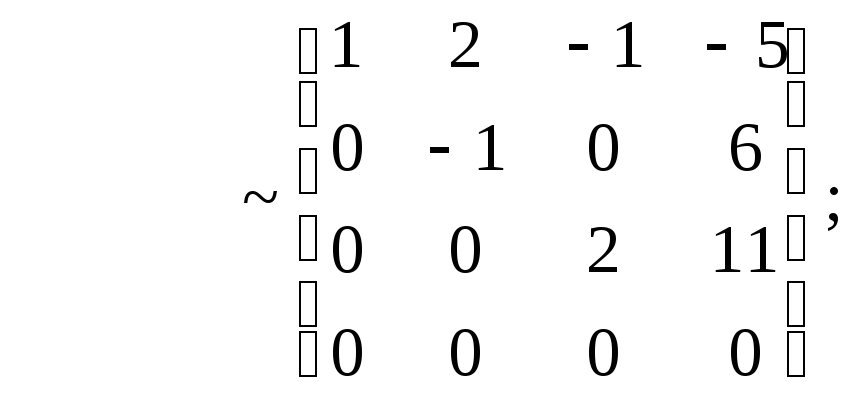
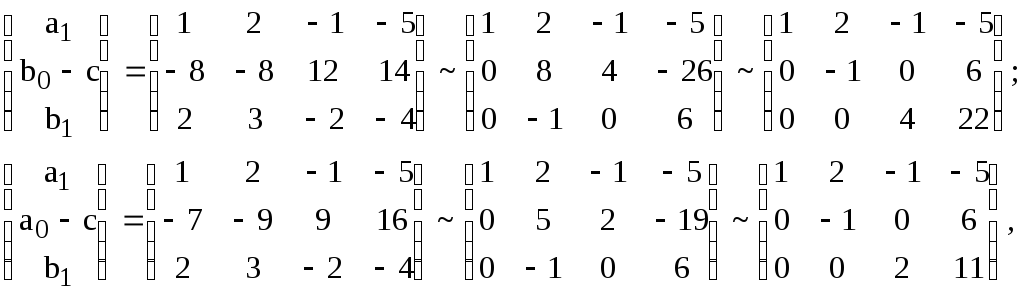
условия,
необходимые и достаточные для того,
чтобы через точку, заданную вектором
![]() ,
можно было провести прямую, пересекающие
две прямые
,
можно было провести прямую, пересекающие
две прямые
![]() и
и
![]() ,
выполнены. Составим и решим систему
(8.1.14):
,
выполнены. Составим и решим систему
(8.1.14):
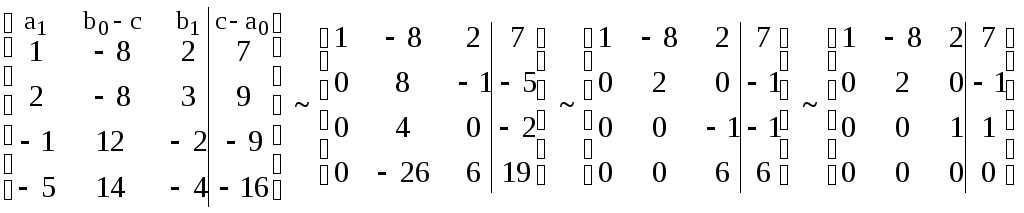 ,
,
т.е.
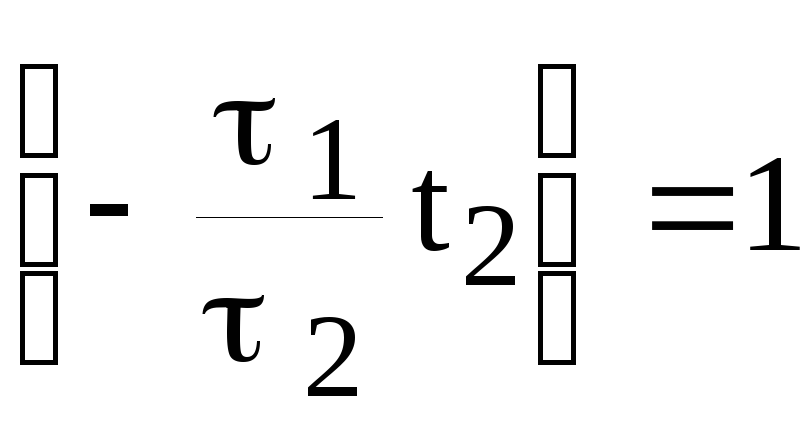 ,
,
 ,
,
![]() .
Положим
.
Положим
![]() .
Тогда
.
Тогда
![]() .
Следовательно,
координаты
направляющего
вектора
искомой
прямой
.
Следовательно,
координаты
направляющего
вектора
искомой
прямой
![]()
![]() ;
;
координаты точек пересечения
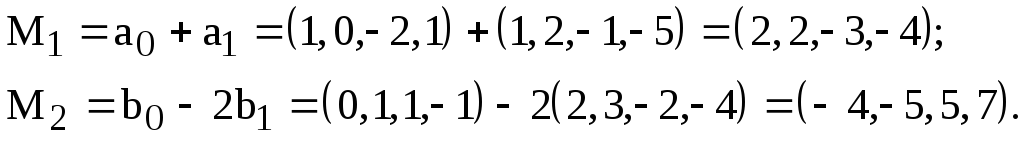
Проверка:
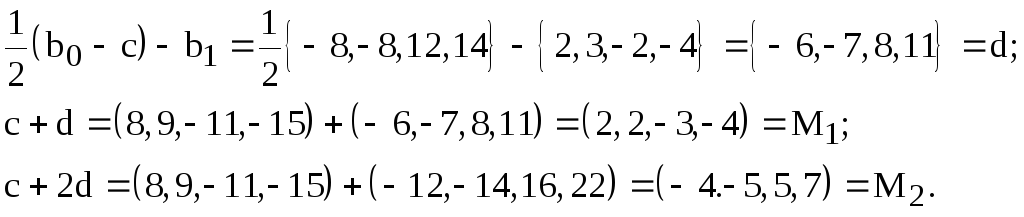
Пример
3.
Составьте уравнение прямых, проходящих
через точку
![]() и образующих с прямой
и образующих с прямой
![]() углы в
углы в
![]() .
.
Решение.
Выберем две точки
![]() и
и
![]() на прямой
на прямой
![]() .
Пусть
.
Пусть
![]() ,
,
![]() .
Тогда
направляющий
вектор
прямой
.
Тогда
направляющий
вектор
прямой
![]() .
Пусть
.
Пусть
![]() - направляющий вектор искомой прямой.
Тогда в соответствии с соотношением
(8.1.7)
- направляющий вектор искомой прямой.
Тогда в соответствии с соотношением
(8.1.7)
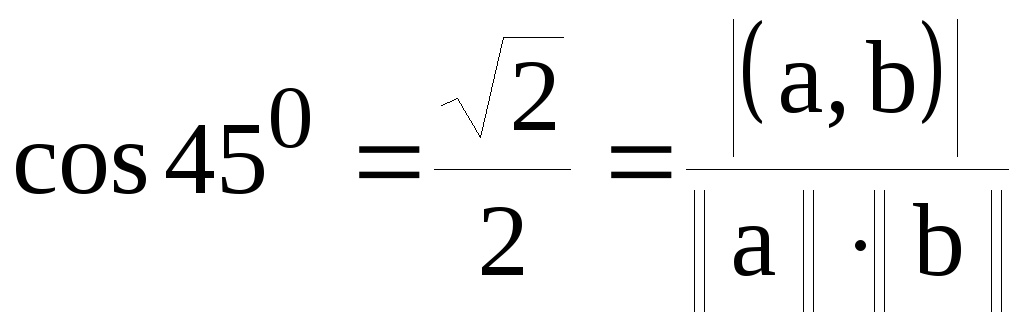 .
.
Считая систему координат прямоугольной, отсюда имеем:
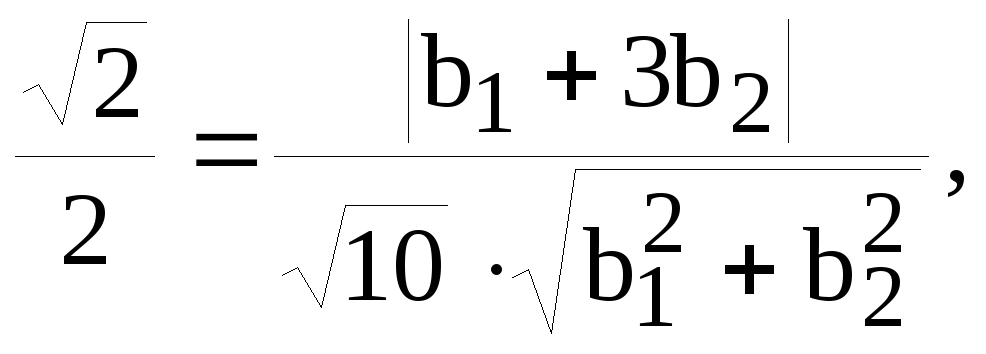
или
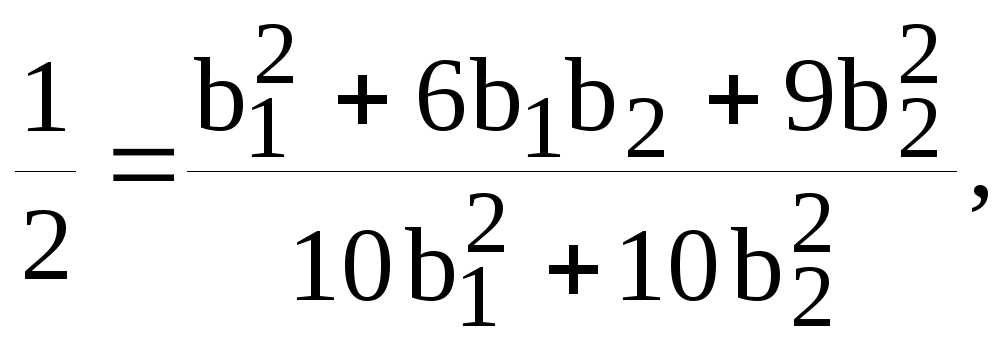
или
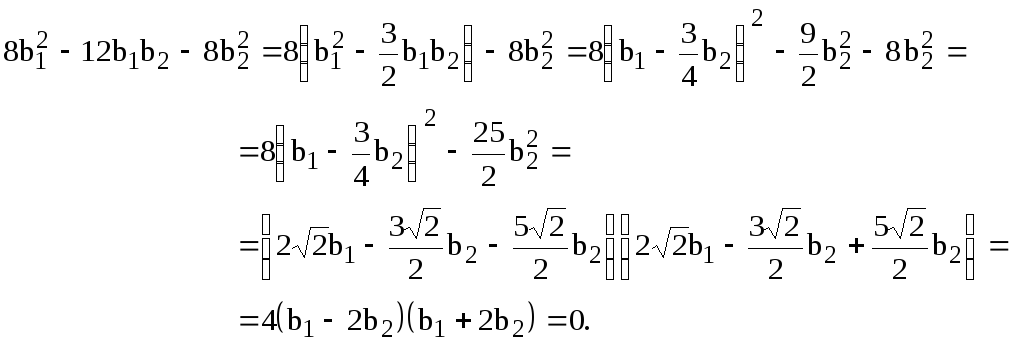
Следовательно,
![]() либо
либо
![]() .
Полагая
.
Полагая
![]() ,
получаем два направляющих вектора
,
получаем два направляющих вектора
![]() ,
,
![]() ,
что позволяет записать два канонических
уравнения
,
что позволяет записать два канонических
уравнения
![]() и
и
![]() .
.
В задачах, требующих вычисления скалярных произведений, предполагается, что система координат прямоугольная.
8.1.1. Составьте параметрические уравнения прямой, проходящей через две данные точки:
а)
![]() и
и
![]()
б)
![]() и
и
![]()
в)
![]() и
и
![]()
8.1.2. Составьте канонические и параметрические уравнения прямых, проходящих чрез точку:
а)
![]() параллельно прямой
параллельно прямой
![]()
б)
![]() параллельно вектору
параллельно вектору
![]()
в)
![]() параллельно прямой
параллельно прямой
![]()
г)
![]() параллельно ее радиус - вектору.
параллельно ее радиус - вектору.
8.1.3. Даны две прямые. Установите, пересекаются они, скрещиваются, параллельны или совпадают. Если прямые пересекаются, найдите координаты точки их пересечения. Прямые заданы уравнениями:
а)
![]() и
и
![]()
б)
![]() и
и
![]()
8.1.4.
При каких
![]() прямые
прямые
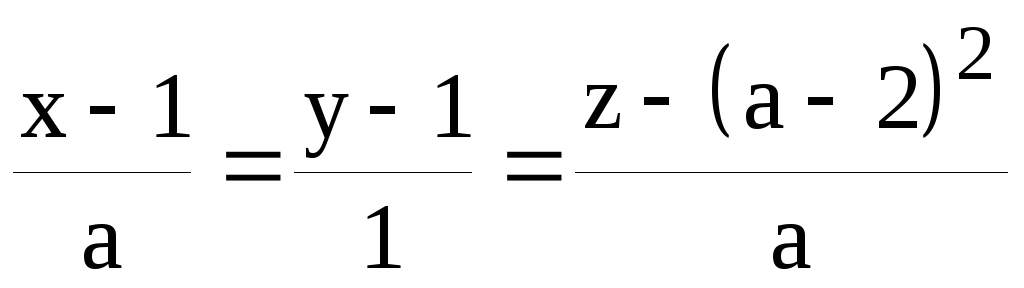 и
и
![]()
а) пересекаются;
б) скрещиваются;
в) параллельны;
г) совпадают?
8.1.5.
Составьте параметрические уравнения
прямой, проходящей через точку
![]() и пересекающей две данные прямые:
и пересекающей две данные прямые:
а)![]()
![]() и
и
![]()
б)
![]()
![]() и
и
![]()
в)
![]()
![]() и
и
![]() .
.
8.1.6.
Найдите прямую, проходящую через точку,
заданную вектором
![]() и пересекающую прямые
и пересекающую прямые
![]() и
и
![]() ,
и найдите точки пересечения искомой
прямой с двумя данными прямыми, если
,
и найдите точки пересечения искомой
прямой с двумя данными прямыми, если
![]()
![]() .
.
8.1.7.
Найдите точку пересечения двух прямых
![]() и
и
![]()
а)
![]()
![]()
б)
![]()
![]() .
.
8.1.8.
На прямой
![]() найдите точку
найдите точку
![]() ,
сумма расстояний от которой до точек
,
сумма расстояний от которой до точек
![]() и
и
![]() минимальна.
минимальна.
8.1.9.
На прямой
![]() найдите точку, равноудаленную от точек
найдите точку, равноудаленную от точек
![]() и
и
![]() .
.
8.1.10.
Точка
![]() лежит на прямой
лежит на прямой
![]() ,
причем
,
причем
![]() равноудалена от точек
равноудалена от точек
![]() и
и
![]() .
Найдите координаты точки
.
Найдите координаты точки
![]() .
.
8.1.11.
Составьте уравнение прямой, пересекающей
две прямые
![]() и
и
![]() и
параллельной
прямой
и
параллельной
прямой
![]()
![]() .
.
8.1.12. Найдите угол между прямыми:
а)
![]() и
и
![]() ;
;
б)
![]() и
и
![]() .
.
8.1.13.
Даны точка
![]() и прямая
и прямая
![]() .
Вычислите расстояние от точки
.
Вычислите расстояние от точки
![]() до прямой
до прямой
![]() ;
найдите координаты проекции точки
;
найдите координаты проекции точки
![]() на
на
![]() и координаты точки
и координаты точки
![]() ,
симметричной
,
симметричной
![]() относительно
относительно
![]() ;
составьте уравнение прямой, проходящей
через точку
;
составьте уравнение прямой, проходящей
через точку
![]() и пересекающей данную прямую под прямым
углом (“опустите перпендикуляр” из
точки
и пересекающей данную прямую под прямым
углом (“опустите перпендикуляр” из
точки
![]() на
на
![]() ).
Прямая
).
Прямая
![]() задана уравнениями:
задана уравнениями:
а)
![]()
б)
![]() .
.
8.1.14.
Найдите точку, симметричную точке
![]() относительно прямой
относительно прямой
![]() .
.
8.1.15.
На прямой
![]() найдите точку, ближайшую к точке
найдите точку, ближайшую к точке
![]() .
.
8.1.16. Найдите расстояние между прямыми:
а)
![]() и
и
![]()
